Эта работа ждет рассмотрения преподавателем
Дата последней правки страницы: 02.11.2016
Авторы этой статьи считают, что задание выполнено.

Авторы описания: Гурьянов Алексей Константинович, Кибитова Валерия Николаевна

Оба автора внесли в данную статью равноценный вклад. Сбор информации, построение алгоритмов, а также составление данной статьи происходило совместно обоими авторами, четкого распределения ответственности произвести невозможно.

Алгоритм кластеризации, основанный на минимальном остовном дереве
Последовательный алгоритм
Последовательная сложность	[math]O(N^2 \log_2 N)[/math]
Объём входных данных	[math] O(Nm) [/math]
Объём выходных данных	[math] O(N) [/math]

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм решает задачу кластеризации. Кластеризация – это задача разбиения множества объектов на не пересекающиеся подмножества, называемые кластерами таким образом, что объекты в одном кластере были более похожи (в каком-либо смысле) друг на друга, а объекты в разных кластерах существенно отличались.

В отличии от классических алгоритмов кластеризации, данный алгоритм не предполагает, что кластеры являются сферической формы, и способен выделять кластеры произвольной формы. Данный алгоритм применяется в кластеризации цветов в различных изображениях, например, таких как: фотографии, карты, коммерческой рекламе, а также в различных биологических изображениях.

Проблема нахождения минимального остовного дерева, а также ее решение было предложено Борувка в 1926 году. Идея использовать минимальное остовное дерево для кластеризации впервые была предложена Zahn в 1971^[1], в последующие годы данная идея развивалась такими учеными как: Asano, Bhattacharya, Keil, и Yao^[2], Avis^[3], Eldershaw и Hegland^[4], Paivinen и другими^[5].

Основная идея алгоритма состоит из следующих шагов:

1. Построение взвешенного неориентированного графа по исходным данным следующим образом. Каждый объект в заданном множестве представляется вершиной в графе, а ребро между двумя вершинами представляет собой расстояние между объектами, которое определяется по выбранной метрике.

2. Построение минимального остовного дерева. Для этого можно использовать следующие алгоритмы:

алгоритм Крускала;
алгоритм Прима;
алгоритм Борувки.

3. Выделение кластеров. В минимальном остовном дереве, выбирается [math]k-1[/math] ребро (где [math]k[/math] – это заранее определенное число кластеров), имеющие наибольшой вес. Выбранные ребра удаляются. Оставшиеся k компонент связности считаются кластерами.

В данной статье алгоритм будет описываться с использованием алгоритма Борувки. Подробное описание которого можно найти пройдя по ссылке [Алгоритм Борувки]

Общая идея его состоит в следующем:

Изначально каждая вершина графа — тривиальное дерево, а ребра не принадлежат никакому дереву.
Для каждого дерева найдем минимальное по весу инцидентное ему ребро. Добавим все такие ребра.
Повторяем шаг 2 пока в графе не останется только одно дерево.

1.2 Математическое описание алгоритма

На вход алгоритму подается набор [math]N[/math] векторов размерности [math]m[/math] : [math](a_{i,1}, a_{i,2}, ..., a_{i,m})[/math], где [math] a_j \in \mathbb {R} \quad \forall j \in [1,m], i \in [1..N] [/math] и количество кластеров [math]K[/math], на которые необходимо разбить множество точек.

На выход алгоритм должен вывести [math]N[/math] чисел от [math]1[/math] до [math]K[/math], показывающих принадлежность входных векторов кластерам.

1.2.1 Основные обозначения

[math]E[/math] - множество рёбер.
[math]V[/math] - множество вершин.
[math]G = (V,E) [/math] - неориентированный граф, заданный множеством вершин [math]V[/math] и множеством рёбер [math]E[/math]
[math]MST(G)[/math] (Minimum Spanning Tree) - минимальное остовное дерево графа [math][/math]. Остовное дерево — ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины. Минимальное остовное дерево в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

1.2.2 Функция веса

Для решения задачи допускаются различные функции веса, используемые для построения минимального основного дерева. Подобные функции будут влиять на структура построенных кластеров и могут меняться в соответствии с требованиями к решению.

В данной статье будет рассматриваться евклидова метрика:

[math] | x , y | = \sqrt{\sum_i^m (x_i - y_i)^2} [/math]

1.3 Вычислительное ядро алгоритма

Работу алгоритма можно разделить на три блока:

1: Вычисление расстояний между вершинами и заполнение данных о компонентах связности
2: Построение минимального основного дерева
3: Разделение на K кластеров

Из них основное время работы алгоритма занимают блоки 1 и 2.

1.4 Макроструктура алгоритма

В алгоритме используются следующие структуры данных:

Node – структура данных, описывающая вершину пространства. Включает в себя значения координат точки.
Edge – структура данных, описывающая узел между двумя вершинами. Включает в себя индексы двух вершин и расстояние между ними
Components – класс, описывающий состояние компонент связности в промежуточных состояниях графа по мере добавления в него ребер. Включает в себя информацию о том, какой компоненте связности принадлежит каждая точка и о расстоянии между каждой парой компонент связности, которая равна минимальному ребру между двумя вершинами в этих двух компонентах.

Для описания алгоритма вводятся следующие макрооперации:

1: getDistance – находит расстояние между двумя вершинами графа как расстояние между соответствующими им точками пространства. (Сложность – [math]O(m)[/math])
2: initializeComponents – инициализирует состояние класса Components информацией о вершинах и ребрах. В каждую исходную компоненту связности входит одна вершина. (Сложность – [math]O(N^2)[/math])
3: findMinimalOutgoingEdge – находит ребро c наименьшей длиной, исходящее из заданной компоненты связности. (Cложность – [math]O(N)[/math])
4: findComp – возвращает индекс компоненты связности в которой находится вершина (Cложность – [math]O(1)[/math])
5: connectComponentsWithEdge – соединяет две компоненты связности, связанные поданным на вход ребром. Объединение компонент включает в себя замену ребер инцидентности новой компоненты на минимальные ребра из пары объединяемых компонент. (Сложность – [math]O(N)[/math])

Макрооперации 2-5 относятся к последовательной реализации алгоритма Борувки, который был выбран как основа вычислительного ядра алгоритма.

1.5 Схема реализации последовательного алгоритма

Схема работы алгоритма была создана с учетом последующей параллельной реализации,^[6]

int N;        // Размер входных данных
int number_of_clusters;        // Число кластеров
int size = N*N;        // Размер матрицы инцидентности
Node nodes[N];        // Вершины(точки), заданные начальными условиями
Edge edges[size];        // Все расстояния между вершинами 
vector<Edge> tree;        // Рёбра минимального остовного дерева
Components comps;         // Структура компонент связности
read_data(&nodes, file_name);    // Считывание начальных данных

//----------------Вычисление расстояний между вершинами----------------//
for(int i = 0; i < N-1; i++) {
    for(int j = i+1; j < N; j++) {
        double distance = getDistance(node[i], node[j]);        // Вычисление расстояний между вершинами
	edges[i*N + j] = Edge(i,j,distance);        // Запись значения расстояния в массив
        edges[j*N + i] = Edge(i,j,distance);        // Запись значения расстояния в массив
    }
}

//----------------Заполнение данных о компонентах связности--------------//
initializeComponents(&comps, nodes, edges); 

//----------------Построение минимального основного дерева--------------//
while(comps.size > 1) {
    vector<edges> mstedges;
    for component in comps {
        edge e = findMinimalOutgoingEdge(component, comps, edges) // Нахождение минимального ребра инцидентного данной компоненте
        mstedges.add(e)
    }
    for mstedge in mstedges {
        if (findComp(comps, mstedge.first) != findComp(comps, mstedge.second)) { 
             connectComponentsWithEdge(comps, mstedge) // Объединение двух компонент
             tree.add(mstedge) // Добавление ребра в минимальное основное дерево
        }
    } 
}

//-----------------------Разделение на K кластеров--------------------------//
sort(tree)
for(int i = tree.size() - 1; i > tree.size() - 1 - number_of_clusters; i--) {
    remove_edge(tree, i);        // Удаление самых длинных рёбер из MST - формирование кластеров
}
write_data(tree);        // Запись выходных данных

1.6 Последовательная сложность алгоритма

Среди выделенных в описании частей алгоритма, самую большую сложность для оценивания временной сложности вызывает часть 3, являющаяся реализацией алгоритма Борувки. Однако если заметить, что после выполнения каждого тела внешнего цикла количество компонент связности будет уменьшаться как минимум вдвое (так как одно ребро в списке ребер минимального основного дерева может повториться максимум двое), то можно сделать вывод, что сложность в худшем случае этого блока алгоритма является [math] O (N^2 \log_2 N) [/math].

Асимптотическую сложность алгоритма можно выразить как сумму временных сложностей четырех выделенных в описании частей:

[math] TC(N, m) = O(N^2m) + O(N^2) + O(N^2 \log_2 N) + O(N \log_2 N) = O(N^2 (m + \log_2 N)) [/math]

Если посчитать размерность пространства входных точек за константу при расчете сложности, то временная сложность выразится как

[math] TC(N, m) = O(N^2 \log_2 N) [/math]

При дальнейшем обсуждении свойств алгоритма размерность пространства входных точек будет приниматься за константу.

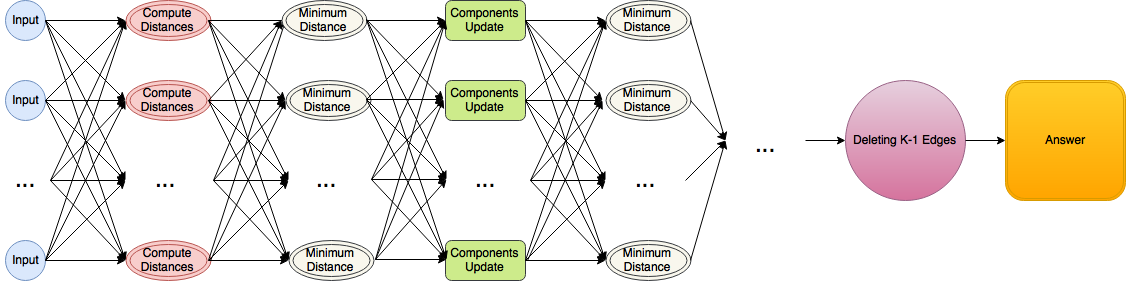
1.7 Информационный граф

Информационный граф параллельного алгоритма кластеризации на основе алгоритма Борувки

В то время как узлы каждого слоя не зависят информационно от каждого узла предыдущего слоя, из-за того что структура информационного графа определяется динамически по ходу действия программы (на основе выбора ребер, по которым будет проводится слияние компонент связности), составить информационный граф, использующий более разреженную структуру связей между слоями, не представляется возможным.

1.8 Ресурс параллелизма алгоритма

Данная задача хорошо параллелизуется благодаря тому, что наиболее требующие вычислительных ресурсов блоки алгоритмического ядра алгоритма можно эффективно разделить по процессам. Процесс считывания входных данных и процесс расчета расстояния между точками, которые представляет собой большое количество попарных взятий евклидова расстояния, можно выполнить за [math]O(1)[/math] при наличии как минимум [math] N^2 [/math] процессоров.

Основная особенность алгоритма построения минимального основного дерева Борувки состоит в том, что основной блок этого алгоритма, нахождения минимального ребра, инцидентного заданной вершине, можно проводить независимо. Это позволяет провести вычисления в ярусе, ответственном за поиск кратчайших ребер за [math]O(1)[/math] времени при наличии как минимум [math]N^3[/math] процессоров. Процесс обновления информации о компонентах связности, который заключается в обновлении индексов кластеров вершин и в обновлении расстояний между кластерами, можно представить в виде независимой последовательности операций взятия минимума и операций присваивания в количестве [math]O(N)[/math] штук (количество компонент связности), что позволит выполнить ярус, ответственный за обновление структуры компонент связности за [math]O(1)[/math] при наличие как минимум [math]2N[/math] процессоров. Это значит, что каждый ярус будет выполняться за [math] O(1) [/math] времени, и аналогично последовательному алгоритму Борувки, после выполнения 2 ярусов количество компонент связности уменьшится минимум вдвое, что гарантирует то, что за время выполнения алгоритма повторится не более чем [math] 4 * \log_2 N [/math] ярусов. Учитывая ярусы, посвященные считыванию ввода, вычислению расстояний между точками пространства, удалению [math]K-1[/math] ребер из минимального опорного дерева и выводу ответа, итоговую параллельная сложность алгоритма можно оценить как [math] 2 * \log_2 N + 5[/math].

В терминах свойств параллелизма, в описываемом алгоритме решения задачи присутствует конечный параллелизм на уровне одного яруса нахождения кратчайшего инциндентного ребра и на уровне одного яруса обновления структуры компонент связности. Массовый параллелизм в предложенном алгоритме отсутствует.

1.9 Входные и выходные данные алгоритма

1.9.1 Входные данные алгоритма

На вход алгоритму подается набор [math]N[/math] векторов размерности [math]m[/math] : [math](a_{i,1}, a_{i,2}, ..., a_{i,m})[/math], где [math] a_j \in \mathbb {R} \quad \forall j \in [1,m], i \in [1..N] [/math] и количество кластеров [math]K[/math], на которые необходимо разбить множество точек. Общий объем входных данных можно оценить как [math]O(Nm)[/math].

Если оценивать размерность пространства входных точек константой, то объем входных данных можно оценить как [math]O(N)[/math].

1.9.2 Выходные данные алгоритма

На выход алгоритм должен вывести [math]N[/math] чисел от [math]1[/math] до [math]K[/math], показывающих принадлежность входных векторов кластерам. Общий объем входных данных можно оценить как [math]O(N)[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности алгоритма равно [math] \frac{N^2 \log_2 N} {\log_2 N} = N^2 [/math].

Вычислительную мощность алгоритма можно оценить как [math] \frac {N^2 \log_2 N} {N} = N \log_2 N[/math].

Алгоритм устойчив к сохранению погрешностей, так как в алгоритме нет необходимости производить последовательные арифметические операции (за исключеним единоразового расчета попарных расстояний между точками), а операция взятия минимума двух чисел не создает ошибок.

Алгоритм полностью детерминирован в предположении что расстояния между каждой парой точек различны. Если существуют точки, расстояния между которыми одинаковы, то на этапе выбора кратчайшего инцидентного вершине ребра может возникать неопределенность, которую, однако, можно преодолеть уточнив выбор кратчайшего из набора ребер как ребро с минимальной длиной, ребро с наименьшим минимальным индексом вершины ребра при равенстве длин, или ребро с наименьшим максимальным индексом вершины ребра при равенстве минимального индекса вершин. Так как при совпадении минимального и максимального индекса вершин ребра совпадают, то проблем с упорядочиванием такой пары ребер возникнуть не может.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Существующих реализаций алгоритма кластеризации в настоящий момент немного. Ниже приводится список некоторых из них:

MST Clustering Python

Однако существует множество реализаций алгоритма поиска минимального остовного дерева, на основе которых можно реализовать алгоритм кластеризации.

3 Литература

↑ Zahn C. T. Graph-theoretical methods for detecting and describing gestalt clusters //IEEE Transactions on computers. – 1971. – Т. 100. – №. 1. – С. 68-86.
↑ Asano T. et al. Clustering algorithms based on minimum and maximum spanning trees //Proceedings of the fourth annual symposium on Computational geometry. – ACM, 1988. – С. 252-257.
↑ Avis D. Diameter partitioning //Discrete & Computational Geometry. – 1986. – Т. 1. – №. 3. – С. 265-276.
↑ Eldershaw C., Hegland M. Cluster analysis using triangulation //Computational Techniques and Applications. – 1997. – С. 201-208.
↑ Grygorash O., Zhou Y., Jorgensen Z. Minimum spanning tree based clustering algorithms //2006 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI'06). – IEEE, 2006. – С. 73-81.
↑ Chung S., Condon A. Parallel implementation of Bouvka's minimum spanning tree algorithm //Parallel Processing Symposium, 1996., Proceedings of IPPS'96, The 10th International. – IEEE, 1996. – С. 302-308.

[1] Zahn C. T. Graph-theoretical methods for detecting and describing gestalt clusters //IEEE Transactions on computers. – 1971. – Т. 100. – №. 1. – С. 68-86.

[2] Asano T. et al. Clustering algorithms based on minimum and maximum spanning trees //Proceedings of the fourth annual symposium on Computational geometry. – ACM, 1988. – С. 252-257.

[3] Avis D. Diameter partitioning //Discrete & Computational Geometry. – 1986. – Т. 1. – №. 3. – С. 265-276.

[4] Eldershaw C., Hegland M. Cluster analysis using triangulation //Computational Techniques and Applications. – 1997. – С. 201-208.

[5] Grygorash O., Zhou Y., Jorgensen Z. Minimum spanning tree based clustering algorithms //2006 18th IEEE International Conference on Tools with Artificial Intelligence (ICTAI'06). – IEEE, 2006. – С. 73-81.

[6] Chung S., Condon A. Parallel implementation of Bouvka's minimum spanning tree algorithm //Parallel Processing Symposium, 1996., Proceedings of IPPS'96, The 10th International. – IEEE, 1996. – С. 302-308.

[1]

[2]

[3]

[4]

[5]

[6]

Участник:Guryanovak/Алгоритм кластеризации, основанный на минимальном остовном дереве