Участник:Oleggium/Метод Ньютона для решения систем нелинейных уравнений(2)

Эта работа прошла предварительную проверку Дата последней правки страницы: 07.11.2016 Данная работа соответствует формальным критериям. Проверено VadimVV.

Метод Ньютона
Последовательный алгоритм
Последовательная сложность	[math]O(k \cdot n^3)[/math] в случае решения СЛАУ методом Гаусса
Объём входных данных	[math]F(x)[/math] - [math]n[/math] [math]n[/math]-мерных функций (так же дополнительно могут быть даны [math]n^2[/math] производных), [math]n[/math]-мерный вектор [math]x^0[/math] - начальное приближение, [math]\varepsilon[/math] - точность
Объём выходных данных	[math]n[/math]-мерный вектор

Авторы: Гирняк О.Р., Васильков Д.А. (все пункты выполнялись совместно).

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Ньютона для решение систем нелинейных уравнений - обобщение классического метода Ньютона (метода касательных) нахождения корня (нуля) заданной функции. Одномерный метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений [math]x_{n}[/math] вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

1.2 Математическое описание алгоритма

Рассмотрим систему нелинейных уравнений

[math]F(x) = 0, F(x), x \in \mathbb{R}^{n}, (1)[/math]

и предположим, что существует вектор [math]\bar{x} \in D \subset \mathbb{R}^{n}[/math], являющийся решением системы (1).

Будем считать, что [math]F(x) = (f_1(x), f_2(x), ... f_n(x))^T[/math], причем [math]f_i(\cdot) \in C^1(D) \forall i[/math].

Разложим [math]F(x)[/math] в окрестности точки [math]\bar{x}: F(x) = F(x^0) + F'(x^0)(x-x^0) + o(||x-x^0||)[/math].

Здесь [math] F'(x) = \frac{\partial{F(x)}}{\partial{x}} = \begin{pmatrix} \frac{\partial{f_1(x_1)}}{\partial{x_1}} & \frac{\partial{f_1(x_2)}}{\partial{x_2}} & \cdots & \frac{\partial{f_1(x_n)}}{\partial{x_n}}\\ \frac{\partial{f_2(x_1)}}{\partial{x_1}} & \frac{\partial{f_2(x_2)}}{\partial{x_2}} & \cdots & \frac{\partial{f_2(x_n)}}{\partial{x_n}}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial{f_n(x_1)}}{\partial{x_1}} & \frac{\partial{f_n(x_2)}}{\partial{x_2}} & \cdots & \frac{\partial{f_n(x_n)}}{\partial{x_n}} \end{pmatrix} [/math]

называется матрицей Якоби, а её определитель – якобианом системы (1).

Исходное уравнение заменим следующим: [math]F(x^0) + F'(x^0)(x-x^0) = 0[/math]. Считая матрицу Якоби [math]F'(x^0)[/math] неособой, разрешим это уравнение относительно [math]x: x = x^0 - [F'(x)]^{-1}F(x^0)[/math]. И вообще положим

[math]x^{k+1} = x^{k} - [F'(x^k)]^{-1}F(x^k)[/math].

При сделанных относительно [math]F(\cdot)[/math] предположениях имеет место сходимость последовательности [math]x^{k}[/math] к решению системы со скоростью геометрической прогрессии при условии, что начальное приближение [math]x^0[/math] выбрано из достаточно малой окрестности решения [math]\bar{x}[/math].

При дополнительном предположении [math]F(\cdot) \in C^2[/math] имеет место квадратичная сходимость метода, т. е.

[math]||x^{k+1}-\bar{x}|| \le \omega||x^{k}-\bar{x}||^2[/math].

Сформулируем теорему.

Теорема. Пусть в некоторой окрестности решения [math]\bar{x}[/math] системы (1) функции [math]f_i(\cdot) \in C^2[/math] и якобиан системы отличен от нуля в этой окрестности. Тогда существует [math]\delta[/math]-окрестность точки [math]\bar{x}[/math] такая, что при любом выборе начального приближения [math]x^0[/math] из этой окрестности последовательность [math]{x_k}[/math] не выходит из неё и имеет место квадратичная сходимость этой последовательности.

Замечание 1. В качестве критерия окончания процесса итераций обычно берут условие: [math]||x^{k+1}-x^k|| \lt \varepsilon[/math].

Замечание 2. Сложность метода Ньютона – в обращении матрицы Якоби. Вводя обозначение [math]\Delta x^k = x^{k+1}-x^k[/math], получаем для вычисления [math]\Delta x^k[/math] СЛАУ

[math]\frac{\partial F(x^k)}{\partial x} \cdot \Delta x^k = -F(x^k)[/math],

откуда и находим искомую поправку [math]\Delta x^k[/math], а затем и следующее приближение [math]x^{k+1} = x^k + \Delta x[/math] к решению [math]\bar{x}[/math]. Очевидно, что это значительно сокращает количество арифметических операций для построения очередного приближения.

Замечание 3. Начиная с некоторого шага [math]k_0[/math] решают стационарную СЛАУ

[math]\frac{\partial F(x^{k_0})}{\partial x} \cdot \Delta x^k = -F(x^k)[/math],

Данное видоизменение носит название модифицированный метод Ньютона.

Замечание 4. (О выборе начального приближения). Пусть вектор-функция [math]\Phi(\lambda, x)[/math] такова, что [math]\Phi(1, x) = F(x)[/math], а система [math]\Phi(0, x) = 0[/math] может быть решена. Тогда разбивая [math][0,1][/math] на [math]N[/math] частей решают методом Ньютона набор из [math]N[/math] систем [math]\Phi(i/N, x) = F(x), i = 1,... N[/math], принимая для каждой следующей системы в качестве начального приближения решение предыдущей системы.

1.3 Вычислительное ядро алгоритма

Вычислительными ядрами данного алгоритма являются:

- Численное вычисление Якобиана(в случае, если производные не даны) [math]\frac{\partial F(x^k)}{\partial x} [/math].

- Решение СЛАУ(например, методом Гаусса) [math]\frac{\partial F(x^k)}{\partial x} \cdot \Delta x^k = -F(x^k)[/math].

1.4 Макроструктура алгоритма

Как уже было описано в вычислительном ядре, данный алгоритм использует 2 основных метода - решение СЛАУ и вычисление Якобиана.

1.5 Схема реализации последовательного алгоритма

Построим математическое описание нашего алгоритма.

Входные данные:[math]F(x)[/math] - [math]n[/math] [math]n[/math]-мерных функций; [math]n[/math]-мерный вектор [math]x^0[/math] - начальное приближение. [math]\varepsilon[/math] - точность.

---

[math]rezult = x^0[/math];

[math]k = 0[/math] - номер итерации;

DO

Вычисляем [math]\frac{\partial F(x^k)}{\partial x} [/math] (если производные не даны, то их можно вычислить численно);

Вычисляем [math]F(x^k)[/math];

Решаем СЛАУ(например, методом Гаусса) [math]\frac{\partial F(x^k)}{\partial x} \cdot \Delta x^k = -F(x^k)[/math];

[math]result = result + \Delta x^k[/math];

WHILE [math]||\Delta x^k|| \gt \varepsilon[/math] AND [math]k \lt k_{max}[/math].

---

Выходные данные: [math]result[/math] - численное решение заданной нелинейной системы.

1.6 Последовательная сложность алгоритма

В оценке сложности будем учитывать только арифметические операции, сделанные в самом алгоритме. Однако, так же необходимо помнить о том, что внутри каждого вызова каждой из заданных нелинейных функций возможно выполнение большого количество арифметических операций. Не зная конкретный вид этих функций, получить оценку арифметических операций внутри функций невозможно. Очевидно, что при сложных нелинейных функциях, суммарное количество операций внутри функций и вне их, требующихся для вычисления Якобиана, может быть существенно больше сложности решения СЛАУ. В этом случае целесообразно использовать модифицированный метод Ньютона, о котором говорилось ранее.

Будем считать, что в цикле DO ... WHILE мы сделали [math]k[/math] итераций (то есть получили конечное решение, причем алгоритм сошелся к решению и была достигнута заданная точность). Количество итераций [math]k[/math] зависит от выбора начального приближения.

Каждая итерация состоит из следующего:

[math]\bullet[/math] Вычисление производных [math]\frac{\partial F(x^k)}{\partial x} [/math] в случае, если они не заданы. Для каждого дифференцирования используя, например, формулу центральной разностной производной [math]f'(x) = (f(x+h) - f(x-h))/2h [/math] необходимо 2 вызова функций, 3 сложения, одно умножение и одно деление. Количество арифметических операций - [math]5[/math]. Всего в матрице [math]n^2[/math] элементов. Получили сложность [math]O(5n^2)[/math] (если производные заданы, то необходимо сделать [math]n^2[/math] вызовов функций.

[math]\bullet[/math] Вычисляем [math]F(x^k)[/math] - [math]n[/math] вызовов функций.

[math]\bullet[/math] Решаем СЛАУ [math]\frac{\partial F(x^k)}{\partial x} \cdot \Delta x^k = -F(x^k)[/math] - В случае использования метода Гаусса [math]O(n^3)[/math].

В итоге получили сложность [math]O(k \cdot n^3)[/math].

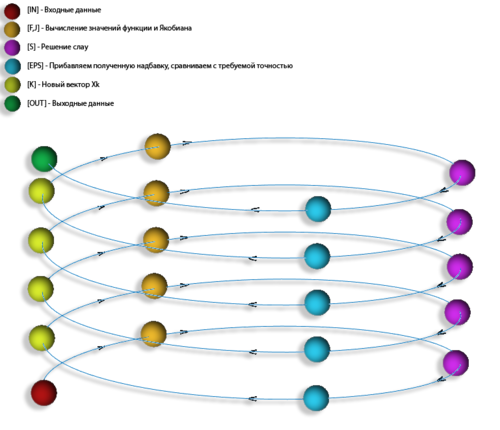
1.7 Информационный граф

Опишем информационный граф в виде рисунка:

Рис.1 Информационный граф алгоритма.

1.8 Ресурс параллелизма алгоритма

На каждой итерации алгоритма возможно использовать параллельное вычисление значений Якобиана(т.к. вычисление каждого значения в матрице не зависит от других), а так же параллельное решение СЛАУ. Пусть [math]p\lt n[/math] - количество потоков, вычислим параллельную сложность алгоритма без учета внутреннего вида заданных функций, а так же в предположении, что производные этих функций не даны:

[math]\bullet[/math] Вычисление производных [math]\frac{\partial F(x^k)}{\partial x} [/math] в случае, если они не заданы. Получили сложность [math]O(5n^2/p)[/math].

[math]\bullet[/math] Вычисляем [math]F(x^k)[/math] - [math]n[/math] вызовов функций.

[math]\bullet[/math] Решаем СЛАУ [math]\frac{\partial F(x^k)}{\partial x} \cdot \Delta x^k = -F(x^k)[/math] - В случае использования одной из параллельной реализации метода Гаусса сложность [math]O(n^3/p)[/math].

Итого получили сложность [math]O(n^3/p)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: [math]F(x)[/math] - [math]n[/math] [math]n[/math]-мерных функций (так же дополнительно могут быть даны [math]n^2[/math] производных), [math]n[/math]-мерный вектор [math]x^0[/math] - начальное приближение, [math]\varepsilon[/math] - точность.

Выходные данные: [math]n[/math]-мерный вектор [math]x^k[/math].

1.10 Свойства алгоритма

Сложность алгоритма очень сильно зависит от вида заданных нелинейных функций, от выбора способа решения СЛАУ, а так же от выбора начального приближения. При некорректном выборе начального приближения сходимости вообще может не быть. В разделах Математическое описание алгоритма и Последовательная сложность алгоритма представлены некоторые теоремы и утверждения, показывающие эти свойства. Вычислительную мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, в общем случае посчитать для данного алгоритма невозможно(ввиду того, что на вход алгоритму подаются и функции, и данные, причем функции произвольного вида).

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Поскольку для получения очередного приближения [math]x_k[/math], необходимо знать предыдущее, то эффективность и скорость алгоритма будут очень сильно зависеть от алгоритма, которым решается СЛАУ. Для решения СЛАУ существует огромное количество готовых библиотек для различных языков программирования. Их можно легко найти в интернете.

В качестве примера можно ознакомиться со следующими реализациями метода Ньютона:

• C++
• MATLAB
• MATLAB
• SAS

3 Литература

<references \>