Участник:Davletshuna Alexandra/Метод Якоби вычисления сингулярных чисел и векторов

Эта работа прошла предварительную проверку Дата последней правки страницы: 09.11.2016 Данная работа соответствует формальным критериям. Проверено ASA.

Метод Якоби вычисления сингулярных чисел и векторов
Последовательный алгоритм
Последовательная сложность	$O(n^3)$
Объём входных данных	$n^2$
Объём выходных данных	$2n^2 + n$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(n^2)$
Ширина ярусно-параллельной формы	$O(n)$

Авторы статьи: Давлетшина Александра (группа 619) пункты 1.1-1.4, 1.6, 2.7; Зайцева Александра (группа 601) пункты 1.5, 1.7-1.10, 2.7.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Сингулярным разложением называется разложение прямоугольной вещественной или комплексной матрицы, имеющее широкое применение, в силу своей наглядной геометрической интерпретации, при решении многих прикладных задач. Сингулярное разложение матрицы А позволяет вычислять сингулярные числа данной матрицы, а также, левые и правые сингулярные векторы матрицы А:

• левые сингулярные векторы матрицы А — это собственные векторы матрицы $AA^*$;

• правые сингулярные векторы матрицы A — это собственные векторы матрицы $A^*A$.

Геометрическая интерпретация сингулярного разложения заключается в следующем факте из геометрии: Образом любого линейного преобразования, заданного с помощью матрицы $m$x$n$, примененного к единичной сфере является гиперэллипсоид.

Из многочисленных разложений матриц, наиболее удобным является сингулярное разложение матрицы в виде: $A=U\Sigma V^*$, где $U, V$ – унитарные матрицы, а $\Sigma$ – диагональная матрица с вещественными положительными числами на диагонали .

Диагональные элементы матрицы $\Sigma$ называются сингулярными числами матрицы $A$, а столбцы матриц $U,V$ левыми и правыми сингулярными векторами соответственно.

Алгоритм Якоби сингулярного разложения матрицы был предложен одним из первых в 1846 году. Он приводит прямоугольную матрицу к диагональной матрице с помощью последовательности элементарных вращений. Метод может найти все сингулярные значения с очень высокой точностью. Однако его производительность является довольно низкой, в сравнении с конкурирующими методами.

Неявный метод Якоби математически эквивалентен применению метода Якоби вычисления собственных значений к матрице $A = G^TG$. Это значит, что на каждом шаге вычисляется вращение Якоби $J$, с помощью которого матрица $G^TG$ неявно пересчитывется в $J^TG^TGJ$; вращение выбрано так, чтобы пара внедиагональных элементов из $G^TG$ обратилась в нули в матрице $J^TG^TGJ$. При этом ни $G^TG$, ни $J^TG^TGJ$ не вычисляются в явном виде; вместо них вычисляется матрица $GJ$. Поэтому алгоритм называется методом односторонних вращений.

1.2 Математическое описание алгоритма

Исходные данные: матрица $G$ (элементы $g_{ij}, i, j = 1, \ldots, n$).

Вычисляемые данные: матрица $\Sigma = diag(\sigma_{i})$, где $\sigma_{i}$ - сингулярные числа, $U$ - матрица левых сингулярных векторов, $V$ - матрица правых сингулярных векторов.

симметричную матрицу $A = (G^TG)$ можно привести к диагональному виду: $RG^TGR^T$, где

$R(j,k,\theta) = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix}$ $\begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix}$

Обозначим $s = \sin \theta$ и $c = \cos \theta$.

Перемножив матрицы $RG^TGR^T$, получим следующие выражения:

$\begin{align} a_{jj}^{(i+1)} &= c^2\, a_{jj}^{(i)} - 2\, s c \,a_{jk}^{(i)} + s^2\, a_{kk}^{(i)} \\ a_{kk}^{(i+1)} &= s^2 \,a_{jj}^{(i)} + 2 s c\, a_{jk}^{(i)} + c^2 \, a_{kk}^{(i)} \\ a_{jk}^{(i+1)} &= a_{kj}^{(i+1)} = (c^2 - s^2 ) \, a_{jk}^{(i)} + s c \, (a_{kk}^{(i)} - a_{jj}^{(i)} ) \\ a_{jm}^{(i+1)} &= a_{mj}^{(i+1)} = c \, a_{jm}^{(i)} - s \, a_{km}^{(i)} & m \ne j,k \\ a_{km}^{(i+1)} &= a_{mk}^{(i+1)} = s \, a_{jm}^{(i)} + c \, a_{km}^{(i)} & m \ne j,k \\ a_{ml}^{(i+1)} &= a_{ml}^{(i)} &m,l \ne j,k \end{align}$

Т.к внедиагональные элементы должны быть равны 0, то выбираем $\theta$ так, чтобы $a_{jk}^{(i+1)} = 0$ и $a_{kj}^{(i+1)} = 0$.

Тогда решая уравнение получаем, что

$\begin{align} \tau &= {a_{jj} - a_{kk}}/{2a_{jk}} \\ t &= {sign(\tau)}/(|\tau| + \sqrt{1 + \tau^2}) \\ c &= 1/(\sqrt{1 + t^2}) \\ s &= ct \\ \end{align}$

Остановка вычислений алгоритма наступает, когда внедиагональные элементы становятся меньше некоторого наперед заданного числа $\varepsilon$.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляет непосредственно вычисление одностороннего вращения Якоби, т.е. вычисление элементов матрицы $g_{jm}^{(i+1)} = g_{mj}^{(i+1)}$ и $g_{km}^{(i+1)} = g_{mk}^{(i+1)}$, $m \ne j,k$, а также вычисления элементов $g_{jj}^{(i+1)}$ и $g_{kk}^{(i+1)}$, получившихся после умножения промежуточной матрицы на матрицу вращений Якоби:

$\begin{align} g_{jj}^{(i+1)} &= c^2\, g_{jj}^{(i)} - 2\, s c \,g_{jk}^{(i)} + s^2\, g_{kk}^{(i)} \\ g_{kk}^{(i+1)} &= s^2 \,g_{jj}^{(i)} + 2 s c\, g_{jk}^{(i)} + c^2 \, g_{kk}^{(i)} \\ g_{jk}^{(i+1)} &= g_{kj}^{(i+1)} = (c^2 - s^2 ) \, g_{jk}^{(i)} + s c \, (g_{kk}^{(i)} - g_{jj}^{(i)} ) \\ g_{jm}^{(i+1)} &= g_{mj}^{(i+1)} = c \, g_{jm}^{(i)} - s \, g_{km}^{(i)} & m \ne j,k \\ g_{km}^{(i+1)} &= g_{mk}^{(i+1)} = s \, g_{jm}^{(i)} + c \, g_{km}^{(i)} & m \ne j,k \\ g_{ml}^{(i+1)} &= g_{ml}^{(i)} &m,l \ne j,k \end{align}$

1.4 Макроструктура алгоритма

Основную часть метода составляет процедура односторонних вращений матрицы, которая в свою очередь состоит из:

1. Вычисление $\tau, c, s, t$.
2. Одностороннее вращение матрицы.

Что требует $O(n)$ операций.

После этого необходимо:

1. Вычислить сингулярные числа $\sigma_i$. Что требует $O(n)$ операций.
2. Вычислить $U$ и $V$. Что требует $O(n^2)$ операций.

1.5 Схема реализации последовательного алгоритма

Применение метода Якоби к матрице $A = (G^TG)$ можно описать следующим образом:

Если $G = U\Sigma V^T$ и $\Sigma = diag(\sigma_{i})$, то алгоритм вычисляет сингулярные числа $\sigma_{i}$, матрицу $U$ левых сингулярных векторов и матрицу $V$ правых сингулярных векторов по следующей схеме:

repeat
    for [math]j=1[/math] to [math]n-1[/math]
        for [math]k=j+1[/math] to [math]n[/math]
            обратиться к процедуре One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
        end for
    end for
пока [math]G^TG[/math] не станет достаточно близка к диагональной матрице
Положить [math]\sigma_{i} = ||G(:,i)||_2 [/math] (норма [math]i[/math]-го столбца в [math]G[/math])
Положить [math]U = [u_{1},\dots, u_{n}][/math], где [math]u_{i} = G(:,i)/\sigma_{i}[/math]
Положить [math]V = J[/math], где [math]J[/math] - накопленное произведение вращений Якоби.

Где процедура One-Sided-Jacobi-Rotation является метод односторонних вращений Якоби:

proc One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
    вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]
         \begin{align}
         \tau &= {a_{jj} - a_{kk}}/{2a_{jk}} \\
         t &= {sign(\tau)}/(|\tau| + \sqrt{1 + \tau^2}) \\
         c &= 1/(\sqrt{1 + t^2}) \\
         s &= ct \\
         G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}[/math]
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

1.6 Последовательная сложность алгоритма

Для одного вращения Якоби необходимо выполнить $O(n)$ операций умножения и сложения.

Всего вариантов выбора $j$ и $k$ существует $\frac{n(n-1)}{2}$.

Таким образом последовательный алгоритм Якоби вычисления сингулярных чисел и векторов является алгоритмом с кубической сложностью.

1.7 Информационный граф

Граф алгоритма состоит из четырех групп вершин

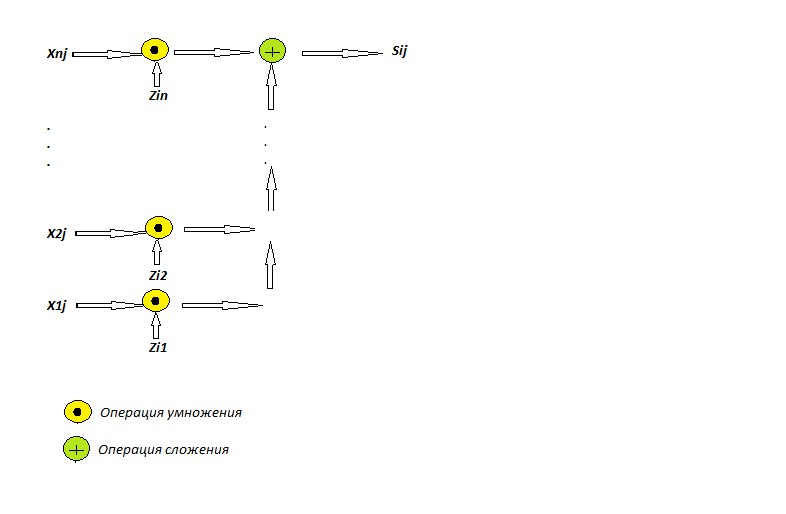
(А)Первая группа вершин расположена в двумерной области, соответствующая ей операция - вычисление элементов $a_{jj},a_{jk},a_{kk}$ матрицы произведения $A = (G^TG)$. Где $j$ изменяется от $1$ до $n-1$, принимая все целочисленные значения, $k$ изменяется от $j+1$ до $n$, принимая все целочисленные значения.

Граф вычисления каждого из элементов приведен на рисунке 1, где значениям $g_{ij}$ соответствуют обозначения $x_{ij}$, а элементам $g^T_{ij}$ обозначения $z_{ij}$. Значение $s_{ij}$ является значением результирующего элемента.

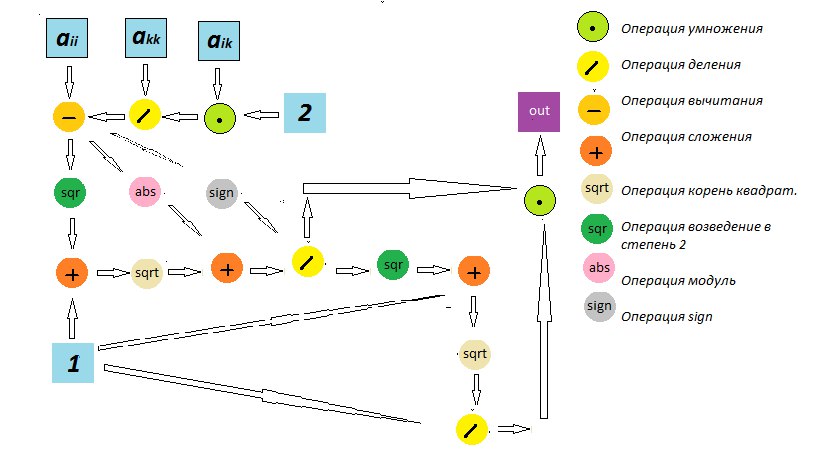
(Б)Вторая группа вершин расположена в двумерной области, соответствующая ей операция – вычисление $c$ и $s$.

Информационный граф с входными и выходными данными вычисления пункта (Б) представлен на рисунке 2.

(В)Третья группа вершин расположена в двумерной области, соответствующая ей операция вычисление значений элементов $g_{jm}^{(i+1)} = g_{mj}^{(i+1)}$ и $g_{km}^{(i+1)} = g_{mk}^{(i+1)}$, $m \ne j,k$.

(Г)Четвертая группа вершин расположена в двумерной области, соответствующая ей операция вычисление значений элементов $g_{jj}^{(i+1)}$ и $g_{kk}^{(i+1)}$.

Элементы групп (В) и (Г) вычисляются аналогично вычислению элементов матрицы произведения, т.к. фактически представляют собой перемножение матриц $G$ и $R$

Рисунок 1. Информационный граф с входными и выходными параметрами вычисления каждого элемента матрицы произведения.

Рисунок 2. Информационный граф с входными и выходными параметрами вычисления значений $c$ и $s$.

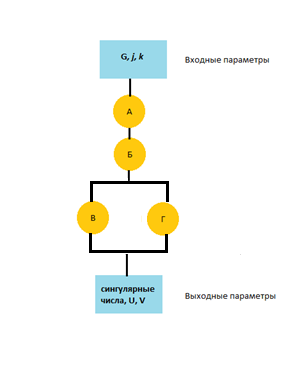
Обобщенный граф метода Якоби представлен на рисунке 3, где буквами А, Б, В и Г обозначено вычисление групп вершин (А), (Б), (В) и (Г).

Рисунок 3. Обобщенный граф алгоритма вычисления сингулярных чисел и векторов методом Якоби.

1.8 Ресурс параллелизма алгоритма

Для выполнения одной итерации метода Якоби требуется последовательно выполнить несколько ярусов:

1. вычислить $\tau$
2. вычислить $t$
3. вычислить $c$
4. выполнить поворот матрицы $G$ с параллельным выполнением $2(n-2)$ операций вычисления элементов матрицы $g_{jm}^{(i+1)} = g_{mj}^{(i+1)}$ и $g_{km}^{(i+1)} = g_{mk}^{(i+1)}$, $m \ne j,k$, а также вычисления элементов $g_{jj}^{(i+1)}$ и $g_{kk}^{(i+1)}$.

Суммарное количество итераций равно $\frac{n(n-1)}{2}$ (Различные варианты выбора $j$ и $k$).

Асимптотически метод сходится квадратично.

Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью $O(n^2)$ , а при классификации по ширине ЯПФ — к алгоритмам со сложностью $O(n)$.

1.9 Входные и выходные данные алгоритма

Входные данные: плотная матрица $G$ размера $n$х$n$, где $A= G^TG$ – симметрическая матрица.

Объём входных данных: $n^2$ (т.к. для хранения матрицы $G$ используем двумерный массив размера $n$х$n$)

Выходные данные: $\sigma_{i}$ - сингулярные числа, матрица $U$ левых сингулярных векторов и матрица $V$ правых сингулярных векторов.

Объём выходных данных: $2n^2 + n$ (т.к. необходимо хранить вектор сингулярных чисел длины $n$, а также две матрицы $U, V$ левых и правых сингулярных векторов размера $n$х$n$).

1.10 Свойства алгоритма

Метод Якоби является самым медленным из имеющихся алгоритмов вычисления сингулярных чисел и сингулярных векторов матрицы. Тем не менее, для матриц $G$, которые могут быть представлены в виде $G=DX$, где $D$ - диагональная, а $X$ - хорошо обусловлена, он способен вычислять сингулярные числа и вектора намного точнее, чем другие методы.

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных является линейной.

Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности (число итераций зависит от входных данных и порогового значения).

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Метод Якоби нахождения сингулярных значений и векторов реализован в таких пакетах, как LAPACK, LINPACK/EISPACK, Intel MKL .

Так же функция Якоби реализована в пакете Matlab.

Т. к. алгоритм считается медленным, он не включен во многие известные пакеты.

3 Литература

1. Дж. Деммель Вычислительная линейная алгебра. Изд. Мир, 2001.