Участник:Ivan kolosov/Алгоритм кластеризации, основанный на сетях Кохоннена

Основные авторы описания: И.Ю.Колосов.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задача кластеризации — это задача, в которой требуется разбить объекты во входных данных на группы, иначе называемые кластерами, таким образом, что внутри каждого кластера объекты в каком-то смысле похожи, а объекты в разных кластерах в каком-то смысле различны. Для этой задачи финским ученым Теуво Кохоненом в 80-е годы был разработан алгоритм кластеризации, основанный на использовании нейронной сети.

Алгоритм кластеризации, основанный на сетях Кохонена, предназначен для кластеризации вещественных векторов. В основе алгоритма лежит однослойная нейронная сеть, называемая картой Кохонена. Нейроны образуют сетку, в которой каждый нейрон имеет свои координаты. У каждого нейрона есть вектор весов, размерность которого равна размерности входных векторов. Все узлы входного слоя соединены с каждым из нейронов. Всюду в данной статье будем считать, что сетка нейронов двумерная, хотя ее размерность может выбираться произвольно, в том числе она может быть одномерной или трехмерной

Для того, чтобы определить кластер, к которому принадлежит данный входной вектор, вектор подают во входной слой сети. Для каждого нейрона вычисляется расстояние между входным вектором и вектором весов. Нейрон с наименьшим расстоянием между вектором весов и входным вектором активируется, обозначая принадлежность входного вектора соответствующему кластеру. Таким образом, число кластеров определяется числом нейронов. Особенностью работы алгоритма является то, что близкие друг к другу входные векторы активируют нейроны, близкие друг к другу на сетке. Это свойство оказывается удобным для визуализации кластеризованных данных.

Процесс обучения сети состоит в «соревновании» между нейронами. На каждом шаге случайным образом выбирается один из входных векторов. Из всех нейронов выбирается нейрон-победитель, который имеет наименьшее расстояние между вектором весов и входным вектором. Векторы весов всех нейронов, находящихся в пределах радиуса обучения от нейрона-победителя, сдвигаются в сторону входного вектора Вектор весов этого нейрона сдвигается в сторону входного вектора. Также в сторону входного вектора сдвигаются векторы весов остальных нейронов, причем степень сдвига зависит от расстояния до нейрона-победителя на сетке. В результате этого процесса векторы весов нейронов распределяются по пространству входных векторов.

1.2 Математическое описание алгоритма

Ниже описаны используемые обозначения, а также формулы, по которым производится счет алгоритма. Далее приведены шаги алгоритма обучения сети и шаги алгоритма использования сети.

1.2.1 Обозначения и формулы

Входные данные: набор вещественных векторов [math]x_1, x_2, ..., x_N, x_i \in R^m[/math], [math]N[/math] — число входных векторов

Текущее время: [math]t[/math]

Входной вектор, выбранный случайным образом в момент времени [math]t[/math]: [math]x^{t}[/math]

Число нейронов: [math]n[/math]

Размерность сетки нейронов: [math]D[/math]. Как упоминалось выше, всюду в данной статье считаем сетку двумерной, т.е. [math]D = 2[/math]

Размер двумерной сетки нейронов: [math]k[/math]

Веса нейронов: набор векторов [math]w_{1}^{t}, w_{2}^{t}, ..., w_{n}^{t}[/math], где [math]w_{j}^{t}[/math] принадлежит [math]R^m[/math], [math]n[/math] — число нейронов, [math]t[/math] — текущее время

Нейрон-победитель: его номер определяется формулой [math]c = arg \min_{j} \parallel x^{t} - w_{j}^{t} \parallel[/math]

Функция скорости обучения сети: [math]a\left(t\right) = a_0 \cdot exp\left\{-\frac{t}{\lambda_{1}}\right\}[/math], где [math]a_0, \lambda_{1}[/math] — настраиваемые параметры. Возможно использование других функций.

Радиус нейрона-победителя: [math]\sigma\left(t\right) = \sigma_0 \cdot exp\left\{-\frac{t}{\lambda_{2}}\right\}[/math], где [math]\sigma_0, \lambda_{2}[/math] — настраиваемые параметры.

Функция расстояния между нейроном-победителем и другим нейроном: [math]h\left(d_{cj}, t\right) = exp\left\{-\frac{d_{cj}^2}{2 \cdot \sigma^2\left(t\right)}\right\}[/math], где [math]d_{cj}[/math] — расстояние между нейроном-победителем и другим нейроном на сетке.

Функция соседства нейрона [math]j[/math]: [math]h_{j}\left(t\right) = h\left(d_{cj}, t\right) \cdot a\left(t\right)[/math], где [math]h\left(d_{cj}, t\right)[/math] — функция расстояния между нейроном [math]j[/math] и нейроном-победителем.

Данные, вычисляемые при обучении сети: веса нейронов в момент времени [math]t + 1[/math], вычисляемые по формуле [math]w_{j}^{t + 1} = w_{j}^{t} + h_j(t) \cdot \left[x^{t} - w_{j}^{t}\right][/math], где [math]x^{t}[/math] — случайным образом выбранный входной вектор, [math]w_{j}^{t}[/math] — вектор весов нейрона [math]j[/math] в момент времени [math]t[/math], [math]h_{j}\left(t\right)[/math] — функция соседства нейрона [math]j[/math]

Данные, вычисляемые при использовании сети: номер нейрона-победителя [math]c[/math]

1.2.2 Шаги обучения сети

1. Проинициализировать время: [math]t = 0[/math] и выбрать максимальное время [math]t_{max}[/math]
2. Проинициализировать векторы весов нейронов случайным образом
3. Случайным образом выбрать входной вектор [math]x^{t}[/math]
4. Вычислить расстояния от векторов весов нейронов до входного вектора
5. Найти номер [math]c[/math] нейрона-победителя, у которого расстояние от вектора весов до входного вектора минимально
6. Вычислить радиус обучения [math]\sigma\left(t\right)[/math]
7. Вычислить расстояния на сетке от нейрона-победителя до остальных нейронов
8. Для всех нейронов, находящихся в пределах радиуса обучения от нейрона-победителя, вычислить новые векторы весов
9. Увеличить время: [math]t = t + 1[/math]
10. Если текущее время [math]t[/math] равно максимальному [math]t_{max}[/math], то алгоритм завершается. Иначе перейти на шаг 3.

1.2.3 Шаги использования сети

1. Вычислить расстояния от векторов весов нейронов до входного вектора
2. Активировать нейрон с минимальным расстоянием

1.3 Вычислительное ядро алгоритма

Алгоритм имеет два вычислительных ядра — нахождение нейрона-победителя и пересчет векторов весов нейронов. Вычисление этих ядер повторяется друг за другом при обучении сети. При использовании сети выполняется только нахождение нейрона-победителя, при этом нейрон-победитель активируется и обозначает кластер, к которому принадлежит входной вектор.

Для нахождения нейрона-победителя вычисляются расстояния между векторами весов нейронов и входным вектором. Нейрон с минимальным расстоянием выбирается в качестве нейрона-победителя.

Для пересчета векторов весов нейронов вычисляется текущий радиус обучения, затем вычисляются расстояния на сетке между нейроном-победителем и остальными нейронами. Векторы весов нейронов, вошедших в радиус обучения, пересчитываются в соответствии с формулами.

1.4 Макроструктура алгоритма

Можно выделить следующие макрооперации:

1. Выбор входного вектора
2. Вычисление расстояний между векторами весов нейронов и входным вектором
3. Нахождение минимального расстояния
4. Нахождение радиуса обучения
5. Нахождение текущей скорости обучения
6. Вычисление расстояний между нейронами на сетке
7. Пересчет векторов весов

1.5 Схема реализации последовательного алгоритма

1.5.1 Последовательность выполнения обучения сети

1. Выбрать параметры [math]a_0, \lambda_{1}, \sigma_0, \lambda_{2}, t_{max}[/math]
2. [math]t = 0[/math]

До тех пор, пока [math]t \neq t_{max}[/math], выполняются следующие шаги:

1. Случайным образом выбрать входной вектор [math]x^{t}[/math]
2. [math]\forall j \in \left\{0, \ldots, n\right\}[/math] вычислить [math]d_{j}^{t} = \parallel x^{t} - w_{j}^{t} \parallel[/math] — расстояние между вектором весов нейрона [math]j[/math] и входным вектором
3. Найти [math]c = arg \min_{j} d_{j}^{t}[/math]
4. Вычислить текущий радиус обучения [math]\sigma\left(t\right) = \sigma_0 \cdot exp\left\{-\frac{t}{\lambda_{2}}\right\}[/math]
5. Вычислить текущую скорость обучения [math]a\left(t\right) = a_0 \cdot exp\left\{-\frac{t}{\lambda_{1}}\right\}[/math]
6. [math]\forall j \in \left\{0, \ldots, n\right\} \setminus \left\{c\right\}[/math] вычислить расстояние от нейрона [math]j[/math] до нейрона-победителя: [math]d_{cj}[/math].
7. [math]\forall j: d_{c,j} \lt \sigma\left(t\right)[/math] посчитать новый вес нейрона [math]j[/math]: [math]w_{j}^{t + 1} = w_{j}^{t} + exp\left\{-\frac{d_{cj}^2}{2 \cdot \sigma^2\left(t\right)}\right\} \cdot a\left(t\right) \cdot \left[x^{t} - w_{j}^{t}\right][/math]
8. [math]t = t + 1[/math]

1.5.2 Последовательность выполнения использования сети

1. [math]\forall j \in \left\{0, \ldots, n\right\}[/math] вычислить [math]d_{j} = \parallel x - w_{j} \parallel[/math] — расстояние между вектором весов нейрона [math]j[/math] и входным вектором
2. Найти [math]c = arg \min_{j} d_{j}[/math]
3. Активировать нейрон [math]c[/math]

1.6 Последовательная сложность алгоритма

1.6.1 Алгоритм обучения сети

1.6.1.1 В терминах макроопераций

Число операций выбора входного вектора: [math]t_{max}[/math]

Число операций вычисления расстояний между векторами весов нейронов и входным вектором: [math]t_{max} \cdot n[/math]

Число операций нахождения минимального расстояния: [math]t_{max}[/math]

Число операций нахождения радиуса обучения: [math]t_{max}[/math]

Число операций нахождения текущей скорости обучения: [math]t_{max}[/math]

Число операций вычисления расстояний между нейронами на сетке: [math]t_{max} \cdot (n - 1)[/math]

Число операций пересчета векторов весов нейронов: [math]t_{max} \cdot n[/math]

1.6.1.2 В терминах низкоуровневых операций

Число сложений и вычитаний: [math]t_{max} \cdot \left(n \cdot \left(4m - 1\right) + \left(n - 1\right) \cdot \left(2D - 1\right)\right)[/math]

Число умножений: [math]t_{max} \cdot \left( n \cdot \left(2m + 4\right) + \left(n - 1\right) \cdot D + 2\right)[/math]

Число делений: [math]t_{max} \cdot \left(n + 2\right)[/math]

Число вычислений квадратного корня: [math]t_{max} \cdot \left(2n -1\right)[/math]

Число вычислений экспоненты: [math]t_{max} \cdot \left(n + 2\right)[/math]

1.6.2 Алгоритм использования сети

1.6.2.1 В терминах макроопераций

Число операций вычисления расстояний между векторами весов нейронов и входным вектором: [math]n[/math]

Число операций нахождения минимального расстояния: [math]1[/math]

1.6.2.2 В терминах низкоуровневых операций

Число умножений: [math]n \cdot m[/math]

Число сложений и вычитаний: [math]n \cdot (2m - 1)[/math]

Число вычислений квадратного корня: [math]n[/math]

1.7 Информационный граф

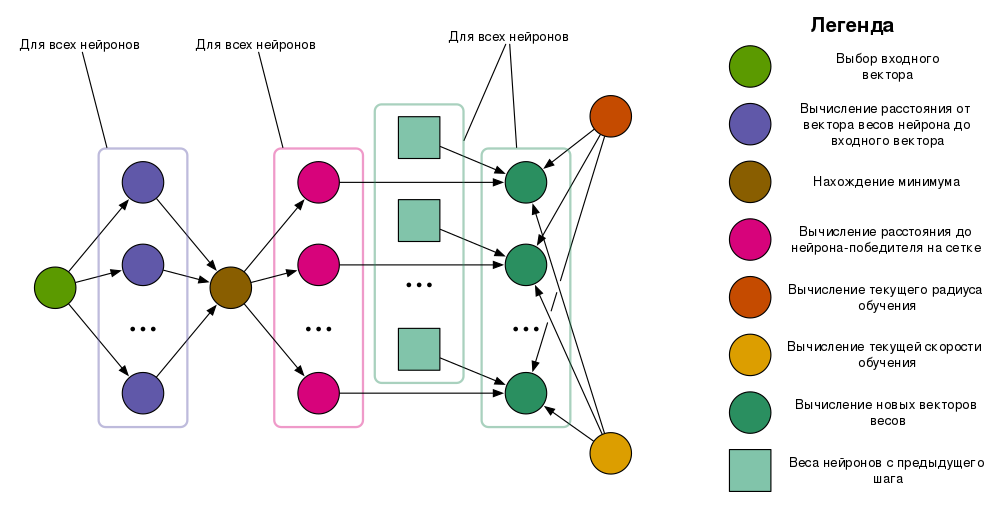
Опишем вершины, входящие в информационный граф, соответствующие им операции, а также входные и выходные данные.

Выбор входного вектора — вершинам данного типа соответствует операция выбора входного вектора. Входные данные отсутствуют, выходом является случайным образом выбранный входной вектор.

Вычисление расстояния от вектора весов нейрона до входного вектора — входными данными операции являются вектор весов нейрона и входной вектор. Выходом операции является евклидово расстояние между вектором весов и входным вектором.

Нахождение минимума — на входе операции набор расстояний, на выходе — номер наименьшего расстояния

Вычисление расстояния до нейрона-победителя на сетке — на входе номер нейрона-победителя и номер нейрона, на выходе — расстояние на сетке между нейроном-победителем и нейроном

Вычисление текущего радиуса обучения — на входе текущее время и заранее заданные параметры радиуса обучения, на выходе — текущий радиус обучения

Вычисление текущей скорости обучения — на входе текущее время и заранее заданные параметры скорости обучения, на выходе — текущая скорость обучения.

Вычисление новых векторов весов — на входе расстояние на сетке между нейроном и нейроном-победителем, вектор весов нейрона, текущий радиус обучения и текущая скорость обучения. На выходе операции новый вектор весов нейрона. Новый вектор весов может совпадать со старым, например, в случае, когда нейрон не входит в радиус обучения нейрона-победителя.

Активация нейрона-победителя — на входе номер нейрона.

Для ясности наличие некоторых параметров у операций не отражено на изображении информационного графа.

Рисунок 1. Граф алгоритма обучения сети Кохонена. Изображена одна итерация алгоритма обучения сети Кохонена, происходящая при фиксированном значении времени. Две следующие друг за другом итерации связаны через векторы весов нейронов, которые пересчитываются на каждом итерации и используются на следующей итерации для подсчета расстояний между векторами весов нейронов и входным вектором и для пересчета весов. Для ясности на изображении не показано, что веса нейронов используются при подчете расстояний.

Рисунок 2. Граф алгоритма использования сети Кохонена

1.8 Ресурс параллелизма алгоритма

1.8.1 Алгоритм обучения сети

Для обучения сети требуется [math]t_{max}[/math] раз последовательно выполнить следующие ярусы:

• Выбор входного вектора (ширина 1)
• Вычисление расстояний от векторов весов нейронов до входного вектора (ширина [math]n[/math])
• Нахождение минимума (ширина 1)
• Вычисление расстояния до нейрона-победителя на сетке (ширина [math]n[/math])
• Вычисление новых векторов весов (ширина [math]n[/math])

Операции вычисления текущего радиуса обучения и текущей скорости обучения могут как представлять собой два отдельных радиуса шириной 1, так и входить в ярус вычисления новых векторов весов.

Наличие двух ярусов шириной 1 является проблемой, так как во время вычисления этих ярусов большая часть ресурсов будет простаивать.

1.8.2 Алгоритм использования сети

Для использования сети требуется последовательно выполнить следующие ярусы:

• Вычисление расстояний от векторов весов нейронов до входного вектора (ширина [math]n[/math])
• Нахождение минимума (ширина 1)
• Активация нейрона (ширина 1)

1.9 Входные и выходные данные алгоритма

1.9.1 Алгоритм обучения сети

Входные данные: набор вещественных векторов [math]x_1, x_2, ..., x_N, x_i \in R^m[/math], [math]N[/math] — число входных векторов

Объем входных данных: [math] N \cdot m [/math]

Выходные данные: набор векторов весов нейронов [math]w_{1}, w_{2}, ..., w_{n}, w_{j} \in R^m[/math], где [math]n[/math] — число нейронов

Объем выходных данных: [math] n \cdot m [/math]

1.9.2 Алгоритм использования сети

Входные данные: Входной вектор [math]x \in R^m[/math], векторы весов нейронов [math]w_{1}, w_{2}, ..., w_{n}, w_{j} \in R^m[/math], где [math]n[/math] — число нейронов

Объем входных данных: [math] (n + 1) \cdot m [/math]

Выходные данные: номер активированного нейрона [math]c[/math]

Объем выходных данных: [math] 1 [/math]

1.10 Свойства алгоритма

Недостатком алгоритма является то, что число кластеров необходимо задавать заранее, задавая число нейронов. Кроме того, имеет значение конфигурация сетки — ее размерность и размеры.

Алгоритм не подходит для дискретных или категорических данных, кроме того, он не подходит для использования с неполными данными.

Алгоритм обучения сети является недетерминированным, так как, во-первых, на каждом шаге необходимо случайным образом выбирать входной вектор, во-вторых, результат работы зависит от инициализации векторов весов нейронов.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Существует реализация алгоритма, написанная на языке C автором алгоритма Теуво Кохоненом при поддержке других исследователей. Лицензия, под которой выпущен код, разрешает только использование в научных целях. Ссылка.

Другая реализация алгоритма написана на языке C++ и выпущена под лицензией BSD, разрещающей использование в коммерческих целях. Также эта реализация позволяет конфигурировать размеры сетки нейронов. Ссылка.

3 Литература

<references \>