Быстрое дискретное преобразование Фурье (БПФ)

Эта работа прошла предварительную проверку Дата последней правки страницы: 14.11.2016 Данная работа соответствует формальным критериям. Проверено IgorS.

Авторы: Чачба А.Н., Костоев Р.С.

Чачба А.Н. заполнил половину всех заполненных пунктов (а именно 1.1, 1.2, 1.6, 1.8, 1.9) и построил информационный граф алгоритма, Костоев Р.С. написал программу и провел серию запусков на суперкомпьютере и заполнил вторую половину пунктов. Оба после заполнения исправляли найденные ошибки во всех пунктах.

Быстрое преобразование Фурье (БПФ)
Последовательный алгоритм
Последовательная сложность	[math]O(N \log N)[/math]
Объём входных данных	[math]N[/math]
Объём выходных данных	[math]N[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(\log N)[/math]
Ширина ярусно-параллельной формы	[math]O(N)[/math]

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Преобразование Фурье - взаимно однозначное отображение одной функции вещественной, называемой таргетным сигналом, с другой функцией вещественной переменной, называемой образом Фурье или спектром исходной функции по формуле:

[math] \hat{f}(\omega)=\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^{\infty}f(x)e^{-ix\omega}\,dx [/math]

Дискретное преобразование Фурье, в свою очередь, есть аналог непрерывного преобразования Фурье, но для дискретного сигнала содержащего [math]N[/math] отсчетов. Широко применяется в цифровой обработке сигналов, теории вероятностей, криптографии и акустике. Преобразование Фурье обратимо, причем обратное преобразование имеет практически ту же форму, что и прямое. Преобразование Фурье имеет сложность [math]O(N^2)[/math], но существует быстрый вариант преобразование Фурье со сложностью [math]O(N\log{N})[/math].

1.2 Математическое описание алгоритма

Пусть исходный сигнал имеет значения [math]x_n,\quad n = 0,\dots,N-1[/math], тогда дискретное прямое преобразование Фурье (ДПФ) имеет вид:

[math] X_k = \sum_{n=0}^{N-1}x_ne^{-\frac{2\pi i}{N}kn},\quad k = 0, \dots, N-1 [/math]

Обозначим [math] \varepsilon_{N} = e^{-\frac{2\pi i}{N}}[/math], тогда ДПФ можно перезаписать в матричной форме:

[math] \bar X = A\bar x [/math]

где матрица [math]A = \{e^{-\frac{2\pi i}{N}(i - 1)(j - 1)}\}_{i,j=1}^{N}[/math]

1.3 Вычислительное ядро алгоритма

Пусть, для простоты [math] N = km[/math], тогда рекурсивная реализация преобразования Фурье, за счет [math]{k}[/math] рекурсий на первом этапе и [math]m[/math] на последнем этапе, имеет суммарную сложность [math]O(Nk + Nm + km) = O(N(k + m))[/math].

В случае, например [math]N = 2^n[/math] сложность БПФ составляет [math]O(N\log{N})[/math].

В общем же случае, когда [math]N = \prod_{i=1}^np_i[/math] сложность БПФ составляет [math] O(N(\sum_{i=1}^np_i))[/math].

1.4 Макроструктура алгоритма

Макроструктура БПФ для случая [math]N = km[/math] описывается рекурсивно:

1. [math]k[/math] независимых преобразований векторов меньшей размерности [math]m[/math]
2. Умножение элементов на поворотные коэффициенты ([math]N[/math] умножений)
3. [math]m[/math] обратных преобразований векторов размерностей [math]k[/math]

1.5 Схема реализации последовательного алгоритма

Рекурсивный метод для случая [math]N = 2^k[/math], без оптимизации на C++:

#include <vector>
#include <complex>

using namespace std;

typedef complex<double> cd;
typedef vector<cd> vcd;

vcd fft(const vcd &as) { 
  int n = as.size();
  if (n == 1) return vcd(1, as[0]);

  vcd w(n); // Calculate roots
  for (int i = 0; i < n; i++) {
    double alpha = 2 * M_PI * i / n;
    w[i] = cd(cos(alpha), sin(alpha));
  }

  vcd A(n / 2), B(n / 2);
  for (int i = 0; i < n / 2; i++) {
    A[i] = as[i * 2];
    B[i] = as[i * 2 + 1];
  }
  vcd Av = fft(A);
  vcd Bv = fft(B);
  vcd res(n);
  for (int i = 0; i < n; i++)
    res[i] =   Av[i % (n / 2)] +
        w[i] * Bv[i % (n / 2)];
  return res;
}

В последовательном варианте можно бороться за улучшение константы сложности, предподсчитав значения соответствующих коэффициентов.

1.6 Последовательная сложность алгоритма

Алгоритм состоит из трех этапов, следовательно если [math]N = \prod_{i = 1}^np_i[/math], то общая сложность составляет порядка [math]O(N\sum_{i=1}^np_i)[/math] операций.

Пусть существует некоторое фиксированное число [math]P[/math], такое что:

[math] p_i \leq P \quad \forall i = 1...n, [/math]

тогда, учитывая, что [math]n \leq \log_{P}{N}[/math], сложность алгоритма можно записать в виде [math]O(N\log{N})[/math].

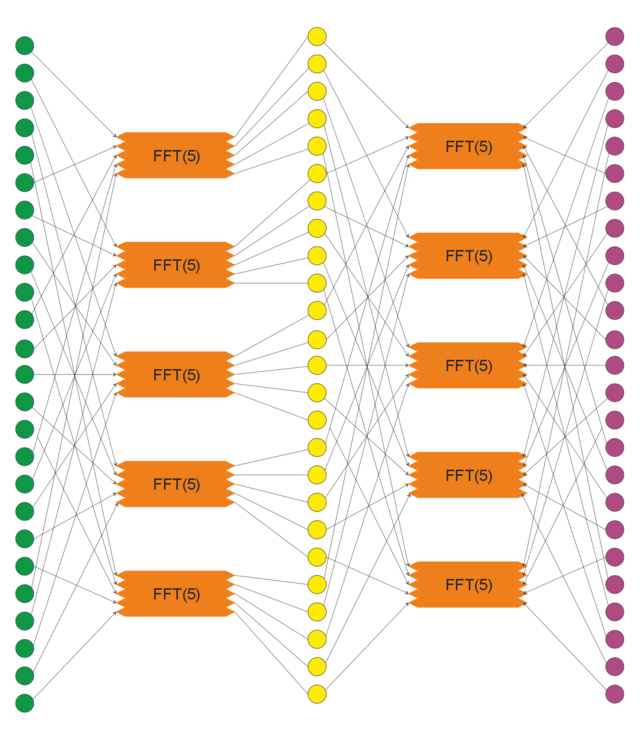
1.7 Информационный граф

Рисунок 1. Информационный граф преобразования Кули-Тьюки для [math]N = km = 25, k = 5, m = 5[/math]. Желтые вершины - умножение на поворотные множители.

1.8 Ресурс параллелизма алгоритма

В силу независимости всех рекурсивных вызовов и того факта, что путь максимальной длины в графе (так называемый критический путь) имеет порядок [math]O(\log{N})[/math], можно утверждать, что параллельная сложность алгоритма составит [math]O(\log{N})[/math].

Замечание: формально основание логарифма на каждом рекурсивном шаге зависит от множителя в факторизации [math]N[/math], потому использована О-символика.

При условии ограниченности количества доступных вычислительных узлов рекомендуется выбирать множители в разложении числа $N$ близкими к числу доступных узлов, таким образом доступные ресурсы будут использованы максимально эффективно.

Итого алгоритм относится к логарифмическому классу алгоритмов по параллельной сложности.

1.9 Входные и выходные данные алгоритма

Входные данные: Чаще всего для обработки сигналов в качестве входных данных для БПФ подается вектор размерности [math]N[/math] вещественных элементов. Но БПФ работает и для случая элементов над комплексным полем. Таким образом, например, можно экономить на количестве применений БПФ в некоторой конкретной задаче путем приведения двух векторов вещественных чисел к одному вектору комплексных чисел с вещественной частью равной первому вектору и комплексной частью равной второму вектору: [math]x, y[/math] - исходные сигналы. Обозначим [math]z = x + iy[/math], а [math]F(k, x)[/math] - это [math]k[/math]-ый коэффициент образа Фурье вектора [math]x[/math]. Тогда:

[math]F(k, x) = \frac{F(k, z) + F(k, \bar z)}{2}[/math]

[math]F(k, y) = -i\frac{F(k, z) - F(k, \bar z)}{2}[/math]

Учитывая, что [math]F(k, \bar z) = \overline{F(N - k, z)}[/math], получаем:

[math]F(k, x) = \frac{F(k, z) + \overline{F(N-k, z)}}{2}[/math]

[math]F(k, y) = -i\frac{F(k, z) - \overline{F(N-k,z)}}{2}[/math]

Такой способ позволяет приблизительно в два раза уменьшить количество вычислений.

Выходные данные: Вектор размерности [math]N[/math] комплексных чисел - спектр исходного сигнала.

1.10 Свойства алгоритма

Матрица Вандермонда преобразования [math]A = \{e^{-\frac{2\pi i}{N}(i - 1)(j - 1)}\}_{i,j=1}^{N}[/math] такая, что:

[math] A^{-1} = \frac{1}{N}A^* [/math]

Таким образом обратное преобразование Фурье с точностью до нормирующего множителя и сопряжения элементов матрицы совпадает с прямым.

2 ЧАСТЬ. Программная реализация алгоритма

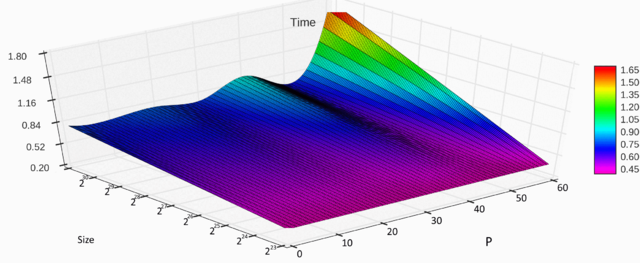
2.4 Масштабируемость алгоритма и его реализации

Рисунок 2. Время выполнения параллельной реализации БПФ в секундах. Size - число элементов массива. Р - число использованных процессоров.

Рисунок 3. Эффективность параллельной реализации БПФ. Size - число элементов массива. Р - число использованных процессоров. Эффективность в пределах от 0 до 1.

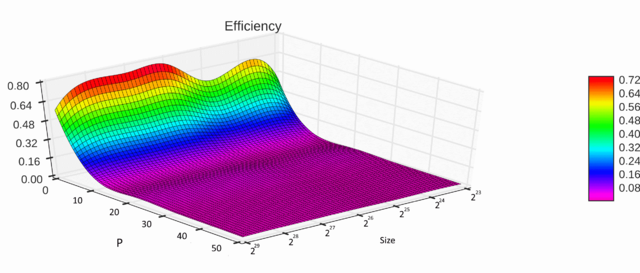
Как видно из графика, эффективность параллельной реализации резко падает с ростом количества используемых процессоров, связано это с увеличением количества накладных расходов.

2.7 Существующие реализации алгоритма

• Самая популярная библиотека для работы с преобразованиями Фурье это FFTW
• Реализация от Intel в рамках Math Kernel Library
• Реализация ДПФ на графических картах от NVidia - cuFFT

3 Литература

• Бахвалов Н. С., Жидков Н. П., Кобельков. Г. М. — 6-е изд. — М. : БИНОМ. Лаборатория знаний, 2008. — 636 с.
• Описание алгоритма на Вкипедии: Быстрое преобразование Фурье
• Материалы лекций по "Алгоритмам и структурам данных" Школы Анализа Данных Яндекса