Участник:Victoria Stepanischeva/Быстрое преобразование Фурье (FFT)

Авторы:

• Степанищева В.С., группа 601 (Общее описание алгоритма, Вычислителное ядро алгоритма, Макроструктура алгоритма, Информационный граф, Ресурс параллелизма алгоритма)
• Мунькин И.А., группа 601 (Математическое описание алгоритма, Схема реализации последовательного алгоритма, Последовательная сложность алгоритма, Входные и выходные данные алгоритма, Свойства алгоритма, Существующие реализации алгоритма)

Быстрое преобразования Фурье
Последовательный алгоритм
Последовательная сложность	[math]O(N \; log \, N)[/math]
Объём входных данных	[math]N[/math]
Объём выходных данных	[math]N[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(log \,N)[/math]
Ширина ярусно-параллельной формы	[math]N[/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм быстрого преобразования Фурье, включая его рекурсивную реализацию, был использован Карлом Фридрихом Гауссом еще в 1805 году для интерполяции траекторий астероидов, однако эта работа не получила широкого признания. Алгоритм быстрого преобразования Фурье обрел свою популярность благодаря работе James Cooley, работающего в то время в IBM, и John Tukey, параллельно принимающего участие в разработках Bell Labs и работающего в Принстонском университетe. В их статье, изданной в 1965 году, они представили подробное описание алгоритма и его программной реализации.

1.1.1 Разновидности алгоритма быстрого преобразования Фурье

Помимо традиционного и наиболее распространенного алгоритма Cooley-Tukey существует также несколько других часто используемых реализаций алгоритма быстрого преобразования Фурье.

1.1.1.1 PFA-алгоритм

Алгоритм prime-factor (PFA), также называемый алгоритмом Good-Thomas, представляет собой алгоритм быстрого преобразования Фурье, который представляет дискретное преобразование Фурье размера [math]N = N_1 \cdot N_2[/math] в виде двумерного [math]N_1 \times N_2[/math] дискретного преобразования Фурье, при условии, что [math]N_1[/math] и [math]N_2[/math] - взаимно простые числа. Представленные преобразования меньшего размера могут быть вычислены либо рекурсивным применением PFA либо используя какой-либо иной метод быстрого преобразования Фурье.

1.1.1.2 Алгоритм Bluestein

Алгоритм Bluestein, обычно называемый [math]\mathcal{Z}[/math]-чирп алгоритмом, представляет собой алгоритм быстрого преобразования Фурье, который вычисляет дискретное преобразование Фурье различных размеров с помощью представления оного в виде линейной свертки. Другой алгоритм быстрого преобразования Фурье, использующий свойства простых чисел, алгоритм Rader, также вычисляет дискретное преобразование Фурье в виде свертки.

1.1.2 Приложения быстрого преобразования Фурье

Алгоритм быстрого преобразования Фурье имеет множество областей приложения, таких как:

• Обработка изображений
• Цифровое сжатие
• Численное интегрирование
• Быстрые методы решения уравнения Пуассона
• Спектральные методы решения обыкновенных дифференциальных уравнений

Рассмотрим подробнее те приложения, с которыми мы наиболее часто сталкиваемся в повседневной жизни.

1.1.2.1 Обработка изображений

Все фильтры делят на две группы: пространственные и частотные. Типов пространственных фильтров достаточно много: линейные, медианные, изотропные и др. Процесс фильтрации в этих фильтрах основан на простом применении маски фильтра ко всем точкам изображения. В каждой точке отклик фильтра вычисляется с использованием предварительно заданных связей. Все пространственные фильтры имеют линейную трудоемкость.

Частотная фильтрация является более общим механизмом фильтрации, чем пространственная. Все пространственные фильтры можно реализовать с помощью частотных. Частотные фильтры выполняют фильтрацию изображений в частотной области. Для этого с помощью преобразования Фурье происходит получение спектра изображения. После применения фильтра к спектру изображения выполняется обратное преобразование Фурье и получается отфильтрованное изображение.

Простота фильтрации в частотной области заключается в простой интерпретации частот:

• низкие частоты - плавное изменение яркости изображения
• высокие частоты - быстрое изменение яркости изображения (границы объектов)

За счет изменения значений определенных частот можно добиться размытия изображения, повышение резкости и др.

1.1.2.2 Цифровое сжатие

Одним из первых форматов файла-контейнера для хранения записи оцифрованного аудипотока является формат WAV. Этот формат чаще всего используется в качестве оболочки для несжатого звука. При таком кодировании в WAV-файле хранится полная информация об исходном звуке, оцифрованном и проквантованном с некоторой частотой, например 44 кГц. Этой информации абсолютно достаточно для воспроизведения всех частот исходного сигнала, меньших половины частоты квантования (по теореме Котельникова ). При этом одна минута записи занимает около 15 Мб, поэтому в настоящее время очень популярным стал формат кодирования MPEG Layer-3 со сжатием.

При сжатии кодеком MPEG Layer-3 исходный звуковой сигнал разбивается на фрагменты, длительностью по 50 миллисекунд, каждый из которых анализируется отдельно. При анализе фрагмент раскладывается на гармоники по методу Фурье, из которых в соответствии с теорией восприятия звука человеческим ухом выбрасываются те гармоники, которые человек хуже воспринимает на фоне остальных:

• более тихие гармоники на фоне более громких
• звуки, замаскированные вследствие инертности слуха (так, например, если за очень громким хлопком, с задержкой в долю секунды, пойдет какой-то иной кратковременный сигнал, то его слышно не будет)

При воспроизведении файла закодированного MPEG Layer-3 производится обратное преобразование, при котором оставшиеся гармоники вновь преобразуются в звуковую волну. Поскольку часть информации об исходном сигнале была удалена, звук получается не совпадающий с исходным. Одной из основных характеристик качества аудио потока является битрейт.

Битрейт - это объем информации на каждую секунду записи:

• чем он меньше, тем меньший размер имеют файлы с одинаковой по времени длине
• чем он меньше, тем большее количество "лишних" гармоник приходится удалять

1.2 Математическое описание алгоритма

Пусть задан вектор действительных чисел [math]\left(f_1, f_2, f_3, \dots, f_{N-1} \right)[/math]

Дискретное преобразование Фурье определено следующим образом

[math] F_k = \sum_{n = 0}^{N - 1}\, f_n\, e^{\left(\frac{i2\pi kn}{N}\right)} [/math]

Обозначим [math]W_N = e^{\left(\frac{i2\pi}{N}\right)}[/math] - [math]N[/math]-ый корень единицы. Таким образом [math](W_N)^N = 1[/math]. Несложные математические преобразования приводят формулу дискретного преобразования Фурье к следующему виду

[math] F_k = \sum_{n = 0}^{N - 1}\, f_n\, W_n^{-nk} [/math]

Таким образом, алгоритм вычисления дискретного преобразования Фурье состоит из 2 шагов:

1. Вычисление поворотных коэффициентов [math]W_n^{-nk},\; n,k = 0, 1, \dots, N-1[/math]
2. Вычисление коэффициентов Фурье [math]F_k,\; k = 0, 1, \dots, N-1[/math]

В основе концепции быстрого преобразования Фурье лежит идея отдельного расчета четных и нечетных коэффициентов с использованием векторов меньшего размера. Разобъем дискретное преобразование Фурье следующим образом

[math] F_k = \sum_{n = 0}^{N - 1}\, f_n\, W_{N}^{-nk} = \sum_{n = 0}^{N/2 - 1}\, g_n\, W_{N/2}^{-nk} + \sum_{n = 0}^{N/2 - 1}\, h_n\, W_{N/2}^{-nk} [/math]

Следовательно, четные и нечетные коэффициенты Фурье могут быть записаны в следующем виде:

[math] F_{2k} = \sum_{n = 0}^{N/2 - 1}\, \underbrace{ \left(f_n + f_{n + N/2}\right) }_{g_n} \, W_{N/2}^{-nk} [/math]

[math] F_{2k+1} = \sum_{n = 0}^{N/2 - 1}\, \underbrace{ \left((f_n + f_{n + N/2}) W^{-n}\right) }_{h_n} \, W_{N/2}^{-nk} [/math]

Таким образом, вычисление дискретного преобразования Фурье от [math]N[/math] коэффициентов сводится к вычислению 2 дискретных преобразований Фурье от [math]N/2[/math] коэффициентов. Применяя данную идею рекурсивно, получаем алгоритм быстрого преобразования Фурье.

1.3 Вычислительное ядро алгоритма

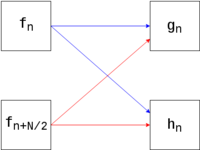
В случае размера входных данных равному [math]N = 2^M[/math] вычислительным ядром алгоритма являются так называемые "бабочки". В элементарном случае "бабочка" является двухточечным преобразованием.

[math] g_n = f_n + f_{n + N/2} [/math]

[math] h_n = \left(f_n - f_{n + N/2}\right)\, W^{-n} [/math]

1.4 Макроструктура алгоритма

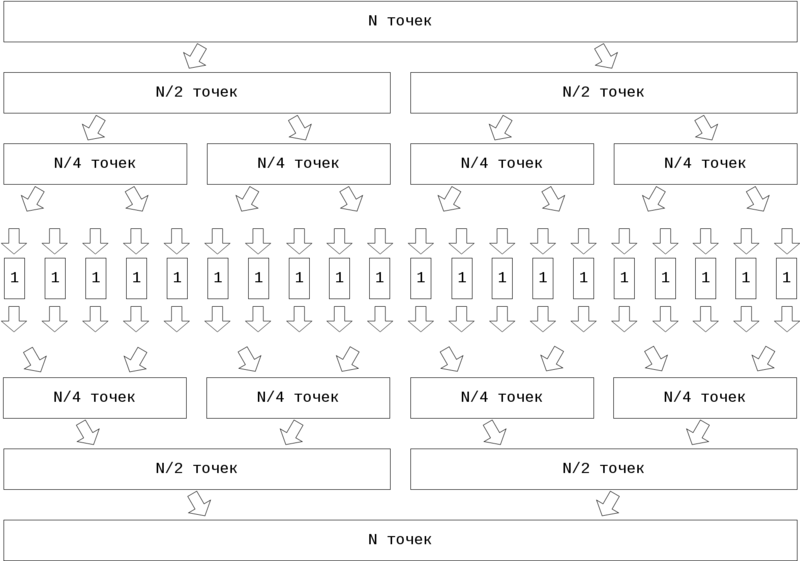
Описываемый алгоритм работает по принципу "разделяй и властвуй".

Рассмотрим общую структуру для входных данных размера [math]N = N1 \cdot N2[/math]

1. Исходное множество точек разбивается на [math]N2[/math] равных подмножеств размером [math]N1[/math].
2. Над каждым из полученных множеств выполняется быстрое преобразование Фурье. Для его вычисления над каждым из подмножеств рассматриваемого множества снова выполняется деление на равные части. Такое разбиение продолжается до тех пор, пока количество элементов, над которыми необходимо выполнить быстрое преобразование Фурье, не будет равно одному.
3. После этого выполняется объединение всех промежуточных результатов. Полученные на предыдущем шаге множества объединяются за линейное время.

Ниже представлена схема алгоритма Cooley-Tukey для [math]N = 2^M[/math]

1.5 Схема реализации последовательного алгоритма

Ниже представлен прототип реализации для [math]N = 2^M[/math].

use Math::Complex;

sub fft {
    my $input = shift;
    return $input if @{ $input } == 1;
    my @w = map {
        my $theta = 2 * pi * $_ / @{ $input };
        Math::Complex->make(cos($theta), sin($theta));
    } (0 .. $#input);
    my $odd  = fft([ map { $input->[2 * $_ + 1] }, (0 .. @{ $input } / 2 - 1) ]);
    my $even = fft([ map { $input->[2 * $_] }, (0 .. @{ $input } / 2 - 1) ]);
    return [ map {
        $even->[$_ % @{ $even }] + $w[$_] * $odd->[$_ % @{ $odd }];
    } (0 .. $#input) ];
};

1.6 Последовательная сложность алгоритма

Если считать только главные члены выражений для последовательной сложности алгоритма, то простой алгоритм Cooley-Tukey может быть выполнен за [math]N\, log\, N[/math] операций. Таким образом, простой алгоритм Cooley-Tukey относится к линейно-логарифмическому классу по последовательной сложности.

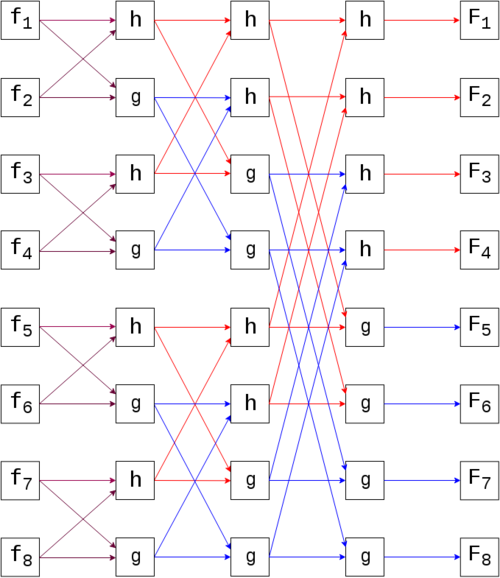
1.7 Информационный граф

Ниже представлен информационный граф для простого алгоритма Cooley-Tukey для [math]N = 8[/math], [math]\;h[/math] - операция сложения двух комплексных чисел, [math]g[/math] - операция вычитания двух комплексных чисел и умножения результата вычитания на комплексное число (поворотный множитель). В последнем столбце операций умножения не производится.

1.8 Ресурс параллелизма алгоритма

Простой алгоритм Cooley-Tukey имеет критический путь, состоящий из [math]log\, N[/math] операций сложения и вычитания и [math]log\, N[/math] операций комплексного умножения (основание логарифма зависит от выбранного на каждом шаге алгоритма разбиения). Следовательно, простой алгоритм быстрого преобразования Фурье в общем случае может быть отнесен к логарифмическому классу по параллельной сложности.

1.9 Входные и выходные данные алгоритма

Входные данные: измеренные значения сигнала в дискретных временных точках с номерами [math]0 \dots N[/math]: [math]f \in \mathbb{R}^N[/math].

Объём входных данных: [math]N[/math] .

Выходные данные: вектор компонент спектра исходного сигнала: [math]F \in \mathbb{C}^N[/math].

Объём выходных данных: [math]N[/math].

1.10 Свойства алгоритма

Обработку подмножеств, получаемых после разбиения, можно выполнять независимо, этот факт можно использовать при распараллеливании алгоритма. Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейным. Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, является логарифмической.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Наиболее популярной библиотекой, содержащей реализацию быстрого преобразования Фурье, является FFTW, изначально разработанная сотрудниками MIT Matteo Frigo и Steven G. Johnson. На сегодняшний день исходный код библиотеки распространяется под свободной лицензией GNU General Public Licence v2 с помощью сервиса Github, тем самым давая возможность сообществу принимать участие в разработке. Несмотря на то, что сама библиотека написана на языке C существуют интерфейсы для работы с ней используя такие языки программирования как Fortran, C++ и другиe.

Для разбиения преобразований, размеры которых являются составным числом, на меньшие используется одна из многочисленных реализаций алгоритма Cooley-Tukey (в зависимости от разложения на простые множители и паттернов доступа к памяти). В свою очередь для преобразований, размеры которых являются простыми числом используется либо алгоритм Raider, либо алгоритм Bluestein. Библиотека признана самой быстрой реализацией быстрого преобразования Фурье, гарантируя на любых объемах входных данных сложность [math]O \left(n\; log\, n \right)[/math]. Существует реализация FFTW и с поддержкой MPI, позволяющая работать с данными не помещающимися в память. Однако перегруппировка данных приводит к оверхеду, которого трудно избежать при in-place вычислении преобразований различных размеров.

3 Литература

[1] L. Rabiner, B. Gold, "Theory and application of digital signal processing" // Prentice Hall, New Jersey, 1975.

[2] Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. "Численные методы" // БИНОМ. Лаборатория знаний, Москва, 2008.

[3] M. Frigo, S. G. Johnson "FFTW Documentation" // fftw.org