Участник:Алексей Будюк/Метод Якоби вычисления собственных значений симметричной матрицы

Авторы описания: А.М. Будюк (общее и мат описание алгоритма), В.А. Сальников (информационный граф, вычислительное ядро алгоритма). В остальные разделы статьи вклад равноценный.

Метод Якоби вычисления собственных значений симметричной матрицы АВ
Последовательный алгоритм
Последовательная сложность	[math]O(n^3)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n^2)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Целый ряд инженерных задач сводится к рассмотрению систем уравнений, имеющих единственное решение лишь в том случае, если известно значение некоторого, так называемого, собственного значения системы. С задачами на собственные значения инженер сталкивается в различных ситуациях. Так, для тензоров напряжений собственные значения определяют главные нормальные напряжения, при динамическом анализе механических систем собственные значения соответствуют собственным частотам колебаний. При расчете конструкций собственные значения позволяют определять критические нагрузки, превышение которых приводит к потере устойчивости.
Таким образом, задача нахождения собственных значений и собственных векторов матриц (СЗВМ) является одной из основных задач для многих разделов физики. Одним из методов решения является метод Якоби. Этот метод позволяет привести матрицу к диагональному виду, последовательно, исключая все элементы, стоящие вне главной диагонали. В итоге, накопление в процессе преобразований произведения трансформационных матриц дает матрицу собственных векторов, в то время как диагональные элементы являются собственными значениями. К сожалению, приведение к строго диагональному виду, в общем случае, требует бесконечно большого числа шагов, так как образование нового нулевого элемента на месте одного из элементов матрицы часто ведет к появлению ненулевого элемента там, где ранее был нуль, так как при преобразовании затрагиваются и другие элементы матрицы. На практике метод Якоби рассматривают, как итерационную процедуру, которая в принципе позволяет с заданной точностью подойти к диагональной форме.
В случае симметричной матрицы [math]A[/math] действительных чисел преобразование выполняется с помощью ортогональных матриц [math]P[/math], полученных в результате вращении в действительной плоскости. Вычисления осуществляются следующим образом. Из исходной матрицы [math]A[/math] образуют матрицу [math]A_1[/math], при этом ортогональная матрица плоского вращения [math]P_1[/math] выбирается так, чтобы в матрице [math]A_1[/math] появился нулевой элемент, стоящий вне главной диагонали (обычно выбирается наибольший по модулю элемент). Затем из [math]A_1[/math] с помощью второй преобразующей матрицы [math]P_2,[/math] образуют новую матрицу [math]A_2[/math]. При этом [math]P_2[/math], выбирают так, чтобы в [math]A_2[/math] появился еще один нулевой внедиагональный элемент. Эту процедуру продолжают, стремясь, чтобы на каждом шаге в нуль обращался наибольший внедиагональный элемент. В итоге получаем некоторый бесконечный итерационный процесс, на каждом шаге которого преобразующаяся матрица становится всё более и более близкой к диагональной форме (в смысле уменьшения суммы квадратов всех своих недиагональных элементов). На практике, при решении задач, выбирается некоторая величина [math]\epsilon[/math], и итерационный процесс останавливается, когда наибольший по модулю внедиагональный элемент становится меньше [math]\epsilon[/math].

1.2 Математическое описание алгоритма

Пусть [math]A=(a_{ij})[/math] симметричная матрица, а [math]P(i,j,\theta)[/math] ортогональная матрица, называемая вращением Якоби, зависящая от параметра [math]\theta[/math], тогда итерационная последовательность строится следующим образом:

[math] A_k = P_k^TA_{k-1}P_k [/math]

Матрицы [math] A_i[/math] образуют итерационную последовательность симметричных матриц, сходящуюся к диагональной матрице из собственных значений [math]D[/math]. А так как

[math] A_k = P_k^TA_{k-1}P_k = P_k^TP_{k-1}^TA_{k-2}P_{k-1}P_k = ... = P^TA_1P [/math],

то матрицы вращений образуют матрицу из собственных векторов [math]P=P_kP_{k-1}..P_1[/math]. Матрица вращения [math]P(i,j,\theta)[/math] имеет следующий вид:

[math]P(i,j,\theta)=\begin{pmatrix} 1 & & & & & & 0 \\ &\ddots & & & & & \\ & & cos(\theta) & & -sin(\theta) & & \\ & & & \ddots & & & \\ & & sin(\theta) & & cos(\theta) & & \\ & & & & &\ddots & \\ 0 & & & & & & 1 \end{pmatrix} [/math]

Где синусы и косинусы стоят только на [math]i[/math] и [math]j[/math] позициях.
Если же мы произведём матричное умножение [math]P_k^TA_kP_k[/math], то в результате первого умножения [math]P_k^TA_k[/math] изменит только строки [math]i[/math] и [math]j[/math] матрицы [math]A_k[/math], в то время как [math]A_kP_k[/math] меняет только столбцы [math]i[/math] и [math]j[/math]. Таким образом изменённые элементы расположены только в строках и столбцах [math]i[/math] и [math]j[/math] матрицы [math]A_k[/math]. Поэтому логичнее вычислять именно эти элементы по следующим формулам (которые на самом деле и есть результат перемножения матриц), чем полностью перемножать матрицы:

[math] \begin{align} a_{ii}^{k+1}&=c^2a_{ii}^k-2sca_{ij}^k+s^2a_{jj}^k \\ a_{jj}^{k+1}&=s^2a_{ii}^k+2sca_{ij}^k+c^2a_{jj}^k \\ a_{ij}^{k+1}&=a_{ji}^{k+1}=(c^2-s^2)a_{ij}^k+sc(a_{ii}^k-a_{jj}^k)\\ a_{il}^{k+1}&=a_{li}^{k+1}=ca_{il}^k-sa_{jl}^k\\ a_{jl}^{k+1}&=a_{lj}^{k+1}=sa_{il}^k+ca_{jl}^k\\ a_{lm}^{k+1}&=a_{ml}^k,\\ \end{align} [/math]      [math] l,m\neq i,j [/math]

Приравнивая внедиагональный элемент к нулю, получаем формулы для параметра [math]\theta[/math]:

[math]r=ctg(2\theta)=\frac{c^2-s^2}{2sc}=\frac{a_{jj}-a_{ii}}{2a_{ij}}[/math]

[math]tg(\theta)=t=\frac{sign(r)}{|r|+\sqrt{1+r^2}}[/math]

[math]c=\frac{1}{\sqrt{1+t^2}}[/math]

[math]s=ct[/math]

Если [math]a_{jj}=a_{ii}[/math] то [math]\theta=\frac{\pi}{4}[/math]

1.3 Вычислительное ядро алгоритма

Основные вычислительные затраты:

1. Достаточно затратная операция сравнения в количестве [math]\frac{n(n-1)}{2}-1[/math] для нахождения максимума внедиагональных элементов и получения его индексов.
2. Пересчёт элементов массива, изменённых при вращении, в [math]i[/math] и [math]j[/math] строках и столбцах в количестве [math]4(n-1)[/math] по формулам, описанным выше.

1.4 Макроструктура алгоритма

На макроуровне выделяем 3 основных операции:

1. Выбор обнуляемого элемента (поиск максимального внедиагонального элемента). Осуществляется с помощью сравнений элементов [math]a_{ij} [/math] над диагональю в матрице [math]A[/math].
2. Вычисление параметров вращения. По формулам из пункта 1.2 вычисляются [math]sin(\theta)[/math] и [math]cos(\theta)[/math].
3. Применение вращения (пересчёт элементов матрицы). Пересчитываются элементы:

[math]\begin{align} a_{jm}^{(k+1)} &= a_{mj}^{(k+1)} = c \, a_{jm}^{(k)} - s \, a_{im}^{(k)} & m \ne j,i \\ a_{im}^{(k+1)} &= a_{mi}^{(k+1)} = s \, a_{jm}^{(k)} + c \, a_{im}^{(k)} & m \ne j,i, \end{align}[/math]

в количестве [math] (n-2) [/math] раза, а также вычисление элементов [math]a_{jj}^{(k+1)} [/math]   и   [math]a_{ii}^{(k+1)} [/math]:

[math]\begin{align} a_{ii}^{(k+1)} &= c^2\, a_{jj}^{(k)} - 2\, s c \,a_{ji}^{(k)} + s^2\, a_{ii}^{(k)} \\ a_{jj}^{(k+1)} &= s^2 \,a_{jj}^{(k)} + 2 s c\, a_{ji}^{(k)} + c^2 \, a_{ii}^{(k)} \end{align}[/math]

1.5 Схема реализации последовательного алгоритма

Выбираем желаемый уровень точности [math]\epsilon[/math].

1. В матрице [math]A_k, \;\; k=0,1,...[/math]   выбрать среди всех внедиагональных элементов(достаточно рассмотреть, например, только наддиагональные) максимальный по модулю [math]a^k_{i_kj_k},\;\; i_k\lt j_k[/math]   и запомнить его индексы.
2. Для выбранного [math]\epsilon[/math] проверяется условие: [math]|a^k_{i_kj_k}|\lt \epsilon[/math]. Если условие не выполнено, то перейти к п.3, иначе завершить процесс.
3. Для данного элемента матрицы вычислить параметры поворота [math]c=cos(\theta)[/math] и [math]s=sin(\theta)[/math] для матриц [math]P_k[/math].
4. Применить поворот: [math]A_{k+1}=P_k^TA_kP_k[/math], пересчитав элементы матрицы [math]A_k[/math] по формулам приведённым выше.
5. Перейти на п.1

1.6 Последовательная сложность алгоритма

1. Для поиска максимального элемента, как уже говорилось ранее, нам требуется [math]\frac{n(n-1)}{2}-1[/math] сравнений.
2. Сравнение для условия остановки.
3. Для вычисления параметров поворота: 3 деления, 4 умножения, 4 сложения(вычитания), 2 операции взятия корня.
4. Для пересчёта элементов матрицы: [math]4n+6[/math] умножений и [math]2n[/math] сложений.

Итого, перебирая в общем случае все [math]\frac{n(n-1)}{2}[/math] внедиагональные элементы матрицы, чтобы сократить сравнения, получаем сложность алгоритма [math]O(n^3)[/math], что в принципе соответствует сложности перемножения матриц.

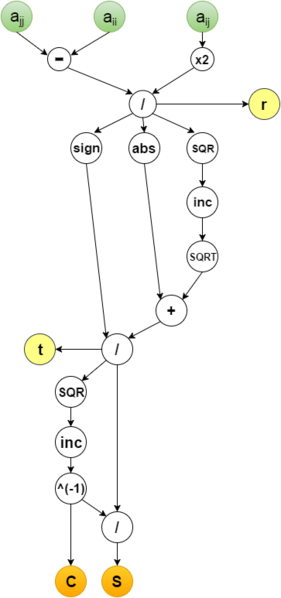
1.7 Информационный граф

Опишем алгоритм как аналитически, так и в виде рисунка.

Группе вершин A соответствует вычисление модуля максимума среди наддиагональных элементов.

Группе вершин B соответствует сравнение элемента [math]|a^k_{i_kj_k}|[/math] с заданным параметром [math]\epsilon[/math]. Если [math]|a^k_{i_kj_k}|\lt \epsilon[/math], то переходим к группе вершин C, иначе завершается работа алгоритма.

Группе вершин C соответствует вычисление параметров поворота [math]c=cos(\theta)[/math] и [math]s=sin(\theta)[/math] для матриц [math]P_k[/math].

Группе вершин D соответствует операция поворота матрицы [math]A_k[/math] по формулам пересчета элементов матрицы.

• 

  Рисунок 1. Граф итераций алгоритма

• 

  Рисунок 2. Структура вершины C с входными и выходными параметрами

• 

  Рисунок 3. Структура вершины D. Вершине E соответствует вычисление элементов [math]a_{il}[/math] и [math]a_{jl}[/math] в двух строках матрицы по формулам выше. Таких вершин на данном этапе [math]2*(n-2)[/math]. Вершине F соответствует вычисление элементов [math]a_{ii}[/math] и [math]a_{jj}[/math].

1.8 Ресурс параллелизма алгоритма

Наш алгоритм является итерационным и соответственно каждая итерация последовательна, что видно на информационном графе.

Рассмотрим одну итерацию:

1. На шаге вычисления параметров высота ярусно-параллельной формы(ЯПФ) равна 11, а ширина 3.
2. Основной ресурс параллелизма заложен на шаге пересчёта элементов матрицы. Ярус имеет ширину [math]2n-2[/math].    На [math]2n-4[/math] его узлах выполняется последовательно 2 умножения и 1 сложение(вычитание) для элементов [math]a_{im}^{(k+1)} = a_{mi}^{(k+1)}[/math]   и   [math]a_{jm}^{(k+1)} = a_{mj}^{(k+1)}[/math],   [math]m \ne i,j[/math]   и на 2 узлах последовательно 7 умножений и 2 сложения(вычитания) для элементов [math]a_{ii}^{(k+1)} [/math]   и   [math]a_{jj}^{(k+1)} [/math]. Таким образом, имея неограниченное количество процессоров, этот шаг выполняется за константное количество операций.

В итоге основная сложность параллельного алгоритма заключается в последовательном выполнении итераций в количестве [math]\frac{n(n-1)}{2}[/math]. В результате чего сложность получается [math]O(n^2)[/math], а по ширине ЯПФ [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: симметрическая матрица [math]A=(a_{ij})[/math].

Объём входных данных: матрица размера [math]n\times n[/math], но из-за симметричности достаточно хранить только диагональ и над/поддиагональные элементы и объём сокращается до   [math]\frac{n (n + 1)}{2}[/math].

Выходные данные: вектор собственных значений [math]\Lambda[/math] матрицы [math]A[/math].

Объём выходных данных: вектор размера [math] n [/math].

1.10 Свойства алгоритма

• Как было видно ранее, параллельный алгоритм не дал сильного выигрыша в сложности. Соотношение последовательной и параллельной сложности равняется [math]O(n).[/math]
• При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных также имеет порядок [math]O(n).[/math]
• Отметим, что для симметричной матрицы задача нахождение собственных значений симметричной матрицы является устойчивой.
• Касательно вопроса сбалансированности вычислительного процесса можно отметить, что умножений в 2 раза больше сложений(вычитаний). Обращения в память зависят от конкретной реализации, использование кешей, и т.д. Имеет место сбалансированность операций между параллельными ветвями алгоритма.
• Итерационный метод Якоби является недетерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных и параметра точности [math]\epsilon[/math].
• Степень исхода из вершины С на информационном графе образует пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы).

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости проводилось на на 1U сервере со следующими характеристиками:

• 2 x Intel® Xeon® Processor E5-2697 v2;
• 128GB RAM;

С параметрами запуска:

• Число процессоров [math]1,2,4,8,16,32,48[/math]
• Размер исходной матрицы [math]n\times n[/math], при [math]n=200,300,500,1000,1500,2000[/math]

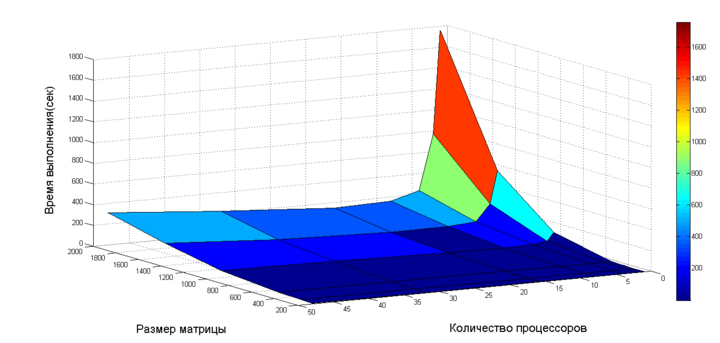
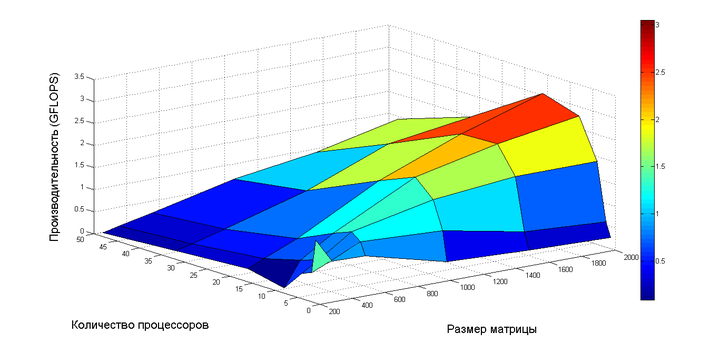
На следующих рисунках приведены графики времени выполнения и производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска

Рисунок 4. Зависимость времени выполнения от числа процессов и размера входной матрицы

Рисунок 5. Зависимость производительности от числа процессов и размера входной матрицы

2.7 Существующие реализации алгоритма

Готовая библиотека JACOBI_EIGENVALUE содержит последовательную реализацию алгоритма на С,С++,FORTRAN77,FORTRAN90,MATLAB,Python.

Параллельная реализация метода на платформе CUDA.

3 Литература

<references \>