Участник:Sagak/Алгоритм Ланцоша в арифметике с плавающей точкой

Автор: Айвазян Сагак Арамович

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша – итерационный метод , созданный Корнелиусом Ланцошем, для нахождения собственных значений и собственных векторов симметричной матрицы. Суть алгоритма в том, что он сводит частичную проблему собственных значений симметричной вещественной матрицы к полной проблеме собственных значений для симметричной трехдиагональной матрицы меньшей размерности. Алгоритм применяется к матрицам большой размерности, к которым не применимы никакие прямые методы. Есть множества вариантов этого алгоритма. Основные три вида : Алгоритм Ланцоша с точной арифметикой, Алгоритм Ланцоша в арифметике с плавающей точкой и Алгоритм Ланцоша с выборочной ортогонализацией. Алгоритм Ланцоша в арифметике с плавающей точкой учитывает округления, возникающие при вычислениях.

Алгоритм Ланцоша относится к методам аппроксимаций, которые применяют широко распространенную в математике процедуру Релея-Ритца к матричным вычислениям, посредством чего сводят исходную задачу к задаче гораздо меньшего размера, решив которую, получаем приближенные собственные значения и собственные векторы исходной задачи. Метод основан на применении процедуры Релея-Ритца к последовательности вложенных подпространств Крылова. Важной особенностью подпространства Крылова является трехдиагонольность ортогональной проекции на него исходной матрицы, что способствует тому, что процедура Релея-Ритца прорабатывает очень эффективно. Главными особенностями поведения алгоритмов метода Ланцоша являются потеря ортогональности векторов базиса и быстрая сходимость в области наибольших по значению собственных значений. Наиболее популярными средствами борьбы с потерей ортогональности векторов Ланцоша являются различные варианты переортогонализации: частичная, полная и выборочная.

Симметричность исходной матрицы позволяет хранить и вычислять чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций. Также алгоритм позволяет использовать так называемый режим накопления, обусловленный тем, что значительную часть вычислений составляют вычисления скалярных произведений.

Преимущество алгоритма заключается в том, что он дает приближение за конечное число шагов. Метод Ланцоша выигрывает в конкуренции таким прямым методам, как метод прямых или обратных итераций, [math]QR[/math] и [math]QL[/math] преобразования, методы вращений (вращения Якоби), которые потеряли значение как самостоятельные методы поиска собственных значений матриц большого размера. Также нужно заметить, что метод Ланцоша практически всегда эффективнее других методов аппроксимаций.

1.2 Математическое описание алгоритма

Исходные данные: положительно определённая симметрическая матрица [math]A[/math], вектор [math]b[/math], количество итераций [math]k[/math].

Вычисляемые данные: трехдиагональная матрица [math]T_k[/math](элементы [math]t_{ij}[/math]) размерности [math]k[/math].

Итак, пусть [math]A=A^t \in R^{n{\times}n}[/math], тогда

[math]T_k[/math][math]=Q_k^tAQ_k, [/math]

где [math]T_k[/math]-верхняя симметричная трехдиагональная матрица, [math]Q_k=[q_1,q_2,...,q_k][/math], столбцы которой образуют ортонормированный базис подпространства

Крылова [math]K_m(A,b)[/math] для заданной матрицы [math]A[/math] и вектора [math]b[/math].

Обозначим:

[math]\alpha_i=t_{i,i},i=1,k [/math]

[math]\beta_i=t_{i-1,i},i=2,k[/math]

Тогда матрица [math]T_k=\begin{bmatrix} \alpha_1 & \beta_2 \\ \beta_2 & \alpha_2 & \beta_3 &\\ &. & . & .\\ &&\beta_{k-1} & \alpha_{k-1} & \beta_k\\ &&&\beta_k & \alpha_k \end{bmatrix}[/math],

Записывая матричное равенство по-векторно, получим следующий алгоритм Ланцоша.

[math] \begin{align} q_1&=b/||b||,\beta_1=0,q_0=0. \\ z&=Aq_j, \\ \alpha_j&=q_j^Tz, \\ z&=z-\alpha_jq_j-\beta_{j}q_{j-1}, \\ \beta_{j+1}&=||z||,\\ q_{j+1}&=z/\beta_{j+1}, \quad j \in [1, k]. \end{align} [/math]

В точной арифметике на [math]j[/math]-ой итерации [math]z[/math] будет ортогонален векторам [math]q_1,q_2..q_{j-1}[/math], но к сожалению это свойство теряется из-за округлений в арифметике с плавающей точкой. Чтобы бороться с этим, проводится полная переортоганализация, что соответствует повторному проведению процесса ортогонализации Грамма-Шмидта [math]z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i.[/math] Однако добавление этих двух операций делает реализацию алгоритма Ланцоша гораздо дорогостоящей.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро последовательной версии алгоритма Ланцоша можно составить из операции умножения вектора на матрицу и процесса полной переортогонализации, именно на них приходится основное время работы алгоритма.

• 1. [math]Aq_p=( \sum\nolimits_{i=1}^na_{1i}q_{pi}, \sum\nolimits_{i=2}^na_{2i}q_{pi} ..., \sum\nolimits_{i=1}^na_{ni}q_{pi})[/math], как известно в операции задействуется [math]n^2[/math] умножений и [math]n(n-1)[/math]сложений.

• 2. [math]z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i, z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i,[/math] сложность переортогонализации:[math]k(k+1)n+2k[/math] умножений и [math]k(k+1)n+2+k[/math] сложений.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют множественные вычисления [math]n[/math] скалярных произведений на [math]p[/math]-ой итерации

[math]\sum\nolimits_{j=1}^na_{ji}q_{pi}[/math],

возникающие при умножение исходной матрицы [math]A[/math] на очередной вектор базиса [math]q_p[/math].

И [math]2k[/math] скалярных произведений необходимых для проведения процесса Грамма-Шмидта для ортогонализации текущего вектора [math]z[/math] со всеми построенными векторами базиса

[math]\sum\nolimits_{i=1}^nz_{i}q_{pi}[/math].

Для уменьшения ошибок округления режимом накопления в алгоритме рекомендуется использовать скалярное произведение не одинарной точностью, а с двойчной.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения метода следующая:

Сначала заполняем начальные значения.

[math] \begin{align} \\ & q_1=b/||b||,\\ & \beta_1=0,\\ &q_0=0, \\ \end{align} [/math]

где [math]b[/math]-произвольный вектор.

Далее выполняется основная процедура, которая строит ортонормированный базис подпространства Крылова для симметричной матрицы и трехдиагональную матрицу размерности [math]k[/math].

Для всех [math]j[/math] от [math]1[/math] до [math]k[/math] по нарастанию выполняются

[math] 1.z=Aq_j, [/math]

Вычисляем элемент, который будет находится на позиции [math]t_{j,j}[/math] конечной матрицы [math]T_k[/math],

[math] 2.\alpha_j=q_j^Tz, [/math]

Чтобы гарантировать ортогональность базиса на каждой итерации цикла два раза проводим полную переортогонализацию, использую процесс Грамма-Шмидта,

[math] 3.z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]

[math]4.z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]

После ортогонализации процедура продолжается следующим образом.

[math]5.z=z-\alpha_jq_j-\beta_{j}q_{j-1}, [/math]

Вычисляем элемент, который будет находится на позиции [math]t_{j,j+1}[/math] и [math]t_{j+1,j}[/math],

[math]6.\beta_{j+1}=||z||, [/math]

Если [math]\beta_{j+1}=0[/math], то алгоритм завершается.

[math]7.q_{j+1}=z/\beta_{j+1}.[/math]

В конце каждой итерации получаем очередной вектор [math]q_{j+1}[/math] базиса с единичной нормой, который ортогонален всем предыдущим векторам базиса,

и элементы [math]\alpha_j[/math], [math]\beta_{j+1}[/math] трехдиагональной матрицы размерности [math]k[/math] .

1.6 Последовательная сложность алгоритма

Для выполнения алгоритма Ланцоша в последовательном варианте требуется:

• [math]k[/math] вычислений квадратного корня,

• [math]k((n+1)^2+nk-1)[/math] сложений (вычитаний),

• [math]k((n+1)^2+2kn)[/math] умножений

Умножения и сложения (вычитания) составляют основную часть алгоритма.

1.7 Информационный граф

Опишем граф алгоритма в виде рисунка.

• Вершина черного цвета соответствует операции [math]Aq_j,[/math].
• Вершина красного цвета соответствует операции скалярного произведения [math]q_j^Tz[/math].
• Вершина сиреневого цвета соответствует операции [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math].
• Вершина желтого цвета соответствует операции [math]z-\alpha_jq_j-\beta_{j-1}q_{j-1}[/math].
• Вершина синего цвета соответствует операции [math]||z||[/math].
• Вершина зеленого цвета соответствует операции [math]z/\beta_j[/math].

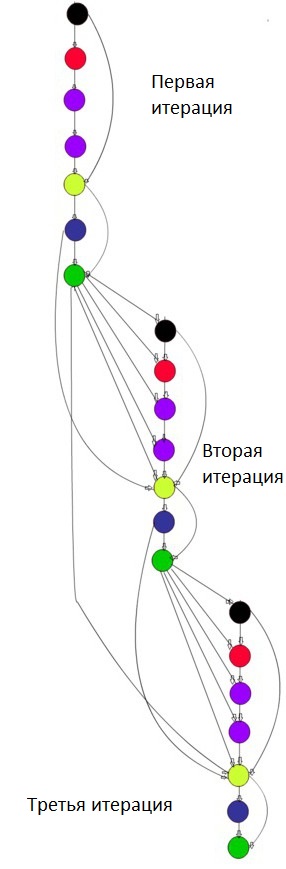Здесь показаны первые три итерации алгоритма, при больших итерациях граф строится аналогичным образом.

Отметим, что можно подробнее расписать первые четыре операции, первая из них является стандартной операцией умножения вектора на матрицу, вторая-скалярное произведение, третье и четвертя-сумма скалярных произведений. Именно эти операции содержат ресурс параллелизма.

1.8 Ресурс параллелизма алгоритма

Как видно из графа алгоритма каждая операция передает результат своих вычислений последующей операции. Соответственно никаких ресурсов параллелизма на уровне взаимодействия этих базовых операции нету. Они могут выполнятся строго последовательно. Однако, шесть операций содержат вычисления множества скалярных произведений.Стоит отметить, что в каждой итерации есть операция умножения матрицы на вектор, что представляет из себя [math]n[/math] информационно независимых скалярных произведений. Также хорошие возможности для параллельной реализации представляет повторная переортогонализация, так как на [math]j[/math] итерации обе операции ортогонализации вычисляют [math]j-1[/math] независимых скалярных произведения. Поскольку каждое вычисление скалярного произведения векторов длины [math]n[/math] требует выполнения [math]n[/math] операций умножения и [math]n-1[/math] операций сложения, его сложность [math]n[/math]. Если воспользоваться разделением данных по строкам, то в случае параллельных вычислений каждый процессор производит умножение только части (полосы) первого вектора на второй, размер этих полос равен [math]n/p[/math]

([math]p[/math]-количество процессоров). Следовательно, вычислительная сложность параллельного алгоритма скалярного произведения определяется выражением:[math]n/p[/math], а мультипликативная сложность всего алгоритма [math]O(n^2k+nk^2)/p)[/math]. При [math]p=n[/math] получаем [math]O(nk+k^2)[/math]. Однако этот метод не учитывает, то что есть скалярные произведения, которые могут вычисляться параллельно. Если учесть весь ресурс параллелизма можно получить сложность [math]O(k)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]),произвольный вектор ненулевой [math]b[/math], количество итераций [math]k[/math].

Дополнительные ограничения:

• [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math]..

Объём входных данных: [math]\frac{n (n + 3)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы).

Выходные данные: трехдиагональная симметрическая матрица [math]T[/math] (элементы [math]_{ij}[/math]), либо два вектора [math]a[/math] и [math]b[/math] размерности [math]k[/math].

Объём выходных данных: [math]2k[/math] (в силу трехдиагональности симметричности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.

1.10 Свойства алгоритма

Алгоритм не является устойчивым, так как из-за округлений ортогональность построенных векторов подпространства Крылова быстро теряется, вплоть до того, что некоторые из них становятся линейно зависимыми, что влечет к отсутствию приближения собственных векторов и собственных значений исходной матрицы. Именно для того, чтобы решить это проблему, проводится полная переортогонализация.

Количество операций умножения и количество операций сложения имеют один и тот же порядок, но они явно преобладают над операцией взятия корня. Также сбалансированы между собой арифметические операции и операции обращений в память. Алгоритм обрабатывает матрицу и вектора и считает множество скалярных произведений, следовательно обеспечивается хорошая сбалансированность операций между параллельными ветвями алгоритма. Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов равняется [math]O(n^2)[/math].

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных равняется [math]O(k)[/math]. Алгоритм недетерминированный, так как если в какой-то итерации [math]b_j=0[/math], то алгоритм останавливается. Также на недетерминированность может повлиять изменение порядка выполнения ассоциативных операций, в частности при вычислении скалярного произведения.

"Длинных" дуг в информационном графе нет, запись данных происходит предсказуемо(на каждом шаге заполняются следующие элементы выходных векторов), следовательно нет никаких потенциальных сложностей с размещением данных в иерархии памяти компьютера на этапе выполнения программы.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

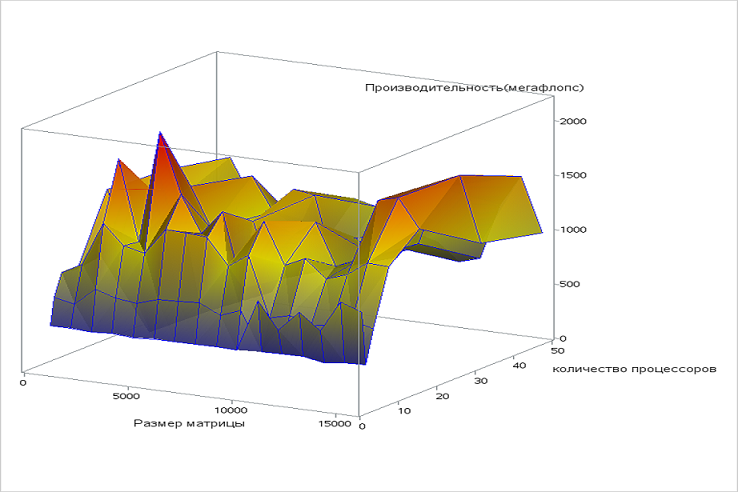
Исследование масштабируемости проводилось на 1U сервере со следующими характеристиками:

• 2 x Intel® Xeon® Processor E5-2697 v2;
• 128GB RAM;

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• Число процессоров [math]1,2,4,8,16,32,48[/math]
• Размерность матрицы [math][1000:16000][/math]
• Количество итераций [math]10[/math]

2.7 Существующие реализации алгоритма

NAG Library имеет множество процедур для решения система алгебраических уравнений и нахождения собственных значений, которые используют алгоритм Ланцоша.

http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R.

MATLAB содержит реализацию алгоритма в пакете Gaussian Belief Propagation Matlab Package.

http://www.cs.cmu.edu/~bickson/gabp/.

GraphLab имеет библиотеку, в которой есть огромное количество параллельных реализаций алгоритма Ланцоша

https://turi.com/products/create/open_source.html C++.

В LANSO/PLANSO есть параллельная версия алгоритма

http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran.

3 Литература

ДЖ.Деммель Вычислительная линейная алгебра. М.:Мир,2001

В. В. Вербицкий, В. В. Реут ВВЕДЕНИЕ В ЧИСЛЕННЫЕ МЕТОДЫ АЛГЕБРЫ 2015