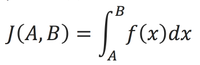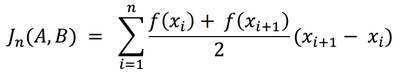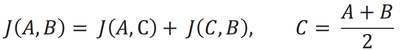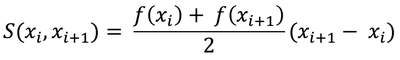Участник:Joinmek/Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки

Вычисление определенного интеграла с использованием адаптивно сгущающейся сетки
Последовательный алгоритм
Объём входных данных	[math]O(1)[/math]
Объём выходных данных	[math]O(1)[/math]

Основные авторы описания: Можарова В. А.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

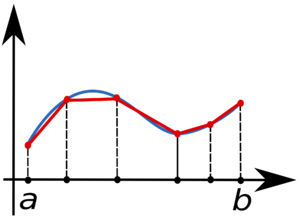
Основная идея большинства методов численного интегрирования состоит в замене подынтегральной функции на более простую, интеграл от которой легко вычисляется аналитически. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и парабол (Симпсона).

Рис.1. Метод трапеций

Чтобы посчитать определенный интеграл, участок интегрирования делится на отрезки, на которых подсчитывается значение новой (упрощенной) функции, после чего значения суммируются на всех отрезках. Но чтобы посчитать интеграл с определенной точностью, мы не можем заранее узнать, какие размеры отрезков, нужно использовать, т. к. это зависит от самой функции. Для этого используют адаптивное разбиение участка интегрирования: размер конкретного отрезка определяется во время подсчета значения функции на нем самом. Если заданная точность не была достигнута на данном отрезке, он рекурсивно разбивается на несколько новых и функция подсчитывается уже на них. Таким образом, выигрыш от применения рассмотренного алгоритма рекурсивного разбиения достигается за счет возможности использования сеток с разным числом узлов на разных участках интервала интегрирования.

1.2 Математическое описание алгоритма

Пусть у нас есть интеграл, который надо вычислить с точностью ε:

Предположим, что в результате адаптации сетки для данной функции, на отрезке [A, B] получилась сетка, содержащая n + 1 узел. Тогда согласно методу трапеций, можно численно найти определенный интеграл от функции f(x) на отрезке [A, B]:

Будем полагать значение J найденным с точностью ε, если выполнено условие:

где n₁ и n₂ - количество узлов, образующих две разные сетки. Пользуясь формулой

рекурсивно делим отрезки интегрирования до достижения на них заданной точности.

1.3 Вычислительное ядро алгоритма

Основное время работы алгоритма приходится на вычисление площадей на отрезках, получившихся в результате рекурсивного разбиения:

1.4 Макроструктура алгоритма

Алгоритм итеративный. Сначала значение текущего отрезка равно общему отрезу интегрирования. На каждой итерации:

1. На текущем отрезке считается приближенное значение интеграла

2. Текущий отрезок делится пополам, и на получившихся отрезках высчитываются новые интегралы

3. Если достигнута заданная точность, то

3.1 Добавить значение интеграла текущего отрезка к общему интегралу

3.2 Если стек пуст, то завершить алгоритм

3.3 Достать из стека отрезок и присвоить его значение текущему отрезку.

4. Иначе

4.1 Один из получившихся маленьких отрезков положить в стек

4.2 Текущему отрезку присвоить значение второго маленького отрезка

1.5 Схема реализации алгоритма

Для хранения отрезков интегрирования в данном алгоритме понадобится стек .

   sp=0  //    указатель вершины стека
   struct {
         A, B, fA, fB, s
   } stk[1000] 

У стека определен следующий набор операций:

1. PUT_INTO_STACK - положить элемент в стек

   #define PUT_INTO_STACK(A, B, fA, fB, s)
   {
       stk[sp].A=A
       stk[sp].B=B
       stk[sp].fA=fA
       stk[sp].fB=fB
       stk[sp].s=s
       sp++
   } 

2. GET_FROM_STACK - взять верхний элемент из стека

   #define GET_FROM_STACK(A, B, fA, fB, s)
   {
       sp--
       A=stk[sp].A
       B=stk[sp].B
       fA=stk[sp].fA
       fB=stk[sp].fB
       s=stk[sp].s
   }

3. STACK_IS_NOT_FREE - проверить стек на наличие в нем элементов

   #define STACK_IS_NOT_FREE (sp > 0)

   LocalStack (A, B)
   {
       // В переменной J храним ответ
       J=0
       // Вычисляем значение функции на границах интегрируемого отрезка
       fA = f(A)
       fB = f(B)
       // Вычисляем площадь с помощью метода трапеций
       sAB = (fA + fB) * (B - A) / 2
       while (1)
       {
           C = (A + B) / 2  // Находим середину отрезка
           fc = f(C)  // Вычисляем в середине значение функции
           // Считаем приближенное значение интеграла на получившихся отрезках
           sAC = (fA + fC) * (C - A) / 2
           sCB = (fC + fB ) * (B-C) / 2
           sACB = sAC + sCB
           if (|sAB - sACB| ≥ ε|sACB|) {  // Если заданная точность не достигнута
               PUT_INTO_STACK(A, C, fA, fC, sAC)  // то один из отрезков кладем в стек
               A = C  // и решаем задачу для оставшегося отрезка
               fA = fC
               sAB = sCB
           } else  // Если заданная точность достигнута
           {
               J += sACB  // то к общей сумме добавляем полученное число
               if (STACK_IS_NOT_FREE)  // если стек пуст, то цикл завершается - ответ получен
                   break 
               GET_FROM_STACK(A, B, fA, fB, sAB)  // иначе берем из стека новый отрезок
           } 
       }
       return J 
   }

1.6 Последовательная сложность алгоритма

Количество делений отрезков интегрирования зависит от сложности входной функции, поэтому нельзя оценить сложность данного алгоритма.

1.7 Информационный граф

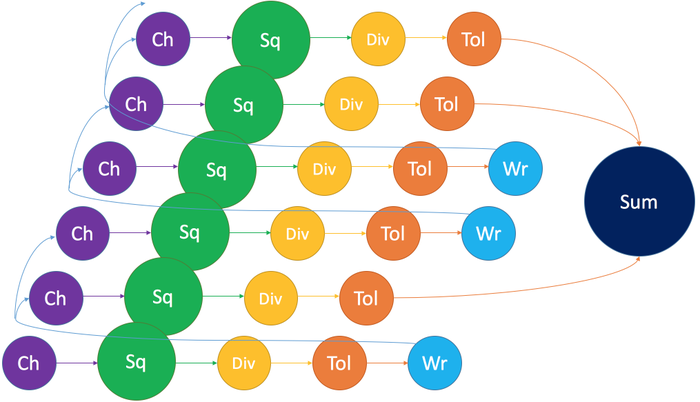
В параллельной версии алгоритма, появляется дополнительный глобальный стек, доступ к которому имеют все процессы. Он находится в общей памяти и так же содержит границы отрезков. Процессы обмениваются с ним данными, распределяя таким образом отрезки между собой. Когда в локальном стеке заканчиваются элементы, процесс обращается к глобальному стеку, чтобы получить их. Причем любой процесс может отдавать ему отрезки, если глобальный стек пуст в то время, как локальный имеет более одного отрезка. Изначально в глобальный стек помещается один отрезок, соответствующий участку интегрирования. Существуют реализации, где локальные стеки полностью отсутствуют, а все отрезки хранятся в глобальном стеке.

Рис.2. Информационный граф для алгоритма глобального стека. Ch - выбор отрезка интегрирования, Sq - вычисление площади на отрезке, Div - деление отрезка пополам, Tol - проверка достижения точности, Wr - запись отрезка в лок./глоб. стек, Sum - суммирование результатов

1.8 Ресурс параллелизма алгоритма

Сложность параллельного алгоритма нельзя оценить из-за зависимости от сложности интегрируемой функции так же, как и у последовательного алгоритма.

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается подынтегральная функция, пределы интегрирования и значение точности, с которой нужно посчитать заданный интеграл. На выходе: число – значение определенного интеграла.

1.10 Свойства алгоритма

1. Алгоритм адаптируется под сложность функции

2. Для каждого узла сетки значение функции высчитывается один раз

3. В параллельной версии алгоритма не требуется управляющий процесс

4. Алгоритм является детерминированным

5. Степень исхода вершины информационного графа равна 1, т. к. результат работы каждого процесса в дальнейшем используется только 1 раз.

6. В представленном параллельном алгоритме сбалансирована загрузка процессов, т. к. при завершении своих задач каждый процессор обращается за новыми в глобальный стек

7. Данный алгоритм является устойчивым

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Автором данной статьи была выбрана реализация RWTH AACHEN UNIVERSITY на языке C. Данная реализация не является масштабируемой, т. к. она основана на механизме общей памяти, а, значит, ограничена одним узлом.

Тогда было принято решение модифицировать данный алгоритм, разделив отрезок интегрирования на равные части, количество которых равно количеству запущенных процессов (Code). Каждый из них считает интеграл на своем участке, а затем отправляет результат нулевому процессу, на котором происходит суммирование.

Чтобы протестировать систему была выбрана функция sin(x). Вычисление интеграла запускается с разными значениями точности, чтобы пронаблюдать за изменением времени в зависимости от количества итоговых отрезков. Программа запускалась на Blue Gene. Использовался компилятор mpicc версии 4.1.2 с опцией -lm. Внутри программы использовалась стандартная библиотека языка C - math, которая была выбрана для подсчета функции синуса в заданных точках.

Рис.2. Зависимость времени работы алгоритма от числа процессов и заданной точности

Рис.3. Зависимость эффективности алгоритма от числа процессов и заданной точности

Масштабируемость:

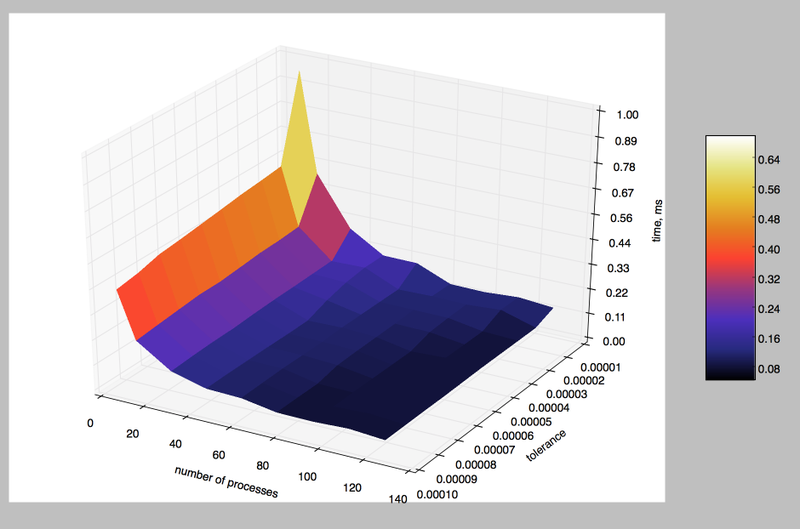
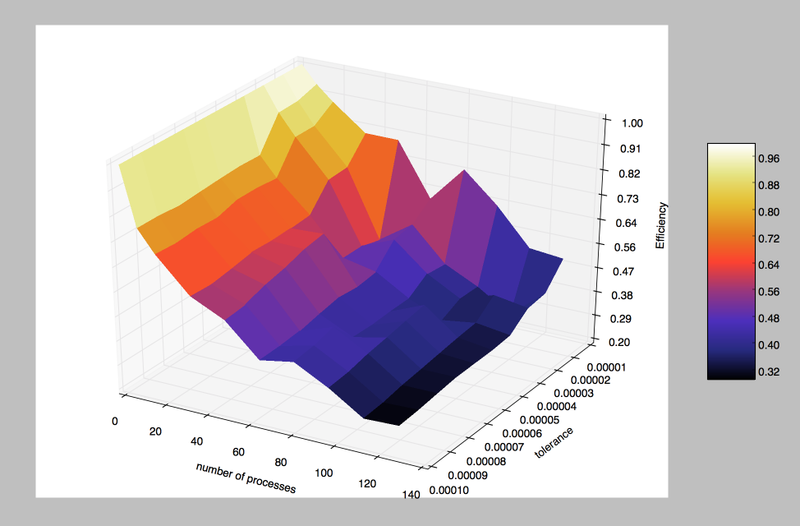
Система запускалась на количестве процессов от 8 до 128, начиная с 16 процессов шаг был равен 16. Точность градировалась от 0.00001 до 0.0001 с величиной шага 0.00001. Максимальная эффективность была достигнута на 8 процессах и равна 0.9389. Минимальная - на 128, ее величина 0.2914.

При увеличении числа процессов эффективность программы падает, т. к. увеличиваются накладные расходы, а также по причине того, что некоторым процессам попадаются более трудоемкие участки интегрирования, из-за которых остальным процессам приходится ожидать.

При фиксированном количестве процессов и увеличении сложности задачи (уменьшении точности), эффективность падает, но очень медленно.

2.7 Существующие реализации алгоритма

В России данный алгоритм реализован Якобовским М. В.

За границей осуществила реализацию компания RWTH Compute Cluster; группа исследователей во главе с Kamesh Arumugam; а также команда Berntsen, J.; Espelid, T. O.; and Genz, A..

3 Литература

<references \>