Участник:Vlamakarenko/Трассировка лучей

авторы: В.А.Макаренко, Р.А.Габдуллин

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

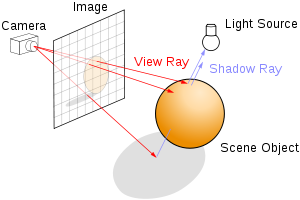
Трассировка лучей - это технология визуализации трехмерных сцен путем отслеживания обратной траектории лучей света (от наблюдателя к источнику). Достоинствами данного метода являются реалистичность итоговых изображений, возможность визуализации гладких объектов без аппроксимации полигональными поверхностями, простота реализации отражений, преломлений, взятия в фокус, реалистичного освещения; возможность параллельной обработки лучей.

1.2 Математическое описание алгоритма

1.2.1 Некоторые понятия из радиометрии

Энергетическая яркость

BRDF

Энергия излучения - энергия, переносимая оптическим излучением. Обозначается через  [math]Q[/math].

Поток излучения - мощность, переносимая оптическим излучением через какую-либо поверхность.  [math]\Phi = \frac{dQ}{dt}[/math].

Плотность потока излучения - отношение потока излучения, проходящего через малый участок поверхности, к площади этой поверхности.   [math]\frac{d\Phi}{dA}[/math],   где   [math]dA[/math] - дифференциал поверхности.

Облученность - отношение потока излучения, падающего на малый участок поверхности, к площади этой поверхности.   [math]E=\frac{d\Phi}{dA}[/math],   где   [math]dA[/math] - дифференциал поверхности.

Энергетическая светимость - отношение потока излучения, испускаемого малым участком поверхности, к площади этой поверхности.  [math]M=\frac{d\Phi}{dA}[/math],   где   [math]dA[/math] - дифференциал поверхности.

Сила излучения - мощность излучения источника света в некотором направлении. Равна отношению потока излучения, исходящего от источника, к малому телесному углу.   [math]I=\frac{d\Phi}{d\omega}[/math].

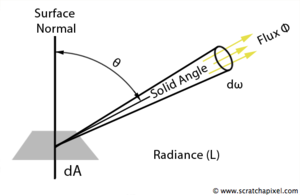
Энергетическая яркость - отношение потока излучения через малую площадку поверхности и распространяющегося в малом телесном угле, к площади проекции этой площадки на плоскость, перпендикулярную направлению распространения, и величине телесного угла.  [math]L=\frac{d^2\Phi}{dA\cdot d\omega \cdot \cos \theta}[/math]

Энергетическую яркость, падающую на элемент поверхности, будем назвать падающей яркостью и обозначать [math]L_i[/math]. Энергетическую яркость, отраженную элементом поверхности, будем называть отраженной яркостью и обозначать [math]L_o[/math].

Из определений следует, что:

1) [math]dE_i(\overline{p}, \overline{\omega}_i) = L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i[/math]
2) [math]E(\overline{p}) = \int_{\Omega_i} L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i \, d\omega_i[/math],  где интегрирование проводится по направлениям [math]\overline{\omega}_i[/math] таким, что [math](\overline{n}, \overline{\omega}_i)[/math] > 0,  то есть по полусфере.
([math]\overline{n}[/math] - нормаль к поверхности в точке [math]\overline{p}[/math],   [math]\Omega_i = 2\pi^{+}[/math]).

Пусть [math]\overline{p}[/math] - точка поверхности, [math]\overline{n}[/math] - нормаль в этой точке, [math]\overline{\omega}_i, \overline{\omega}_o[/math] - единичные вектора такие, что [math](\overline{n}, \overline{\omega}_i) \gt 0, \,\, (\overline{n}, \overline{\omega}_o) \gt 0 [/math]
Будем считать, что   [math]dL_o(\overline{p}, \overline{\omega}_o)[/math] пропорционален   [math]dE_i(\overline{p},\overline{\omega}_i)[/math]:
[math]dL_o(\overline{p}, \overline{\omega}_o) \sim dE_i(\overline{p},\overline{\omega}_i)[/math].
Функция   [math]f_r(\overline{p}, \overline{\omega}_i, \overline{\omega}_o) = \frac{dL_o(\overline{p}, \overline{\omega}_o)}{dE_i(\overline{p},\overline{\omega}_i)} = \frac{dL_o(\overline{p}, \overline{\omega}_o)}{L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i d\omega_i}[/math]   называется двулучевой функцией отражательной способности (BRDF).
В точке [math]\overline{p}[/math] может быть задано несколько BRDF - множество [math]\{f_{r_k}(\overline{p}, \overline{\omega}_i, \overline{\omega}_o)\}[/math].
Тогда итоговая BRDF просто равна сумме BRDF из этого множества: [math]f_r(\overline{p}, \overline{\omega}_i, \overline{\omega}_o) = \sum_k f_{r_k}(\overline{p}, \overline{\omega}_i, \overline{\omega}_o)[/math].
[math]L_o(\overline{p}, \overline{\omega}_o) = \int_{\Omega_i} f_r(\overline{p}, \overline{\omega}_i, \overline{\omega}_o) L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i d\omega_i[/math].   - уравнение отражений.
Важная часть алгоритма трассировки лучей - определить отраженную яркость по падающим яркостям, то есть посчитать этот интеграл. Обычно для вычисления интеграла применяют метод Монте-Карло.

1.2.1.1 Уравнение рендеринга

Уравнение рендеринга - это интегральное уравнение, которое определяет количество излученного в определенном направлении света как сумму отраженного и собственного излучения. Физической основой для уравнения рендеринга является закон сохранения энергии.

Уравнение отражений является частью уравнения рендеринга, поэтому остается только добавить собственное излучение объектов [math]L_e(\overline{p}, \overline{\omega}_o)[/math].

Уравнение рендеринга имеет вид [math]L_o(\overline{p}, \overline{\omega}_o) = L_e(\overline{p}, \overline{\omega}_o) + \int_{\Omega_i} f_r(\overline{p}, \overline{\omega}_i, \overline{\omega}_o) L_i(\overline{p}, \overline{\omega}_i)\cos \theta_i d\omega_i[/math].

По сути, алгоритмы рендеринга, в том числе и трассировка лучей, занимаются поиском приближенного решения уравнения рендеринга.

1.2.1.2 Поиск приближенного решения уравнения рендеринга

Введем оператор поиска первого пересечения. [math]r_c(\overline{p}, \overline{\omega})[/math] - оператор, который находит точку первого пересечения с объектами луча, выпускаемого из точки [math]\overline{p}[/math] по направлению [math]\overline{\omega}[/math].

Воспользуемся предположением, что количество излучения, распространяющегося вдоль одной прямой одинаково в любой точке прямой. Тогда:

[math] L_i(\overline{p},\overline{\omega}_i) = L_o(r_c(\overline{p}, \overline{\omega}_i), -\overline{\omega}_i) [/math].

и уравнение рендеринга превратится в уравнение Фредгольма второго рода

[math] L_o(\overline{p},\overline{\omega}_o) = L_e(\overline{p},\overline{\omega}_o) + \int_{\Omega_i} f_{r}(\overline{p},\overline{\omega}_i,\overline{\omega}_o)L_o(r_c(\overline{p}, \overline{\omega}_i), -\overline{\omega}_i) \cos\theta_i d\omega_i [/math].

Обозначим интеграл в правой части как [math] K \circ L_o [/math]. Тогда уравнение рендеринга перепишется, как

[math] L_o = L_e + K \circ L_o [/math].

Искать решение будем итерационным методом: выберем какое-либо начальное приближение [math] L_{o}^{(0)} [/math]. Найдем значение правой части [math]L_o^{(1)} = L_e + K \circ L_o^{(0)}[/math], воспользуемся им для поиска следующего приближенного решения [math]L_o^{(2)} = L_e + K \circ L_o^{(1)} = L_e + K \circ ( L_e + L_o^{(0)} ) = L_e + K \circ L_e + K^2 \circ L_o^{(0)} [/math] и т.д.

В конечном итоге получим, что [math]L_o = \sum \limits_{n=0}^\infty K^n \circ L_o^{(0)}[/math].

Этот метод называется методом последовательных приближений.

1.2.2 Определения

Камера и видовая плоскость

Объект - поверхность в трехмерном пространстве.
Материал объекта - множество BRDF.
Сцена - четверка {камера, объекты, источники света, видовая плоскость}.

1.2.2.1 Камера

Камера - "виртуальный глаз", через который мы видим объекты сцены.

Камера задается положением в пространстве и ортонормированным базисом [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] (локальная система координат). [math]\overline{u}_c[/math] направлен вправо относительно наблюдателя, [math]\overline{v}_c[/math] - вверх, [math]\overline{w}_c[/math] - на наблюдателя. Таким образом, [math](\overline{u}_c, \overline{v}_c, \overline{w}_c)[/math] - правая тройка векторов. Вектор направления камеры в своей системе координат: [math](0, 0, -1)[/math].

1.2.2.2 Видовая плоскость

Перед камерой на расстоянии [math]d[/math] поставим пиксельную сетку [math]w \times h[/math] с размером пикселя [math]s \times s[/math] так, чтобы камера была направлена в ее центр. Итоговое изображение будет получено из этой сетки покраской пикселей в нужный цвет.

[math]p(i, j)[/math], где [math]i=\overline{0,h-1}, \quad j=\overline{0,w-1}[/math] - пиксел [math]i[/math]-ой строки снизу [math]j[/math]-го столбца слева.

Заметим, что с увеличением [math]d[/math] уменьшается угол обзора, а [math]s[/math] влияет на масштаб.

1.2.2.3 Источники света

Типы источников света:
1) Point light - точка, излучающая свет одиноково во всех направлениях.
2) Directional light - бесконечно удаленный источник света, задается единичным направлением на себя.
3) Area light - объект, излучающий свет одинаково во всех направлениях.

1.2.3 Алгоритм трассировки лучей

1.2.3.1 Генерация луча

Перед камерой на расстоянии [math]d[/math] поставим пиксельную сетку [math]w \times h[/math] с размером пикселя [math]s \times s[/math] так, чтобы камера была направлена в центр сетки. Итоговое изображение будет получено из этой сетки покраской пикселей в нужный цвет.

Пусть [math]p(i, j)[/math], где [math]i=\overline{0,h-1}, \quad j=\overline{0,w-1}[/math] - пиксел [math]i[/math]-ой строки снизу [math]j[/math]-го столбца слева. Проведем пучок лучей из камеры через пиксел в локальной системе координат камеры. Начало каждого луча в точке [math]\overline{pos}=(0,0,0)[/math]. Найдем вектора направления [math]\overline{dir}_n[/math]:

[math]\overline{dir}_n.x = s \cdot (j + \delta_n.x -\frac{w}{2} + \frac{1}{2}) [/math]

[math]\overline{dir}_n.y = s \cdot (i + \delta_n.y -\frac{h}{2} + \frac{1}{2}) [/math]

[math]\overline{dir}_n.z = d[/math],

где [math] \delta_n = (\delta_n.x, \delta_n.y) \in [0;1]^2[/math] - смещения начала n-ого луча.

Нормируем вектора [math]\overline{dir}_n[/math] и переведем лучи в глобальную систему координат.

1.2.3.2 Пересечение луча с объектами сцены

Все точки луча [math]ray(\overline{p}, \overline{d})[/math] можно представить в виде:

[math]h(x,y,z)=\overline{p}+t \cdot \overline{d}, \quad t \in [0;\infty) [/math].

Луч пересекает объект [math]O_i[/math] тогда и только тогда, когда [math]t_i = \inf\{t \gt 0 \, | \quad \overline{p}+t \cdot \overline{d} \in O_i\} \, \lt \infty[/math]

Если луч пересекает объект [math]O_i[/math], то [math]h_i(x,y,z) = \overline{p}+t_i \cdot \overline{d}[/math] - их первое пересечение, [math]t_i[/math] - расстояние от начала луча до точки пересечения.

1.2.3.3 Вычисление энергитической яркости [math]L_o[/math], выходящей из точки пересечения

Найдем [math]T = \{t_i\}[/math] - параметры пересечения с объектами (см. предыдущий пункт).

[math]t_{min} = \min \{t_i\}, \quad O_{min} = \{O_i | t_i = t_{min}\}[/math]

Если [math]t_{min} = \infty[/math], то луч не пересекает ни один объект и нужно покрасить соответствующий пиксел в черный цвет (цвет фона).

Если [math]t_{min} \lt \infty[/math], то нужно найти выходящее излучение (цвет) из точки пересечения в камеру. Выходящее излучение зависит от свойств материала объекта и входящего излучения в точку пересечения.

Чтобы вычислить входящее излучение, находится приближенное значение интеграла [math] \int_{\Omega_i} f_{r}(\overline{p},\overline{\omega}_i,\overline{\omega}_o)L_o(r_c(\overline{p}, \overline{\omega}_i), -\overline{\omega}_i) \cos\theta_i d\omega_i [/math] методом Монте-Карло.

Заметим, что каждый луч необходимо продолжить в некотором направлении(а не создавать новый пучок), так как необходимое количество лучей для численного интегрирования можно заранее сгенерировать в камере.

Таким образом, алгоритм моделирует обратное движение пучка лучей света, который пришел в камеру. Пучок лучей движется из камеры и, сталкиваясь с объектами, распространяется в пространство в случайных направлениях, согласно свойствам материалов объектов.

1.2.4 Улучшение визуальных качеств изображения

Заметим, что чем больше лучей выпускается через каждый пиксел изображения, тем лучше получается картинка.

1.3 Вычислительное ядро алгоритма

Основные вычисления связаны с поиском пересечения луча с объектами сцены.

1.4 Макроструктура алгоритма

Для каждого пикселя изображения генерируется пучок лучей, проходящих через этот пиксел.

Для каждого луча находится точка первого пересечения с объектами сцены, расчитывается входящие излучения и на основе этого - итоговое выходящее.
Для упрощения модели разобьем входящее излучение на прямое и непрямое.
Прямое излучение - излучение, приходящее в точку непосредственно от источников света.
Непрямое излучение состоит из отраженного от других объектов сцены света.

После этого цвет усредняется по всем лучам, проходящим через данный пиксел.

1.5 Схема реализации последовательного алгоритма

Здесь приведен псевдокод ключевых моментов алгоритма.

//Покраска пикселей изображения

    for (uint r = 0; r < h; r++) //строки
    {
        for (uint c = 0; c < w; c++) //столбцы
        {
            image(r,c) = renderPixel(r, c); //вычисляем цвет в пикселе
        }
    }

    //renderPixel(r, c)

    pixel_color = {0,0,0};

    for (uint j = 0; j < num_rays_per_pixel; j++)
    {
        pp = generatePoint(); //генерируем произвольное смещение внутри пикеля

        //вычисляем координаты точки на полотне
        x = s * (c - 0.5 * w + pp.x);
        y = s * (r - 0.5 * h + pp.y);

        //cоздаем луч
        Ray ray({0,0,0}, normalize({x,y,-d}));
        Ray worldRay = convertToWorldCoords(ray);
        
        pixel_color += traceRay(worldRay, 0) * 1.0 / num_rays_per_pixel; //вычисляем цвет для каждого луча и усредняем
    }

    //traceRay(ray, depth)

    if (depth > max_depth) //превысили максимальную глубину луча, дальше не идем
    {
        return black; //возвращаем черный цвет
    }

    Intersection is = hitObjects(ray); //нашли первое пересечение с объектами сцены и записали информацию о нем в is:
                                       //материал объекта, расстояние, нормаль и т. п.

    if (is) //если есть пересечение
    {
        is.ray = ray; //запомнили луч
        is.depth = depth; // и глубину

        return shade(is); //расчитали цвет в точке пересечения в зависимости
                          //от материала объекта, используя информацию о пересечении
                                        
    }

    return getBackgroundColor(ray); //вернули цвет фона

//shade(is)

//цвета
direct_illumination = {0,0,0}; //прямое излучение
indirect_illumintaion = {0,0,0}; //непрямое излучение

for (uint i = 0; i < light_count; i++)
{
    if (light[i].isVisible(is)) //если источник света виден из точки пересечения
    {
         direct_illumination = getIllumination(light[i], is); //рассчитываем прямое излучение от i-го источника света
    }
}


if (isReflective(is.object))
{
      indirect_illumination = traceRay(reflecedRay(is.ray), is.depth + 1);
}

//зная входящее излучение, расчитываем выходящее в зависимости от свойств материала объекта
//...

1.6 Последовательная сложность алгоритма

Вычислим последовательную сложность алгоритма в терминах пересечения луча с объектами сцены.

[math]w[/math] - ширина полотна

[math]h[/math] - высота полотна

[math]depth_{max}[/math] - максимальная глубина луча в рекурсии

[math]N_{obj}[/math] - количество объектов сцены

[math]N_{lights}[/math] - количество источников света сцены

[math]N_{rays}[/math] - число лучей на один пиксел

На каждой итерации ищется пересечение луча со всеми объектами: [math]O(N_{obj})[/math]

После нахождения точки пересечения, выясняется, виден ли каждый источник света из этой точки. Для этого нужно найти первое пересечение теневого луча (начало в точке пересечения, направлен к источнику света) и сравнить расстояние до точки пересечения с расстоянием до источника света. Для всего этого требуется [math]O(N_{lights} \cdot N_{obj})[/math] операций.

Для каждого луча понадобится [math]O(depth_{max}(N_{obj} + N_{obj} \cdot N_{lights})) = O(depth_{max}\cdot N_{obj} \cdot N_{lights})[/math] операций.

Всего лучей, выходящих из камеры [math]w \cdot h \cdot N_{rays}[/math].

В итоге получаем [math]O(depth_{max}\cdot N_{obj} \cdot N_{lights} \cdot w \cdot h \cdot N_{rays})[/math] операций.

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается описание сцены (описание камеры, видовой плоскости, объектов и их материалов, источников света).
Выходные данные алгоритма - готовое изображение.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Реализация с помощью MPI

Размер изображения 700 на 700 пикселей, 256 лучей на пиксел, глубина рекурсии 3.
Сцена:

Число процессов	Время (с)
2	505.963
4	314.106
8	185.988
16	86.771
32	45.171
64	25.555
128	13.962
256	8.793
512	6.954

2.7 Существующие реализации алгоритма

RenderMan

V-Ray

NVIDIA IRay

NVIDIA mental ray

Hydra Renderer

3 Литература

Scratchapixel 2.0 - http://www.scratchapixel.com/

http://www.raytracegroundup.com/

HydraRenderer - http://www.raytracing.ru/

4 Полученные изображения

• 
• 
• 
• 
• 
•