Участница:V/Вычисление статистик квадрата норм разностей спектральных проекторов случайных матриц
Основные авторы описания: В.С.Шумовская
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
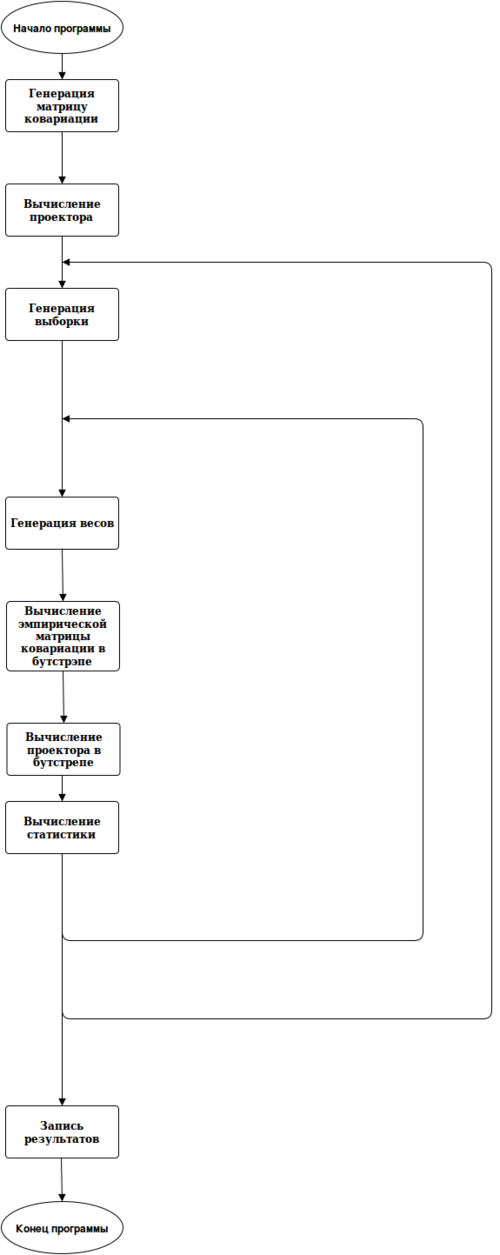
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Пусть [math]X_{1},\dots, X_{n}[/math] -- независимые и нормально распределенные случайные вектора в [math]\R^p[/math] с нулевым средним и матрицей ковариацией [math]\Sigma[/math], она лежит в [math]\R^{pxp}[/math] и такая, что ее собственные значения быстро убывают, т.е. 3-5 больших, а остальные, к примеру, в диапазоне от 1 до 3.
К этой выборке применим бутстрэп и вычислим в мире бутстрэпа [math]M[/math] матриц ковариаций сигма [math]\Sigma^{o}_{j}, j = 1,\dots,M.[/math]
Далее фиксируем [math]r[/math], обозначим за [math]P_{r}, P^{o}_{j}, j = 1,\dots,M[/math] - проекторы на r-ое подпространство и вычислим следующие статистики:
[math]S^{o}_{j} = ||P_{r} - P^{o}_{r}||^{2}_{2}[/math]
Задача -- вычислить большое количество этих статистик для визуализации их распределения.
1.2 Математическое описание алгоритма
- Генерация матрицы ковариации.
- Возьмем нужный нам набор собственных значений и поместим их на диагонали матрицы [math]\Lambda.[/math]
- Далее генерируем базис [math]p[/math]-мерного пространства и поместим его в матрицу [math]U.[/math]
- Тогда [math]\Sigma = U\Lambda U^{T}.[/math]
- Проделываем следующий цикл N раз:
- Генерация векторов [math]X[/math] ~ [math]N(\theta, \Sigma).[/math]
- Проделываем следующий цикл M раз:
- Генерация весов [math]w[/math] ~ [math]N(1, 1).[/math]
- Вычисление матриц ковариаций в бутстрэпе [math]\Sigma^{o} = \frac{1}{n}\sum_{k = 1}^{n}w_{k}X_{k}X^{T}_{k}. [/math]
- Вычисление собственных векторов [math]u_{1},\dots,u_{p}[/math] (в порядке убывания).
- Вычисление проекторов (считаем, что одномерные) по формуле [math]u = u_{r}u^{T}_{r}.[/math]
- Вычисление статистик [math]S^{o} = ||P_{r} - P^{o}_{r}||^{2}_{2}.[/math]
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на работу с матрицами (присутствует очень много умножений).
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
Явную формулу сложности последовательного алгоритма выписать не представляется возможным из-за огромного количества матричных операций из библиотеки MKL.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
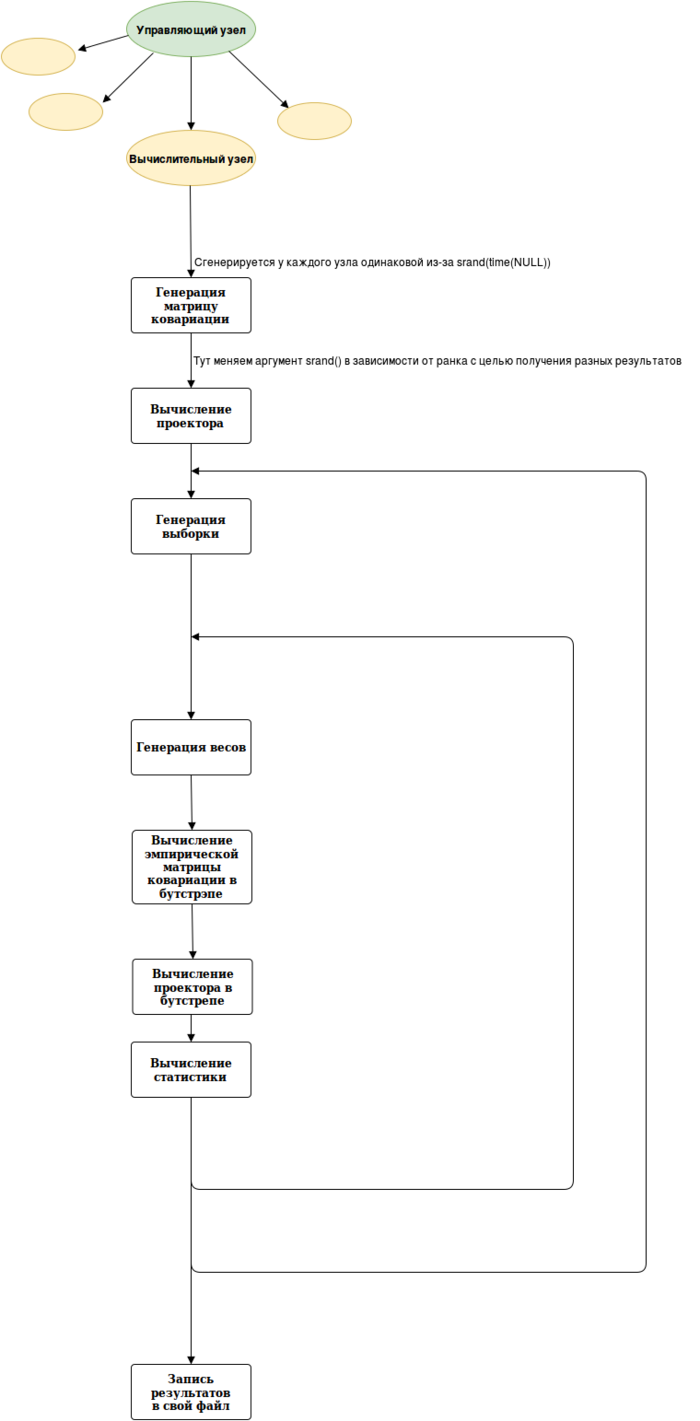
В принципе, параллельный алгоритм не сильно отличается от схемы последовательного алгоритма, но внешний цикл будет выполняться уже не условные N раз, а N деленное на число вычислительных узлов, поэтому программа будет работать быстрее. Так же на каждом узле параллельно вычисляются внутри узла многие операции (умножение матриц и т.д.)
1.9 Входные и выходные данные алгоритма
1.9.1 Входные данные
- Размерности матриц
- Количество повторений циклов
- Собственные значения
Эти параметры меняются в коде
1.9.2 Выходные данные
От каждого вычислительного узла будет получена матрица значений статистик
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Для исследования масштабируемости были проведены серии тестов с различным числом узлов (в степенях 2). Чем больше узлов, тем меньше загруженность каждого, если хотим получить одинаковый совокупный объем данных, а, следовательно, программа выполняется быстрее.
График для фиксированных n = 100, p = 10.
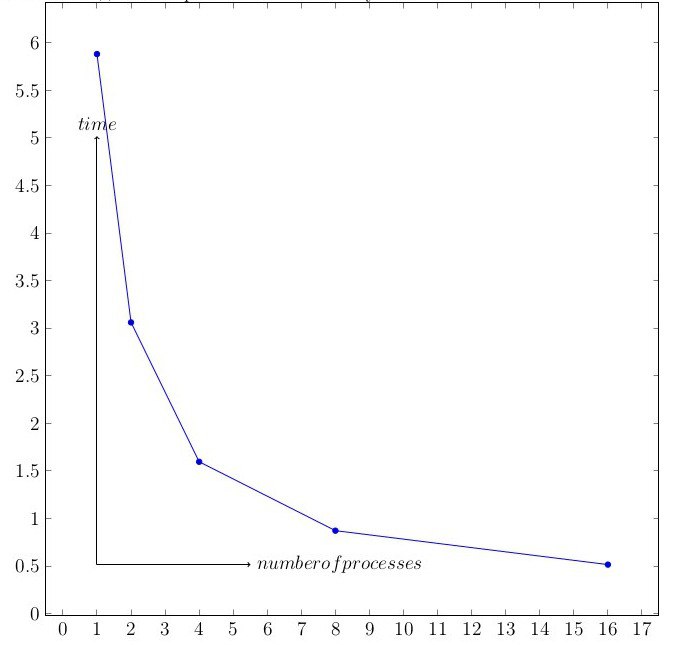
Все тесты проводились на суперкомпьютере Ломоносов. Характеристики вычислительного кластера: link.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
ваыва
3 Литература
ываыва