Участник:Евгений Раев/Построение матрицы Адамара произвольного размера
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 01.12.2016 Данная работа соответствует формальным критериям. Проверено Sleo. |
| Построение матрицы Адамара произвольного размера | |
| Последовательный алгоритм | |
| Последовательная сложность | O(n*(2^{n})^2)) |
| Объём входных данных | 1 |
| Объём выходных данных | (2^n)^2 |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(n) |
| Ширина ярусно-параллельной формы | O((2^n)^2) |
Работу выполнил студент 611 группы Раев Евгений.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Матрица Адамара H — это квадратная матрица размера n×n, составленная из чисел 1 и −1, столбцы которой ортогональны, так что справедливо соотношение
- H \cdot H^T = n \cdot E_n,
где E_n — это единичная матрица размера n. Матрицы Адамара применяются в различных областях, включая комбинаторику, численный анализ, обработку сигналов.
Матрица оператора Адамара имееет вид
- \begin{align} H = \frac{1}{\sqrt2} &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}
Соответственно, существует итерационная формула нахождения матриц Адамара, через тензорное произведение матрицы оператора Адамара на матрицу Адамара меньшего порядка:
- H_n = H_{1} \otimes H_{n-1}, где знак \otimes означает тензорное произведение.
Мы будем использовать в дальнейшем нормализованную матрицу оператора Адамара, без коэффицента (для удобности вывода):
- \begin{align} H = &\begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \end{align}
Представим пример высчитывания матриц Адамара:
- H_{0} = 1,
- H_{1} = H_{1} \otimes H_{0} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes 1 = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix},
- H_{2} = H_{1} \otimes H_{1} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} = \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix}
- H_{3} = H_{1} \otimes H_{2} = \begin{pmatrix}\begin{array}{rr} 1 & 1\\ 1 & -1 \end{array}\end{pmatrix} \otimes \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{pmatrix} = \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1\\ 1 & 1 & 1 & -1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & 1 & -1 & 1 & -1 & 1\\ 1 & 1 & -1 & 1 & -1 & -1 & 1 & 1\\ 1 & -1 & -1 & -1 & -1 & 1 & 1 & -1\\ \end{array}\end{pmatrix}
Таким образом, получаем последовательность матриц Адамамра размерностью 2^n
H^{\otimes n} = H_1 \otimes ... \otimes H_1 (Описано в[1]).
1.2 Математическое описание алгоритма
Тензорное произведение довольно затратно для реализации на вычислительной технике (необходимо хранить в памяти матрицу предыдущего порядка), поэтому существует формула для определения элемента матрицы Адамара по его индексам:
- H_{i,j} = (-1)^{\sum ij}, где i и j - битовые представляения значений индексов, а i j - побитовое умножение. (Описано в [2])
То есть, знак элемента матрицы Адамара зависит от количества едининц в побитовом произведении индексов - если это число чётное - то знак положительный, если нечётное - отрицательный.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро расчете элементов матрицы Адамара это вычисление элемента матрицы Адамара по его индексам:
- H_{i,j} = (-1)^{\sum i j}
Данная операция независима для каждого элемента, соответственно именно она подлежит распараллеливанию.
1.4 Макроструктура алгоритма
В вычислительном ядре используется операция опеределения четности суммы значачих единиц в результате побитового умножения двух чисел.
1.5 Схема реализации последовательного алгоритма
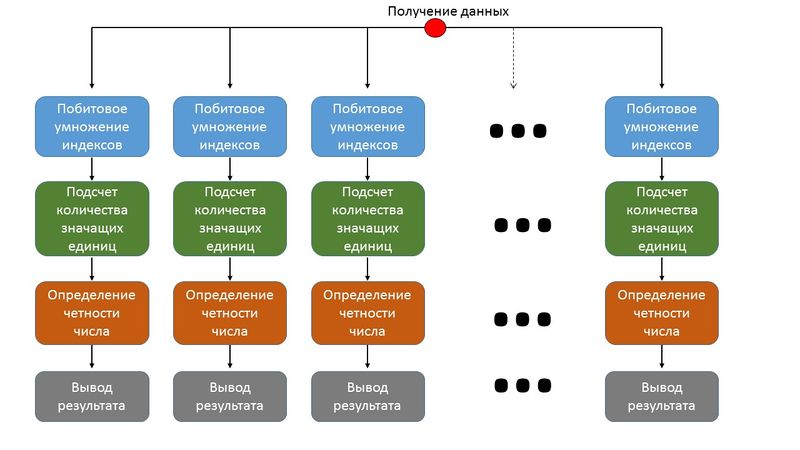
Последовательность исполнения метода следующая:
1. Определение индексов находимого элемента матрицы Адамара: i и j.
2. Побитовое умножение индексов : res = ij.
3. Подсчет количества значащих единиц в res: count = \sum res.
4. Получение знака элемента по его четности: sign = (-1)^{count}.
Данному алгоритму соответствует приведенный ниже код на языке С++:
#include <iostream>
#include <cmath>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
int get_sign(int i, int j) //Get sign Hadamard matrix's element by indices
{
int res = i & j;
int count;
for (count=0; res; res>>=1)
{
if (res & 1)
count++;
}
if (count & 1 ==1)
return -1;
else
return 1;
}
int print_HadamardMatrix(int N) //print Hadamard matrix 2^n size
{
int matr_size(pow(2,N));
for (int i = 0; i < matr_size; i++)
{
for (int j = 0; j < matr_size; j++)
{
if (get_sign(i,j)==1)
cout <<" 1 ";
else
cout <<"-1 ";
}
cout << endl;
}
cout << endl;
return 0;
}
int main(int argc, const char * argv[])
{
if(argc!=2)
{
printf("Matrix size missing\n");
return 1;
}
int N(atoi(argv[1]));
print_HadamardMatrix(N);
return 0;
}
1.6 Последовательная сложность алгоритма
Построение матрицы Адамара порядка 2^n требует рассчета (2^{n})^2 элементов матрицы. Это включает в себя:
1. (2^{n})^2 побитовых умножений индексов элемента i \& j.
2. Операция определения значащих единиц, состоит из последовательных сдвигов и умножений на 1. В худшем случае, если мы будет рассчитывать элемент с координатам (2^n-1,2^n-1) будет произведено n операций сдвига (так как число 2^n-1 кодируется n битами), и n операций умножения на 1 (для определения значащей единицы). То есть не более чем 2\cdot n\cdot(2^{n})^2 операций на данном шаге.
3. (2^{n})^2 побитовых умножений количества значащих единиц из предыдущего пункта с 1 для определения четности числа.
Следовательно, общая последовательная сложность алгоритма, равна (2^{n})^2 +2\cdot n\cdot(2^{n})^2 + 2^(2^{n})^2, то есть (2^{n})^2(2+2n), или O(n*(2^{n})^2))
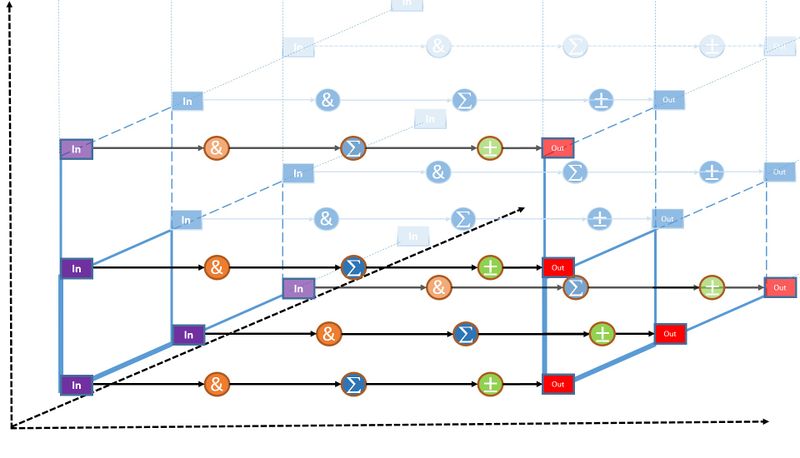
1.7 Информационный граф
На рисунке ниже изображен информационный граф алгоритма. Всего возможно (2^n)^2 параллельных ветвей, так как каждый элемент матрицы может считаться независимо друг от друга.
1. Операция \& - побитовое умножение индексов.ij, где i и j соответствующие координаты элемента h_{kl};
2. Операция \sum -подсчет количества значащих единиц. Состоит из последовательных сдвигов и побитового умножения с 1.
3. Операция \pm - определение четности количества значащих единиц. Состоит из побитового умножения количества значащих единиц с 1.
1.8 Ресурс параллелизма алгоритма
Для построения матрицы Адамара необходимы операции сдивга и побитового умножения. Расчет каждого элемента независим друг от друга, следовательно расчет каждого элемента будет являться параллельной ветвью (как видно на информационном графе). При расчете элемента все операции внутри параллельной ветви выполняются последовательно, ожидая окончания предыдущей.
Основной вклад в высоту ярусно-параллельной формы вносит 2 шаг, осуществляющий подсчет количества значащих единиц.
Ширина ярусно-параллельной формы будет равна O((2^n)^2) - количество рассчитываемых элементов. Высота ярусно-параллельной формы будет равна O(2+2n)=O(n)
1.9 Входные и выходные данные алгоритма
Входные данные: Одно натуральное число n. Данный алгоритм на основе этого числа строит матрицу Адамара H_n размерности 2^{n}\times 2^{n}.
Объём входных данных: 1 (число n).
Выходные данные: 2^{n}\cdot 2^n чисел, которые представляют собой элементы H_{i,j} матрицы Адамара H_{n} размерности 2^{n}\times 2^{n}. Вообще говоря, в силу симметричности матрицы Адамара, можно хранить только половину от этих данных, но алгоритм в статье не предполагает такой оптимизации).
Объём выходных данных: (2^{n})^2.
1.10 Свойства алгоритма
- Соотношение последовательной и параллельной сложности можно определить как отношение высоты ярусно-параллельной формы и общей последовательно сложности, то есть \frac{ (2+2n)(2^n)^2 }{2+2n} = (2^n)^2 . Таким образом, соотношение - экспоненциально.
- Алогритм построения матрицы Адамара не является детерминированным.
- Вычилительная мощность данного алгоритма (как соотношение последовательной сложности к сумме входных и выходных данных) равна:
\frac{ (2^{n})^2(2+2n) } {1+(2^{n})^2 } ( то есть \approx 2n если n -\gt +\infty)
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма и его реализации
Исследование масштабируемости параллельной реализации алгоритма построения матрицы Адамара проводилось на суперкомпьютере «Ломоносов»[3]. Объектом исследования стала собственная реализация алгоритма с использованием средств MPI. Наблюдались две переменные - время выполнения алгоритма и количество выполненных операций. Паратметры запуска - это размерность 2^N матрицы Адамара и количество процессоров.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров: [2,32] с шагом 2;
- размер матрицы: степени двойки в диапазоне [2, 16] с шагом 1, то есть, реальная размерность матрицы была в диапазоне [4, 65536].
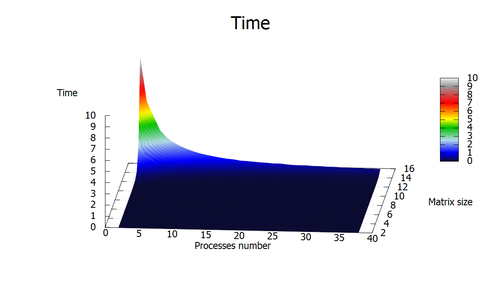
Ниже представлен график времени работы от изменения входных параметров. Как видно, оптимизация программы с ростом числа процессоров идет довольно быстро.
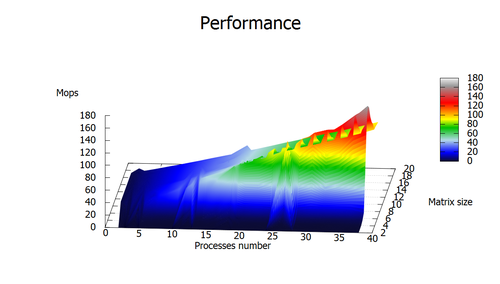
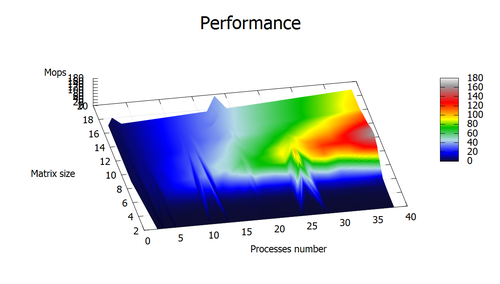
Так как в нашем алгоритме существенно мало операция с плавающей точкой, в качестве альтернативы Flops использовалось значение MIPS . График производительности:
Исследованная параллельная реализация на языке C++
Построим оценки масштабируемости, используя полученные результаты:
- По размерности задачи. При увеличении размера матрицы, производительность также увеличивается. При этом, интересен тот факт, что пиковое значение производительности приходится не на максимальное возможную размерность.
- По числу процессоров. С ростом числа процессоров растет производительность. На малых размерностях матрицы этот рост не очень заметен, но для больших порядков количество процессоров оказывает ключевую роль на производительность.
- По двум направлениям. При одноврменном увеличении числа процессоров и размерности матрицы, производительность растет.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Википедия – свободная энциклопедия [Электронный ресурс]. - https://en.wikipedia.org/wiki/Hadamard_transform. - (дата обращения: 15.10.2016).
- ↑ Кронберг, Ю.И. Ожигов, А.Ю. Чернявский — Алгебраический аппарат квантовой информатики 2
- ↑ http://parallel.ru/cluster