Участница:Ekaterina.ivkina/Метод Якоби вычисления сингулярных чисел и векторов

Эта работа ждет рассмотрения преподавателем
Дата последней правки страницы: 05.12.2016
Авторы этой статьи считают, что задание выполнено.

Метод Якоби вычисления сингулярных чисел и векторов
Последовательный алгоритм
Последовательная сложность	[math]O(n^3)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]2n^2+n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n^2)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Авторы статьи: Ивкина Е.И., Колганова В.В.

Вклад во все разделы равноценный.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Сингулярное разложение было первоначально разработано в дифференциальной геометрии при изучении свойств билинейных форм учеными Эудженио Бельтрами и Камилем Жорданом независимо в 1873 и 1874 годах соответственно. Первое доказательство сингулярного разложения для прямоугольных и комплексных матриц было осуществлено математиками Карлом Эскартом и Гэйлом Янгом в 1936 году.

Сингулярное разложение (Singular Values Decomposition, SVD) является удобным методом при работе с матрицами^[1]. Сингулярное разложение показывает геометрическую структуру матрицы и позволяет наглядно представить имеющиеся данные. Сингулярное разложение используется при решении самых разных задач — от приближения методом наименьших квадратов и решения систем уравнений до сжатия и распознавания изображений. Используются разные свойства сингулярного разложения, например, способность показывать ранг матрицы и приближать матрицы данного ранга. Так как вычисления ранга матрицы — задача, которая встречается очень часто, то сингулярное разложение является довольно популярным методом.

Сингулярным разложением матрицы [math]G (n \times n)[/math] называется разложение вида [math]G = U \Sigma V^T[/math] , где [math]U, V[/math] - унитарные матрицы [math]n \times n[/math], [math]\Sigma[/math] - диагональная матрица [math]n \times n[/math] с вещественными положительными числами на главной диагонали. Столбцы матриц [math]U, V[/math] называются соответственно левыми и правыми сингулярными векторами, а значения на диагонали матрицы [math]\Sigma[/math] - сингулярными значениями матрицы [math]G[/math].

Одним из методов нахождения сингулярного разложения матрицы является метод Якоби. Метод Якоби был предложен Карлом Густавом Якоби в 1846 году и представляет собой итерационный алгоритм вычисления собственных значений и собственных векторов симметричной матрицы. Для вычисления собственных значений необходимо неявно применить метод Якоби к симметричной матрице [math]A = G^T G[/math]. На каждом шаге вычисляется вращение Якоби [math]J[/math], с помощью которого матрица [math]G^TG[/math] неявно пересчитывается в [math]J^TG^TGJ[/math]; вращение выбрано так, чтобы пара внедиагональных элементов из [math]G^TG[/math] обратилась в нули в матрице [math]J^TG^TGJ[/math]. При этом ни [math]G^TG[/math], ни [math]J^TG^TGJ[/math] не вычисляются в явном виде; вместо них вычисляется матрица [math]GJ[/math]. Поэтому алгоритм называется методом односторонних вращений.

1.2 Математическое описание алгоритма

Исходные данные: Матрица [math]G[/math] размера [math](n \times n)[/math] над полем вещественных чисел.

Вычисляемые данные:

[math]\sigma_i[/math] - сингулярные числа матрицы [math]G[/math],
[math]U[/math] - матрица левых сингулярных векторов,
[math]V[/math] - матрица правых сингулярных векторов.

Описание алгоритма:

Шаг 1 Вычисляем матрицу [math]G'[/math] применением одностороннего вращения Якоби к исходной матрице [math]G[/math].

Шаг 2 Повторяем Шаг 1 до тех пор, пока матрица [math]G'^TG'[/math] не станет достаточно близка к диагональной.

Шаг 3 Вычисляем по полученной матрице [math]G'[/math] сингулярные числа [math]\sigma_i[/math] и сингулярные векторы [math]U, V[/math].

Основные формулы метода:

[math]\sigma_i = \parallel G'(:,i)\parallel_2[/math] (2-я норма [math]i[/math]-го столбца в [math]G'[/math]).

[math]U = [u_1, \dots, u_n][/math], где [math] u_i = G'(:,i)/\sigma_i[/math].

[math]V = J[/math], где [math]J[/math] - накопленное произведение вращений Якоби.

Основные формулы процедуры одностороннего вращения Якоби:^[2]

Пусть [math]a_{ij}[/math] - элемент, расположенный в [math]i[/math]-ой строке и [math]j[/math]-ом столбце матрицы [math]G^TG[/math].

[math]\tau = (a_{jj} - a_{kk})/(2 \cdot a_{jk})[/math]

[math]t = sign(\tau)/(|\tau|+\sqrt{1+\tau^2})[/math]

[math]c = 1/\sqrt{1+t^2}[/math], где [math]c = cos\theta[/math]

[math]s = c \cdot t[/math], где [math]s = sin\theta[/math]

[math]G = G \cdot R(j,k,\theta)[/math]

[math]J = J \cdot R(j,k,\theta)[/math]

Здесь [math]R(j,k,\theta)[/math] — матрица вращений Якоби, которая имеет следующий вид:

[math]j[/math] [math]k[/math]

[math] R(j,k,\theta) = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} [/math] [math] \begin{pmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{pmatrix} [/math]

Одностороннее вращение Якоби в координатной плоскости [math]i, j[/math] вычисляется в том случае, если элемент [math]a_{ij}[/math] удовлетворяет условию: [math]|a_{ij}| \geq \varepsilon \sqrt{a_{ii}a_{jj}}[/math].

Проверка близости матрицы к диагональной:

Для проверки близости матрицы [math]A=G'^TG'[/math] к диагональной используется следующее неравенство:

[math]off(A) = \sqrt{\sum_{1\leq j\lt k \leq n} a^2_{jk}} \leq \varepsilon[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро метода Якоби вычисления сингулярных чисел и векторов можно составить из множественных вызовов процедуры одностороннего вращения Якоби One-Sided-Jacobi-Rotation(G,j,k).

Основными операциями процедуры One-Sided-Jacobi-Rotation(G,j,k) являются:

Вычисление элементов [math]a_{jj}, a_{jk}, a_{kk}[/math], где [math]a_{ij} = (G^TG)_{ij}[/math].
Вычисление матрицы вращения Якоби [math]R(j,k,\theta)[/math].
Применение вращения Якоби к матрицам [math]G[/math] и [math]J[/math].

1.4 Макроструктура алгоритма

Алгоритм вычисления сингулярных чисел и векторов Якоби состоит из множественных обращений к процедуре одностороннего вращения Якоби. На каждой итерации цикла происходит вызов процедуры One-Sided-Jacobi-Rotation(G, j, k) для всех [math]j \in [1, n-1][/math] и [math]k \in [j+1, n][/math]. Таким образом, на каждой итерации цикла процедура One-Sided-Jacobi-Rotation(G, j, k) вызывается для всех наддиагональных элементов матрицы [math]G^TG[/math], то есть всего [math]\frac{n(n-1)}{2}[/math] раз. Количество итераций цикла непосредственно зависит от матрицы [math]G[/math]: выход из цикла происходит, когда матрица [math]G^TG[/math] становится достаточно близка к диагональной (описано в разделе "Математическое описание алгоритма").

1.5 Схема реализации последовательного алгоритма

Схему реализации последовательного алгоритма можно описать следующим псевдокодом ^[2]:

repeat
  for  [math]j=1[/math] to [math]n-1[/math]
    for [math]k=j+1[/math] to [math]n[/math]
      One-Sided-Jacobi-Rotation(G, j, k)
    end for
  end for
пока [math]G^TG[/math] не станет достаточно близка к диагональной матрице.
Положить [math]\sigma_i = \parallel G'(:,i)\parallel_2[/math] (2-я норма [math]i[/math]-го столбца в [math]G'[/math]).
Положить [math]U = [u_1, \dots, u_n][/math], где [math] u_i = G'(:,i)/\sigma_i[/math].
Положить [math]V = J[/math], где [math]J[/math] - накопленное произведение вращений Якоби.

Пояснения к псевдокоду:

Пока матрица [math]G^TG[/math] не станет достаточно близка к диагональной, необходимо применять ко всем ее наддиагональным элементам одностороннее вращение Якоби. Обход всех наддиагональных элементов матрицы в последовательной реализации происходит построчно. Когда матрица [math]G^TG[/math] становится достаточно близка к диагональной, происходит выход из цикла и вычисляются сингулярные числа и векторы матрицы [math]G[/math] согласно формулам из псевдокода.

Процедура One-Sided-Jacobi-Rotation(G, j, k):

proc One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
    Вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]\tau = {(a_{jj} - a_{kk})}/{(2a_{jk})}[/math]
        [math]t = {sign(\tau)}/(|\tau| + \sqrt{1 + \tau^2})[/math]
        [math]c = 1/(\sqrt{1 + t^2})[/math]
        [math]s = ct[/math]
        [math]G = GR(j,k,\theta)  [/math], где [math]c=cos\theta, s=sin\theta[/math] 
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

Пояснения к псевдокоду: Для вычисления одностороннего вращения Якоби для одного элемента матрицы необходимо:

Проверить, что выбранный элемент не слишком мал (в противном случае вращение не выполняется).
Вычислить матрицу вращений Якоби для данного элемента.
Применить вращения к матрицам [math]G[/math] и [math]J[/math].

1.6 Последовательная сложность алгоритма

Как описано выше, для вычисления сингулярных чисел и векторов методом Якоби необходимо [math]\frac{n(n-1)}{2}[/math] выполнение процедуры одностороннего вращения Якоби.

Cложность процедуры One-Sided-Jacobi-Rotation(G, j, k):

Вычисление элементов [math]a_{jj}, a_{jk}, a_{kk}[/math], где [math]a_{ij} = (G^TG)_{ij}[/math]. Для вычисления одного элемента [math]a_{ij}[/math] достаточно перемножить только векторы [math]G^T(i,:)[/math] и [math]G(:,j)[/math]. Соответственно потребуется [math]3(2n-1)[/math] операций умножения и сложения.
Вычисление значений [math]\tau, t, c, s[/math] для матрицы вращения Якоби [math]R(j,k,\theta)[/math] требует порядка [math]O(1)[/math] операций.
Вычисление [math]G = GR(j,k,\theta)[/math] и [math]J = JR(j,k,\theta)[/math]. Можно заметить, что [math]G_{il}[/math] при [math]l \ne j,k[/math] при умножении на матрицу [math]R(j,k,\theta)[/math] не изменяются, и необходимо произвести вычисление только столбцов [math]j[/math] и [math]k[/math]. При этом для вычисления одного элемента требуется 3 операции, так как соответствующий столбец матрицы [math]R(j,k,\theta)[/math] имеет только 2 ненулевых элемента. Следовательно, для вычисления [math]G = GR(j,k,\theta)[/math] необходимо выполнить [math]6n[/math] операций и столько же для [math]J = JR(j,k,\theta)[/math].

Таким образом, одно вращение Якоби требует порядка [math]O(n)[/math] операций.

Последовательная сложность алгоритма Якоба равна [math]\frac{n(n-1)}{2} \cdot O(n) = O(n^3)[/math].

1.7 Информационный граф

Опишем граф алгоритма на макро- и микро-уровне.

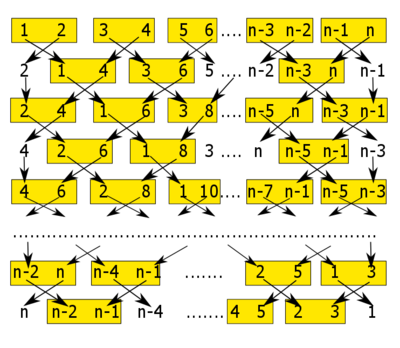
При одном вращении Якоби изменяется всего 2 столбца матрицы [math]G[/math]. Таким образом, есть возможность одновременно выполнять [math]\lceil \frac{n}{2} \rceil[/math] вращений ^[3]. Основной задачей является организация эффективного перебора вершин [math]i,j[/math]. На рисунке 1 изображен один из вариантов такого перебора ^[4]: один элемент со значениями [math]i,j[/math] означает вызов процедуры вращения Якоби One-Sided-Jacobi-Rotation(G, i, j). Столбцы, номера которых выделены белым, во вращении на соответствующем уровне не участвуют.

Рисунок 1. Информационный граф на макроуровне.

Также и процедура одностороннего вращения Якоби содержит ряд функций, которые могут быть вычислены независимо и параллельно:

Вычисление элементов матрицы [math]G^TG[/math]: необходимо вычислить три элемента матрицы [math]G^TG[/math]: [math]a_{jj}, a_{jk}, a_{kk}[/math]. Вычисление одного элемента не зависит от вычисления других, поэтому их можно производить параллельно.

Вычисление элементов матриц [math]GR[/math], [math]JR[/math]: умножение матрицы [math]G[/math] на матрицу вращений Якоби [math]R(j,k,\theta)[/math] изменяет всего два столбца исходной матрицы ([math]j[/math]-й и [math]k[/math]-й). В сумме необходимо вычислить [math]4n[/math] элемента ([math]2n[/math] элементов матрицы [math]G[/math] и [math]2n[/math] элементов матрицы [math]J[/math]), вычисление всех элементов можно производить параллельно.

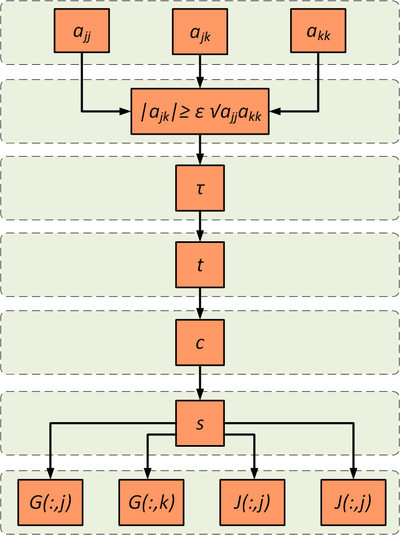
Рисунок 2 иллюстрирует ЯПФ для процедуры одностороннего вращения Якоби. Серая область объединяет вычисления на одном уровне ЯПФ, т.е. вычисления, которые могут быть произведенные параллельно. Каждый выделенный элемент представляет собой набор базовых математических операций типа сложение, умножение, деление и т.д.

Рисунок 2. Информационный граф процедуры одностороннего вращения Якоби.

1.8 Ресурс параллелизма алгоритма

Одним из преимуществ алгоритма Якоби вычисления сингулярных чисел и векторов перед другими алгоритмами является его параллелизм.

Алгоритм Якоби позволяет производить параллельно следующие вычисления (рисунок 2):

Вычисление элементов матрицы [math]G^TG[/math]: необходимо вычислить три элемента матрицы [math]G^TG[/math]: [math]a_{jj}, a_{jk}, a_{kk}[/math]. Вычисление одного элемента не зависит от вычисления других, поэтому их можно производить параллельно.

Сложность операции: вычисления одного элемента требует [math]2n-1[/math] операций, возможно параллельное вычисление трех элементов.

Вычисление элементов матриц [math]GR[/math], [math]JR[/math]: умножение матрицы [math]G[/math] на матрицу вращений Якоби [math]R(j,k\theta)[/math] изменяет всего два столбца исходной матрицы ([math]j[/math]-й и [math]k[/math]-й). В сумме необходимо вычислить [math]4n[/math] элемента ([math]2n[/math] элементов матрицы [math]G[/math] и [math]2n[/math] элементов матрицы [math]J[/math]), вычисление всех элементов можно производить параллельно.

Сложность операции: вычисление одного элемента требует 3 операции, при условии параллельного вычисления всех [math]4n[/math] элементов последовательная сложность данного вычисления будет равна [math]O(1)[/math], при условии параллельного вычисления 4 столбцов последовательная сложность данного вычисления будет равна [math]O(n)[/math].

Вычисление вращений Якоби для всех наддиагональных элементов: (рисунок 1) как описано выше, одно вращение Якоби изменяет всего два столбца исходной матрицы, поэтому параллельно могут быть вычислены вращения для [math]\lceil n/2 \rceil[/math] столбцов матрицы.

Сложность операции: Вычисление вращения Якоби для всех наддиагональных элементов состоит из [math]\frac{n(n-1)}{2}[/math] итераций. При выборе столбцов [math]j[/math] и [math]k[/math] таким образом, чтобы параллельно можно было выполнить [math]\lceil n/2 \rceil[/math] вращений Якоби (вариант выбора итераций описан в разделе Информационный граф), количество последовательных итераций сокращается до [math]n-1 (n)[/math] при четном (нечетном) [math]n[/math] соответсвтенно.

Таким образом, сложность одностороннего вращения Якоби при условии параллельного вычисления сравнима с [math]O(n)[/math].

Высота ярусно-параллельной формы: [math]O(n)\cdot n = O(n^2)[/math]

Ширина ярусно-параллельной формы: [math]O(1)\cdot \frac{n}{2} = O(n)[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: Матрица [math]G[/math] размера [math](n \times n)[/math].

Объём входных данных: [math]n^2[/math]

Выходные данные:

[math]\sigma_i[/math] - сингулярные числа матрицы [math]G[/math] ([math]i = 1,\dots,n[/math]),
[math]U[/math] - матрица размера [math](n \times n)[/math] левых сингулярных векторов,
[math]V[/math] - матрица размера [math](n \times n)[/math] правых сингулярных векторов.

Объём выходных данных: [math]2n^2+n[/math]

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов является линейной (отношение кубической к квадратичной).

Вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – тоже линейна.

Алгоритм Якоби вычисления сингулярных чисел и векторов обладает следующими свойствами ^[2]:

Алгоритм Якоби является самым медленным из всех алгоритмов вычисления сингулярного разложения плотной симметрической матрицы.
Для некоторых видов матриц алгоритм обеспечивает значительно высокую (относительно других методов) точность вычислений:
1. Для матриц [math]G[/math] вида [math]G = DX[/math], где [math]D[/math] - диагональная матрица, а [math]X[/math] - хорошо обусловлена.
2. Для матриц [math]A[/math], где [math]A = LL^T[/math] - разложение Холецкого, и [math]L = DX[/math], где [math]D[/math] - диагональная матрица, а [math]X[/math] - хорошо обусловлена.
3. Для матриц [math]A[/math] вида [math]A = YDX[/math], где [math]D[/math] - диагональная матрица, а [math]X, Y[/math] - хорошо обусловлены, но в остальном произвольные матрицы.
Алгоритм Якоби обладает хорошим ресурсом параллелизма.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на тестовой среде суперкомпьютера "Ломоносов" ^[5] Суперкомпьютерного комплекса Московского университета.

Для анализа использовалась версия библиотеки Intel MKL 11.2.0. Компилятор ICC запускался с параметрами -DMKL_ILP64 -qopenmp -I${MKLROOT}/include -Wl,--start-group ${MKLROOT}/lib/intel64/libmkl_intel_ilp64.a ${MKLROOT}/lib/intel64/libmkl_core.a ${MKLROOT}/lib/intel64/libmkl_intel_thread.a -Wl,--end-group -lpthread -lm -ldl.

Набор и границы значений изменяемых реализации алгоритма:

число процессоров [1 : 16];
размер матрицы [100 : 1300] с шагом 100.

В результате проведённых экспериментов был получен следующий диапазон алгоритма:

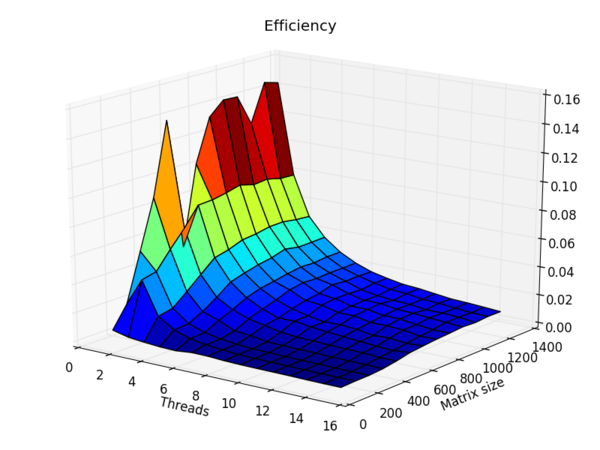
минимальная эффективность реализации 0,102%;
максимальная эффективность реализации 14,82%.

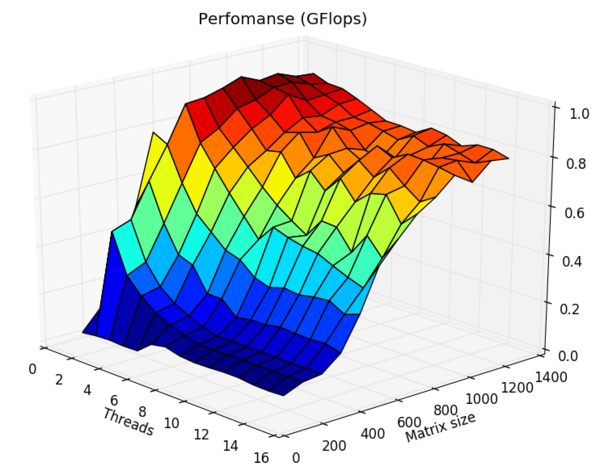
Рисунок 3. Производительность параллельной реализации метода Якоби в зависимости от числа процессоров и размера матрицы..

Рисунок 4. Эффективность параллельной реализации метода Якоби в зависимости от числа процессоров и размера матрицы..

Построим оценки масштабируемости выбранной реализации метода Якоби:

По числу процессов: При увеличении числа процессов эффективность уменьшается. Заметное уменьшение производительности наблюдается при переходе от одного к трем процессам. При дальнейшем увеличении числа процессов (от 4 до 16) эффективность уменьшается незначительно.
По размеру задачи: При увеличении размера задачи эффективность в целом возрастает, однако, возрастание происходит неравномерно, с перепадами.

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Метод Якоби реализован в пакетах: LINPACK ^[6], LAPACK ^[7], SCALAPACK ^[8], Intel MKL ^[9].

3 Литература

↑ |http://www.machinelearning.ru/wiki/index.php?title=Сингулярное разложение
↑ ^2,0 ^2,1 ^2,2 Деммель Д. Вычислительная линейная алгебра. – 2001. - С.261-264.
↑ |Lambers J. CME 335 Spring Quarter 2010-11 Lecture 7 Notes
↑ Zhou B. B., Brent R. P. On parallel implementation of the one-sided Jacobi algorithm for singular value decompositions //Parallel and Distributed Processing, 1995. Proceedings. Euromicro Workshop on. – IEEE, 1995. – С. 401-408.
↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.
↑ Dongarra J. J. et al. LINPACK users' guide. – Siam, 1979.
↑ Anderson E. et al. LAPACK Users' guide. – Siam, 1999. – Т. 9.
↑ Blackford L. S. et al. ScaLAPACK users' guide. – Siam, 1997. – Т. 4.
↑ https://software.intel.com/en-us/articles/intel-math-kernel-library-documentation

[1] |http://www.machinelearning.ru/wiki/index.php?title=Сингулярное разложение

[Dem-2] 2,0 ^2,1 ^2,2 Деммель Д. Вычислительная линейная алгебра. – 2001. - С.261-264.

[3] |Lambers J. CME 335 Spring Quarter 2010-11 Lecture 7 Notes

[4] Zhou B. B., Brent R. P. On parallel implementation of the one-sided Jacobi algorithm for singular value decompositions //Parallel and Distributed Processing, 1995. Proceedings. Euromicro Workshop on. – IEEE, 1995. – С. 401-408.

[Lom-5] Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.

[Lnpck-6] Dongarra J. J. et al. LINPACK users' guide. – Siam, 1979.

[Lpck-7] Anderson E. et al. LAPACK Users' guide. – Siam, 1999. – Т. 9.

[Sclpck-8] Blackford L. S. et al. ScaLAPACK users' guide. – Siam, 1997. – Т. 4.

[MKL-9] ttps://software.intel.com/en-us/articles/intel-math-kernel-library-documentation

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]