Участник:Lvs/Итерационный метод решения системы линейных алгебраических уравнений GMRES
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Evgeny Mortikov и Dan. |
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод минимальных невязок используется для решения систем линейных алгебраических уравнений с заданной точностью приближения. Приближённое решение в методе получается с помощью вектора в подпространстве Крылова. Для нахождения этого вектора используется алгоритм Арнольди, посредством которого матрица СЛАУ приводится к (верхней) хессенберговой форме. На основе этой формы происходит минимизация невязки.
1.2 Математическое описание алгоритма
Дана система линейных алгебраических уравнений Ax = b, где A - квадратная матрица размера n \times n.
Вычисляется последовательность приближённых решений уравнения x_m , которая сходится к точному решению уравнения x^*.
Подпространство Крылова размерности m, порожденное вектором b и матрицей A – линейное пространство K_m(A, v), являющееся линейной оболочкой векторов b, Ab, A^2b, ..., A^{m-1}b.
Приближённое решение считается по формуле x_m = Q_my_m, где Q_m - матрица размера n \times m, составленная из векторов ортонормированного базиса пространства K_m(A, v), y_m \in \mathbb{R}^m.
Итоговым считается решение, минимизирующее норму невязки (||r||_2 = ||b - Ax_m||_2) с заданной точностью.
Для вычисления векторов ортонормированного базиса используется алгоритм Арнольди:
- Значение первого вектора выбирается как q_1 = b / ||b||
- Оставшиеся векторы q_j, j = 2 .. n считаются по такому плану:
- Вычисляется вектор z путём умножения матрицы A на предыдущий вектор q: z = Aq_{j-1}.
- Вычисляются значения h_{ij-1} для всех i = 1 .. j - 1 как скалярное произведение вектора z на вектор q_i: h_{ij-1} = (z, q_i). После каждого такого вычисления значение вектора z понижается на h_{ij-1} q_i: z = z - h_{ij-1} q_i
- Затем вычисляется значение h_{jj-1} как норма вектора z: h_{jj-1} = ||z||. Алгоритм останавливается, если эта норма равна 0
- Если полученное значение нормы не равно 0, то q_j = z /||z|| (что эквивалентно q_j = z /h_{jj-1}
Сложность алгоритма O(n^2).
Получаемые в процессе работы алгоритма векторы q_1, q_2, ..., q_m образуют искомый ортонормированный базис Крыловского пространства K_m(A, b).
Значения h_{i,j} образуют верхнюю матрицу Хессенберга (обозначим как H_m, размерность m+1 \times m).
H_m = \begin{bmatrix}h_{11} & h_{12} & h_{13} &... & h_{1m-1} & h_{1m} \\ h_{21} & h_{22} & h_{23} & ... & h_{2m-1} & h_{2m} \\ 0 & h_{32} & h_{33} &...& h_{3m-1} & h_{3m} \\ ... & ... & ... & ... & ... & ... \\ 0 & 0 & 0 & ... & h_{m m-1} & h_{mm} \\0 & 0 & 0 & ... & 0 & h_{m+1 m}\end{bmatrix}.
Вектор невязки задан уравнением r_m = H_my_m - ||b - Ax_0||e_1, где x_0 - вектор начального приближения. Минимизация второй нормы вектора невязки представляет из себя решение линейной задачи минимальных квадратов размера n.
Приближённое решение вычисляется по формуле x_m = Q_my_m после нахождения соответствующего значения минимизирующего вторую невязку вектора. Сложность вычислений O(nm)
1.3 Вычислительное ядро алгоритма
Самая трудоёмкая и самая часто вызываемая операция в алгоритме - умножение матрицы на вектор. В первую очередь это связано с вычислением матрицы Хессенберга и ортонормированного базиса подпространства Крылова. Число умножений матрицы на вектор: n-1 в алгоритме Арнольди, K в выбранном алгоритме решения задачи минимальных квадратов и 1 в подсчёте результата. Также в алгоритм входят n*(n-1) / 2 операций скалярного произведения.
1.4 Макроструктура алгоритма
- Алгоритм Арнольди
- Решение линейной задачи минимальных квадратов
- Вычисление решения
1.5 Схема реализации последовательного алгоритма
Вычислить ортонормированный базис размера m
Вычислить минимальное приближение (минимальную норму вектора невязки)
if (приближение < заданная точность)
Вычислить результат
return;
else
Повторить для m = m+11.6 Последовательная сложность алгоритма
Сложность вычислений собственных векторов на каждом шаге - O(n^2).
Сложность решения задачи минимальных квадратов O(m^2), но при последовательном выполнении алгоритма можно понизить сложность до O(m) путём использования подсчитанных на прошлых итерациях значений.
Сложность вычисления решения O(nm), поэтому его целесообразно вычислять только в конце.
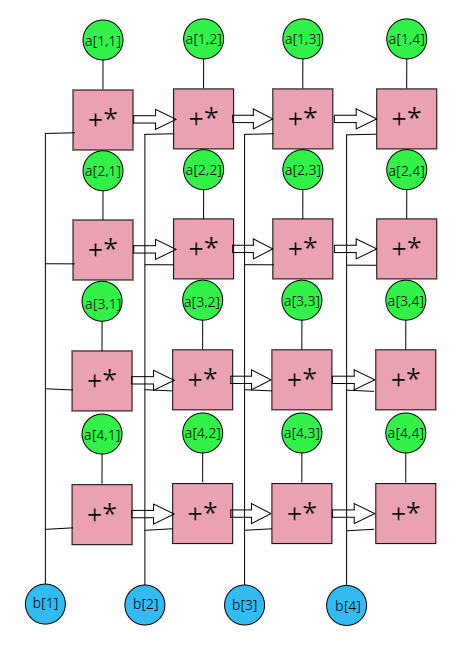
1.7 Информационный граф
Основной ресурс параллелизма - умножение матрицы на вектор, поскольку является самым ресурсоёмким, но при этом умножать отдельные строки матрицы можно независимо друг от друга. Для этой операции информационный граф представлен на рисунке.
1.8 Ресурс параллелизма алгоритма
- Параллельное умножение матрицы на вектор выполняется в n ярусов умножений и сложений.
- Операция вычисления скалярного произведения
- Шаги алгоритма Арнольди выполняются строго последовательно, однако последующее нахождение невязки можно выполнять параллельно с запуском следующего шага алгоритма.
- Сложность решения задачи минимальных квадратов зависит от используемого алгоритма. В отличие от последовательного метода данные, полученные на прошлых шагах здесь использовать нельзя.
- Вычисление результата выполняется один раз, его можно выполнить параллельно в n ярусов умножений и сложений.
1.9 Входные и выходные данные алгоритма
Входные данные: Матрица A, вектор b, точность t. Объём: n^2 + n + 1
Выходные данные: Вектор x_m. Объём: n
1.10 Свойства алгоритма
Теоретически на каждой итерации алгоритма сложность вычислений составляет n + X операций умножения, где X - сложность алгоритма для решения задачи минимальных квадратов. Таким образом в худшем случае сложность будет примерно равна n^2 + X*n + n операций умножения.
Несмотря на то, что в теории итерации алгоритма можно выполнять параллельно после выполнения алгоритма Арнольди, на практике необходимая точность может быть достигнута раньше чем на n-й итерации, что потребует какого-нибудь способа прервать последующие итерации. Для избегания лишних вычислений возможно оптимально выполнять итерации алгоритма последовательно, вычисляя параллельно только векторно-матричные произведения.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
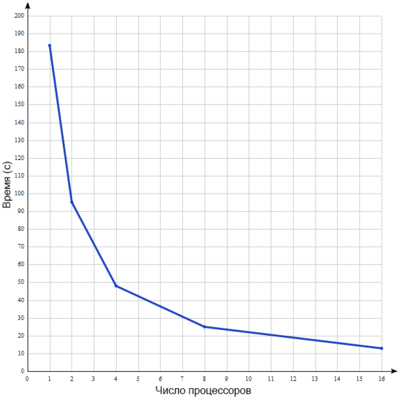
Для исследования масштабируемости алгоритма была использована параллельная реализация, найденная на просторах GitHub[1]. Эта реализация использует многопроцессорное выполнение с общей памятью и вычисляет параллельно скалярное произведение и умножение матрицы на вектор. Программа была запущена на суперкомпьютере BlueGene на разреженной матрице размера 90448х90448 с 1921955 ненулевыми элементами, расположенными около главной диагонали. Параметрами запуска являются 100 итераций алгоритма и 10 перезапусков алгоритм (повторный запуск алгоритма с использованием решения, полученного на предыдущем запуске, в качестве начального приближения). График зависимости времени выполнения от числа процессоров представлен на рисунке 2.
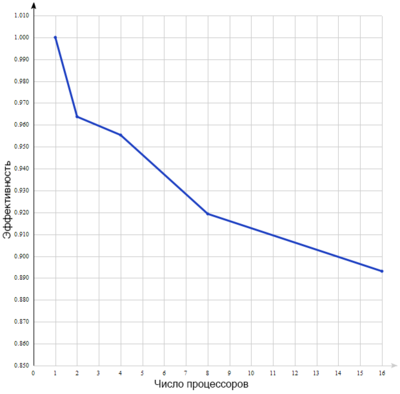
График эффективности для полученного времени выполнения указан на рисунке 3.
Параметры компиляции:
mpixlc_r -qsmp=omp -O3
Параметры запуска:
gmres mat.mtx void 100 0 10
Надо заметить, что для этой матрицы на таком числе итераций решения с заданной точностью найдено не было. Она была выбрана с целью показать масштабируемость алгоритма. На матрицах более малого размера решение находится быстро.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Реализации алгоритма GMRES присутствуют во многих программных продуктах как части стандартных библиотек, например Matlab или DEFORM3D. Также существую отдельные библиотеки, например MGMRES для языка С++.
3 Литература
[1] Тыртышников Е. Е. Методы численного анализа — М., Академия, 2007.
[2] М. Дана, А. Г. Зыков, Х. Д. Икрамов Метод минимальных невязок для специального класса линейных систем с нормальными матрицами коэффициентов - Ж. вычисл. матем. и матем. физ., 2005, том 45, номер 11
- ↑ Parallel GMRES Algorithm for Solving Giant Sparse System of Linear Equations https://github.com/arrgasm/paraGMRES/