Участник:Nikmedoed/Нечеткий алгоритм С-средних (Fuzzy C-means)

Эта работа прошла предварительную проверку Дата последней правки страницы: 17.12.2016 Данная работа соответствует формальным критериям. Проверено Illusive mike.

Нечеткий алгоритм С-средних (Fuzzy C-means)
Последовательный алгоритм
Последовательная сложность	[math]O(c^2 MI + cMnI), (I[/math] - число итераций, [math]c[/math] - количество кластеров, [math]M[/math] - число точек, [math]n[/math] - размерность точек (свойств на объект)[math])[/math]
Объём входных данных	[math]Mn[/math]
Объём выходных данных	[math]cM[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] O(c^2 I + cnI)[/math]
Ширина ярусно-параллельной формы	[math]O( M )[/math]

Авторы: Н.А. Муромцев - перенос в вики, раздел 2, картинки, М.С. Дворецкий - раздел 1

Нечеткий алгоритм С-средних (Fuzzy C-means) - позволяет получить нечёткую кластеризацию больших наборов числовых данных, что позволяет корректно определять объекты на границах кластеров. Однако, выполнение данного алгоритма требует серьёзных вычислительных ресурсов, а также изначального задания количества кластеров. Кроме того, может возникнуть неоднозначность с объектами, удалёнными от центров всех кластеров.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм кластеризации Fuzzy C-Means (FCM) был предложен Дж. Данном в 1973 году и доработан Дж. Бездеком в 1981 году . В отличие от большинства существующих алгоритмов кластеризации, данный алгоритм является нечётким – каждый из объектов не входит однозначно в какой-либо кластер, а принадлежит всем кластерам с различными степенями принадлежности. Это даёт преимущества в качестве разбиения в случаях, когда кластеры находятся близко друг к другу, и большое число точек находится на их границах. Однако ценой такой нечёткости служат большие вычислительные затраты, чем у таких чётких алгоритмов, как Hard C-Means и K-Means, при сохранении таких их недостатков, как априорное определение числа кластеров и отсутствие гарантии глобальной оптимальности результата.

1.2 Математическое описание алгоритма

Исходные данные: массив объектов [math]{X_k}\in{\R^n}, k=\overline{1,M}[/math], число кластеров c, экспоненциальный вес [math]m\in{[1,\infty)}[/math], параметр останова [math]\varepsilon\gt 0[/math].

Вычисляемые данные: матрица разбиения [math]F[/math] размера [math]M\times c[/math] (элементы [math]\mu_{ki}\in[0,1][/math], [math]\sum^{c}_{i=1} {\mu_{ki}} = 1[/math]), центры кластеров [math]V_i[/math], расстояния [math]D_{ki}[/math] между объектами и центрами кластеров.

Формулы метода (вычисляются последовательно на каждой итерации):

1. Уточнение центров кластеров по степеням принадлежности

[math] \begin{align} &V_i=\frac{\sum^{M}_{k=1} {\mu^m_{ki} * X_k}}{\sum^{M}_{k=1} {\mu^m_{ki}}},i=\overline{1,c} \end{align} [/math]

2. Расчёт расстояний между новыми центрами кластеров и точками данных

[math] \begin{align} &D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c} \end{align} [/math]

3. Пересчёт степеней принадлежности объектов кластерам

[math] \begin{align} &\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} \left ( {\frac{D_{ki}}{D_{kj}}} \right ) }^{{2}/{m-1}} },k=\overline{1,M},i=\overline{1,c}\\ \end{align} [/math]

На каждой итерации алгоритма происходит уточнение элементов матрицы [math]F[/math]. Выходом алгоритма служит матрица [math]F[/math], к которой алгоритм сходится. Факт того, что алгоритм сошёлся, устанавливается проверкой вида [math]\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} \lt \varepsilon[/math] либо [math]\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} \lt \varepsilon[/math], где [math]\mu_{ki}^* (V_i^*)[/math] – значение [math]\mu_{ki}(V_i)[/math], вычисленное на предыдущей итерации.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма Fuzzy C-Means составляют шаги вычисления центров кластеров, расстояний между ними и точками данных и в особенности пересчёта матрицы степеней принадлежности точек данных.

При реализации алгоритма некоторые повторяющиеся вычисления могут быть устранены. Так, для шага вычисления центров кластеров величины [math]\mu_{ki}^m[/math] могут вычисляться однократно и умножаться на [math]X_k[/math] при включении в сумму, записанную в числителе. Для шага вычисления расстояний между центрами кластеров и точками, операция взятия квадратного корня не является обязательной, так как в дальнейшем на шаге вычисления степеней принадлежности можно непосредственно использовать квадраты этих расстояний, и сумма в знаменателе будет приобретать вид:

[math]\sum^{c}_{j=1} {\left ( \frac{D_{ki} ^ {2}}{D_{kj} ^ {2}} \right )}^{{1}/{m-1}}[/math]

1.4 Макроструктура алгоритма

Алгоритм включает в себя три основных этапа – вычисление центров кластеров, вычисление расстояний между центрами кластеров и точками данных (включающее в себя макрооперации вычитания векторов и вычисления их норм, как правило в Евклидовом пространстве) и пересчёт матрицы принадлежности.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения алгоритма следующая:

Инициализация происходит случайным заполнением матрицы принадлежности [math]F[/math] с соблюдением условия нормировки [math]\sum_{i=1}^c {\mu_{ki} =1}[/math] и переходом к шагу 1, либо случайным определением центров кластеров [math]V_i[/math] и переходом к шагу 2.

Далее осуществляются итерации следующего вида:

1. [math]V_i=\frac{\sum_{k=1}^{M} {\mu_{ki}^m * X_k}}{\sum_{k=1}^{M} {\mu_{ki}^m} },i=\overline{1,c}[/math]
2. [math]D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}[/math]
3. [math]\mu_{ki}=\frac{1}{{ \sum^{c}_{j=1} {\left ( \frac{D_{ki}}{D_{kj}} \right )} }^{{2}/{m-1}} },k=\overline{1,M},i=\overline{1,c}[/math]

В конце каждой итерации проверяется условие останова вида [math]\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} \lt \varepsilon[/math], либо [math]\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} \lt \varepsilon[/math], где [math]\mu_{ki}^* (V_i^*)[/math] – значение [math]\mu_{ki}(V_i)[/math], вычисленное на предыдущей итерации. Если условие не выполнено, осуществляется переход к шагу 1.

1.6 Последовательная сложность алгоритма

При кластеризации [math]M[/math] объектов данных, представленных точками в [math]\R^n[/math], на [math]c[/math] кластеров, алгоритм Fuzzy C-Means в последовательном варианте имеет вычислительную сложность – [math]O(c^2 MI+cMnI)[/math], где [math]I[/math] – число итераций. Если считать размерность данных [math]n[/math] малой, то эта сложность сводится к [math]O(c^2 MI)[/math]. Основной частью алгоритма в этом случае является пересчёт матрицы принадлежностей, требующий вычисления [math]cM[/math] сумм из [math]c[/math] слагаемых на каждой итерации.

1.7 Информационный граф

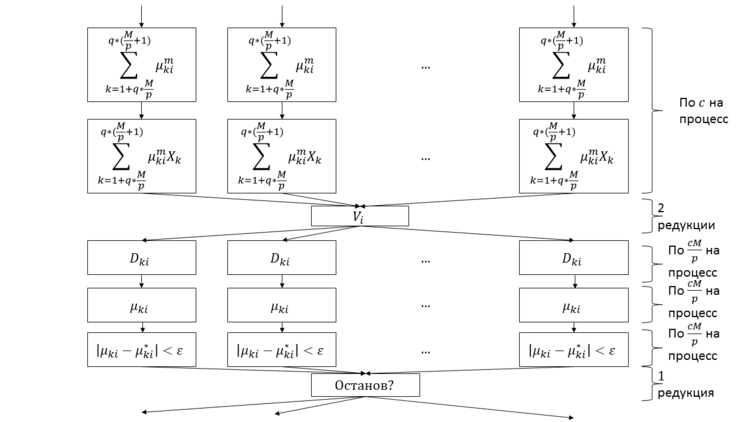
Приведём граф единичной итерации алгоритма в параллельном оптимизированном варианте (метод распараллеливания взят в ):

Каждая вершина данного графа соответствует операциям из алгоритма, указанным при помощи указанных формул. Каждый из p столбцов соответствует работе одного из процессов. Пометки справа указывают число повторений каждого узла в ходе одной итерации.

Раздел 1.8 уточняет, соответствуют ли эти повторения однотипным ярусам или точкам данных, вычисления для которых можно распараллелить и далее.

Каждый процесс обладает следующими данными:

• координатами точек данных [math]X_k[/math], [math]k=\overline{1+rnk* \frac{M}{p},rnk*(\frac{M}{p}+1)}[/math], где [math]rnk[/math] – номер процесса,
• значениями [math]\mu_{ki}[/math] степени принадлежности для своих точек ([math]k=\overline{1+rnk* \frac{M}{p},rnk*(\frac{M}{p} +1)}, i=\overline{1,c}[/math]),
• координатами центров кластеров [math]V_i[/math], [math]i=\overline{1,c}[/math].

Суммы [math]\sum_{k=1+rnk*\frac{M}{p}}^{rnk * ( \frac{M}{p} +1 )} {\mu_{ki}^m}[/math] и [math]\sum_{k=1+rnk*\frac{M}{p}}^{rnk * ( \frac{M}{p} +1 )} {\mu_{ki}^m X_k}[/math] вычисляются одновременно, поэтому значения [math]\mu_{ki}^m[/math] вычисляются по одному разу за итерацию. Таким образом, второй ярус операций на рисунке на деле не содержит операций возведения в степень. За счёт линейности большинства выражений относительно данных по точкам, процессы взаимодействуют только при редукции сумм, составляющих [math]V_i[/math]. Всё остальное время каждый процессор работает только со своими [math]\frac{M}{p}[/math] точками. Это обеспечивает применимость алгоритма для больших [math]M[/math].

1.8 Ресурс параллелизма алгоритма

При распараллеливании по точкам исходных данных и условии останову по малому изменению степеней принадлежности выполнение одной итерации алгоритма FCM может быть разделено на следующие ярусы:

• [math]c[/math] ярусов нахождения частичных сумм знаменателя (по [math]\frac{M}{p}-1[/math] сложений, [math]\frac{M}{p}[/math] операций возведения в степень на процесс),
• [math]c[/math] ярусов нахождения частичных сумм числителя (по [math]\frac{M}{p} -1[/math] сложений, [math]\frac{M}{p}[/math] умножений на процесс),
• [math]2[/math] редукции сумм и передач значений [math]V_i[/math] процессам (получение [math]c(n+1)[/math] значений, [math]cn[/math] делений),
• [math]c[/math] ярусов вычисления расстояний до центров (по [math]n-1[/math] сложений, [math]n[/math] вычитаний, [math]n[/math] умножений), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
• [math]c[/math] ярусов вычисления степеней принадлежности точек (по [math]c+1[/math] делений, c возведений в степень, [math]c-1[/math] сложений), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
• до [math]c[/math] ярусов проверки условий останова (по [math]1[/math] вычитанию, [math]1[/math] сравнению), каждый процесс получает [math]\frac{M}{p}[/math] точек на обработку,
• [math]1[/math] редукция для обмена статусом завершения.

Таким образом, при распараллеливании по точкам исходных данных при условии наличия в каждом узле достаточного объёма памяти для хранения всего массива координат центров кластеров высота и ширина ЯПФ алгоритма FCM равны соответственно [math]O(c^2 I+cnI)[/math] и [math]O(M)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: массив векторов [math]X_i[/math], число кластеров [math]c[/math], экспоненциальный вес [math]m\in{[1,\infty)}[/math], параметр останова [math]\varepsilon\gt 0[/math].

Объём входных данных: [math]Mn[/math] для входных векторов, 3 вспомогательных параметра.

Выходные данные: матрица принадлежности [math]F[/math] (элементы [math]\mu_{ki}\in[0,1][/math]). Условие нормировки: [math]\sum^{c}_{i=1} {\mu_{ki}} = 1[/math].

Объём выходных данных: [math]cM[/math].

1.10 Свойства алгоритма

В случае неограниченного распараллеливания по точкам данных (1 процесс на точку), отношение последовательной сложности алгоритма к параллельной пропорционально [math]M[/math].

Параметр [math]m[/math] задаёт степень «размытости» кластеров. В отсутствие априорных данных его обычно берут равным 2. В предельном случае сведения параметра [math]m[/math] к значению 1, кластеры становятся чёткими и алгоритм вырождается в алгоритм кластеризации K-Means.

Алгоритм недетерминирован, начальное положение кластеров задаётся случайно либо явно, либо опосредованно (через матрицу принадлежности). Алгоритм сходится к локальному экстремуму и, таким образом, не гарантирует оптимальный результат при случайном выборе начальных значений.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

График зависимости времени выполнения итерации параллельного нечеткого алгоритма С-средних (Fuzzy C-means) от количества процессоров и количества кластеризуемых вершин

График эффективности распараллеливания нечеткого алгоритма С-средних (Fuzzy C-means) в зависимости от количества процессоров и количества кластеризуемых вершин.

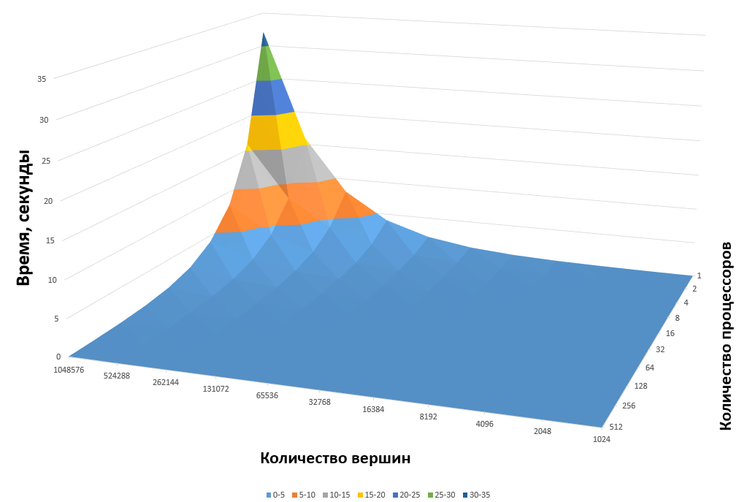
Исследование проведено на суперкомпьютере IBM Blue Gene/P. Для исследования была использована последовательная реализация алгоритма и реализован её параллельный вариант. Алгоритм обладает плохо исследованной сходимостью, но объем вычислений на итерации не зависит от значений данных, поэтому данное исследование масштабируемости было произведено для единичной итерации.

Для упрощения экспериментов было решено использовать количество вершин для кластеризации и количество процессов равное степени двойки, поэтому для каждого эксперимента были выбраны значения:

• [math]2^v, v=\overline{0,9}[/math], для количества процессоров;
• [math]2^w, w=\overline{10,20}[/math], для количества кластеризуемых вершин.

Для одного набора значений проводилось 4 эксперимента и результаты усреднялись. При повторных запусках экспериментов значения выходили те же самые.

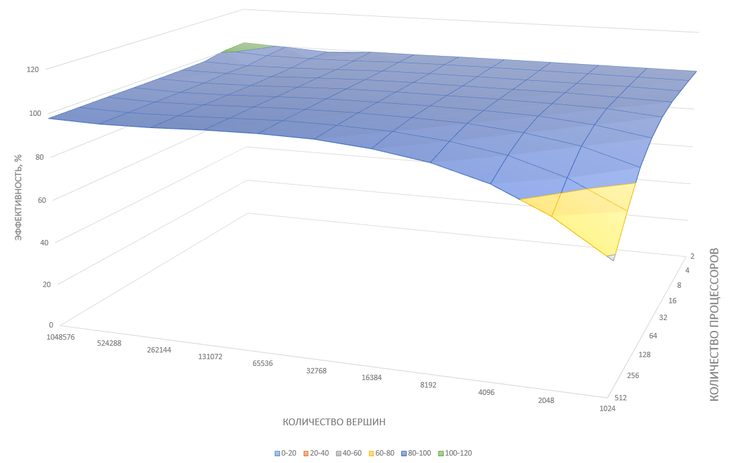
Полученные результаты говорят о хорошей масштабируемости реализации алгоритма. Для большинства экспериментов эффективность распараллеливания находится в пределах 100±3%. Высокая эффективность обуславливается тем, что данные равномерно распределены по процессорам и на каждой итерации требуется глобальная редукция всего [math]2c+1[/math] значений ([math]c[/math] значений числителей центроид кластеров, [math]c[/math] значений знаменателей центроид кластеров и одно значение признака останова). Таким образом вычисления занимают значительно больше времени, чем взаимодействия между процессами, которые практически не приводят к простоям из-за хорошей балансировки. Спад эффективности при малом числе вершин и большом числе процессоров обуславливается тем, что с уменьшением числа вершин, обрабатываемых каждым процессором, растёт доля времени обмена данных между процессорами, не зависящего от числа вершин, как показано выше.

2.7 Существующие реализации алгоритма

• пакет MATLAB
• Реализация алгоритма на POSTGRESQL