Уровень алгоритма

Участник:Gkhazeeva/Нечеткий алгоритм C средних

Материал из Алговики
Версия от 23:58, 19 декабря 2016; Gkhazeeva (обсуждение | вклад)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к навигации Перейти к поиску
Symbol wait.svgЭта работа прошла предварительную проверку
Дата последней правки страницы: 19.12.2016
Данная работа соответствует формальным критериям.
Проверено Coctic.



Нечеткий алгоритм C средних
Последовательный алгоритм
Последовательная сложность [math]O(c^2 Mn_{iter} + cMdn_{iter})[/math], [math]n_{iter} [/math] - количество итераций
Объём входных данных [math]M*d[/math], [количество наблюдений * размерность]
Объём выходных данных [math]M*c[/math], [количество наблюдений * количество кластеров]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(cdn_{iter} + c^2n_{iter})[/math]
Ширина ярусно-параллельной формы [math]O (M) [/math]


Авторы : Гелана Хазеева (1.3; 1.5; 1.6; 1.7; 2.4; 2.7), Павел Юшин (1.1; 1.2; 1.4; 1.8; 1.9; 1.10)

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация - это объединение объектов в группы (кластеры) на основе схожести признаков для объектов одной группы и отличий между группами. Нечеткий алгоритм C Средних (Fuzzy C-means, FCM) - алгоритм кластеризации, позволяющий объектам принадлежать с различной степенью нескольким кластерам одновременно. Впервые алгоритм был предложен J.C. Dunn в 1973 [1]. Нечеткое разбиение позволяет просто решить проблему определения кластера для объектов, расположенных на границе - им назначают степени принадлежностей равные 0.5.

Входные данные алгоритма: набор векторов, которые следует кластеризовать.

Параметры алгоритма: [math]c[/math] - количество кластеров;[math]m \gt = 1[/math] - параметр, определяющий нечеткость кластеров ( при [math]m = 1[/math] разбиение является четким, с увеличением параметра [math]m[/math] растет степень "размазанности" объектов по кластерам); [math]\varepsilon[/math] - параметр останова алгоритма.

Выходные данные: матрица вероятностей принадлежности векторов кластерам.

Краткое описание алгоритма:

  • Задать параметры алгоритма.
  • Сгенерировать случайную матрицу принадлежностей векторов кластерам (матрицу нечеткого разбиения).
  • Повторить следующие шаги до тех пор, пока расстояние между матрицами нечеткого разбиения на этом и предыдущем шаге алгоритма не будет отличаться менее, чем на параметр останова.
    • Рассчитать центры кластеров.
    • Рассчитать расстояние между объектами и центрами кластеров.
    • Пересчитать элементы матрицы нечеткого разбиения.

1.2 Математическое описание алгоритма [2]

Пусть [math] W = w_{ij} \in[0,1],\; i = 1, ..., M, \; j = 1, ..., c[/math] - матрица разбиения, где [math]w_{i,j}[/math] - степень принадлежности объекта [math]i[/math] к кластеру [math]j[/math]; [math]c[/math] - количество кластеров, [math]M[/math] - количество векторов, [math]X_i[/math] - набор входных векторов размерности [math]d[/math].

В качестве нормы предлагается максимум-норма: [math]||W|| = \max_{i,j} |w_{i,j}|[/math]

При этом элементы матрицы должны удовлетворять условиям:

  • [math]\sum_{j = 1}^c w_{ij} = 1, i = 1, ..., M[/math]                [math](1)[/math]
  • [math]0 \lt \sum_{i = 1}^M w_{ij} \lt M, j = 1, ..., c[/math]       [math](2)[/math]

Тогда алгоритм принимает следующий вид:

1) Задаем параметры алгоритма: [math]c[/math] - количество кластеров; [math]m \gt = 1[/math] - экспоненциальный вес, определяющий нечеткость кластеров; [math]\varepsilon \gt 0[/math] - параметр останова алгоритма.

2) Генерируем случайным образом матрицу нечеткого разбиения с учетом условий [math](1)[/math] и [math](2)[/math]

3) Рассчитываем центроиды (центры кластеров): [math]V_j = {{\sum_{i=1}^M w_{ij}^m * X_i} \over {\sum_{i=1}^M w_{ij}^m}}, j = 1, ..., c[/math]

4) Рассчитываем расстояния между объектами [math]X[/math] и центроидами:

[math]D_{ij} = {||X_i - V_j||}, i = 1,...,M; j = 1,...,c [/math]

5) Пересчет элементов матрицы разбиения:

при [math]D_{ij} \gt 0[/math] : [math]w_{ij} = {{1}\over {{ (\sum_{k=1}^c {{D_{ij}}\over{D_{ik}}} ) }^{2/(m-1)}}}, j = 1,...,c[/math]

при [math]D_{ij} =0[/math] : [math]w_{ij} = \delta_{ij}, j = 1,...,c[/math], где [math]\delta_{ij}[/math] - символ Кронекера

6) Если [math]|| F - F^{*} || \lt \varepsilon [/math], где [math]F^{*}[/math] - матрица нечеткого разбиения предыдущей итерации, то идем далее, иначе возвращаемся на пункт 3.

7) Конец.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма являются следующие пункты:

  • Поиск [math]V_j[/math] - расчет центроидов (пункт 3 алгоритма)
  • Нахождение [math]D_{ij}[/math] - расстояний между объектами (пункт 4 алгоритма)
  • Пересчет [math]w_{ij}[/math] - элементов матрицы разбиения (пункт 5 алгоритма)

1.4 Макроструктура алгоритма

Основные шаги при реализации алгоритма

  • Генерация случайной матрицы размера [math]M*c[/math], проверка условий
  • Расчет центроидов – по сути, скалярное произведение с нормировкой
  • Расчет расстояний – в общепринятом случае является скалярным произведением
  • Пересчет матрицы – по сути, скалярное произведение
  • Проверка условий останова – вычисление нормы

1.5 Схема реализации последовательного алгоритма

   float ** FuzzyCMeans (float** X, c, m, eps){
       n = X.size();
       r = X[0].size();
       centers = generateZeroFill(c, r)
       Wprev = genetateRandFill(n, c);
       W = Wprev;
       while (true){
           // обновляем центры кластеров 
           for (int i=0; i<c; i++){
               float * num = new float []();
               float den = 0;
               for (int j=0; j<n; j++){
                   num += pow(W[j][i], m) * X[j];
                   den+=pow(W[j][i], m);
               }
               centers[i] = num / den;
           }
           //обновляем вероятности W и считаем расстояние между матрицами W и Wprev
           float max_diff = 0;
           for (int i=0; i<n; i++)
               for (int j=0; j<c; j++){
                   total = 0;
                   for (int m=0; m<с; m++)
                       total += pow(distance(X[i], centers[j]) / distance(X[i], centers[m]), 2/(m-1));
                   W[i][j] = 1/total;
                   max_diff = max(abs(Wprev[i][j]-W[i][j]), max_diff);
                   Wprev[i][j] = W[i][j];
              }               
          if (max_diff < eps):                
               break;
       }
       return W;
   }

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма состоит из сложности каждой итерации умноженной на их количество [math] n_{iter} [/math]. Так как число итераций заранее неизвестно и зависит от входных параметров, рассмотрим сложность на каждой итерации. Наибольшую сложность представляет собой пересчет матрицы, сложность которого [math]O(c^2 M)[/math] (по сравнению со сложностью [math]O(cMd)[/math] расчета расстояний, вычисления центроидов и проверки условия останова). Итого общая сложность алгоритма [math]O(c^2 Mn_{iter} + cMdn_{iter})[/math]. Так как обычно [math] n \gt \gt c [/math], то в этом случае сложность [math]O(c^2 Mn_{iter} )[/math].

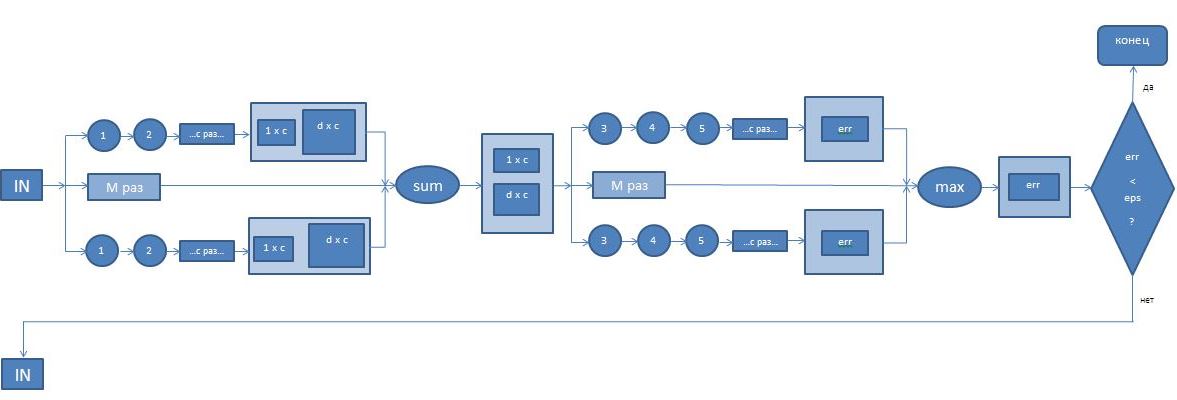
1.7 Информационный граф

Информационный граф представлен на рисунке ниже.

Первый ярус состоит из [math]n_{p}[/math] параллельных процессов, между которыми равномерно распределены [math]M[/math] операций 1, 2, совершаемых в цикле [math]c[/math] раз для каждого кластера.

Операция 1: [math]w_{ij}^m[/math], где [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

Операция 2: [math]w_{ij}^m*X_i[/math]

Здесь [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

На выходе из каждой ветки получаем вектор размера [math]1[/math] x [math]c[/math] и матрицу размера [math]d[/math] x [math]c[/math]. Далее совершаем поэлементное сложение векторов и матриц соответственно, а затем делим каждый столбец в матрице на соответствующий элемент в векторе.

Второй ярус состоит из [math]n_{p}[/math] параллельных процессов, между которыми равномерно распределены [math]M[/math] операций 3, 4, 5 также совершаемых в цикле [math]c[/math] раз.

Операция 3: обновление значения [math]w_{ij}[/math] по указанной в разделе 1.2 в пункте 5 формуле.

Операция 4: [math]maximum = max(|w_{ij} - w_{ij}^{prev}|, maximum)[/math].

Операция 5: [math]w_{ij}^{prev} = w_{ij}[/math].

Здесь [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

На выходе из каждой ветки получаем число [math]maximum[/math]. Далее находим максимальное значение из полученных величин для каждой ветки. Затем проверяем условие останова алгоритма.

Scheme3.JPG

1.8 Ресурс параллелизма алгоритма

На первом ярусе происходит [math] O(cdn_{iter}) [/math] операций, на втором - [math] O(c^2n_{iter}) [/math], итого высота ЯПФ алгоритма [math] O(cdn_{iter} + c^2n_{iter}) [/math]. Ширина ярусно-параллельной формы алгоритма равна [math] O(M) [/math]. Иерархическая структура параллелизма подробно описана в п.1.7.

В алгоритме не возникает скошенного параллелизма.

1.9 Входные и выходные данные алгоритма

  • Входные данные алгоритма: набор векторов [math]x_i[/math] размерности [math]d[/math], где [math]i = 1,...,M[/math]; [math]M[/math] - количество векторов.
  • Объем входных данных: [math]M*d[/math] , [количество наблюдений * размерность].
  • Выходные данные алгоритма: матрица вероятностей принадлежности векторов кластерам [math]M[/math] на [math]c[/math].
  • Объем выходных данных: [math]M*c[/math] , [количество наблюдений * количество кластеров].

1.10 Свойства алгоритма

  • Соотношение последовательной и параллельной сложности: [math]M[/math]
  • Вычислительная мощность: [math]{dc^2n_{iter} } \over {c+d}[/math].
  • Устойчивость: алгоритм не является устойчивым, поэтому существует много исследований о том, как первоначально выбрать параметры кластеризации.
  • Сбалансированность: в данном алгоритме операция умножения доминирует над операцией сложения. Операции между параллельными ветвями сбалансированы.
  • Детерминированность: алгоритм не является детерминированным, так как матрица нечеткого разбиение генерируется произвольно.
  • Степень исхода вершины информационного графа (для одной итерации): 2. Если выходные данные пошли на следующую итерацию: 3.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проведём исследование масштабируемости параллельной реализации нечеткого алгоритма С-средних. Исследование проводилось на суперкомпьютере "Ломоносов"[3] Суперкомпьютерного комплекса Московского университета. Была исследована собственная параллельная реализация алгоритма, написанная на языке C++ с использованием стандарта MPI. Сборка программы производилась при помощи компилятора компании Intel версии 13.1.0 с использованием библиотеки intelMPI версии 4.1.0 . Расчеты проводились в разделе test на узлах со следующими характеристиками: количество GPU - 0, количество ядер - 8 ядер архитектуры x86, количество памяти - 12 Гб.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

  • число процессоров [1 : 128];
  • размер матрицы [10000 : 80000].

В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

  • минимальная эффективность реализации 0,33%;
  • максимальная эффективность реализации 9,4%.


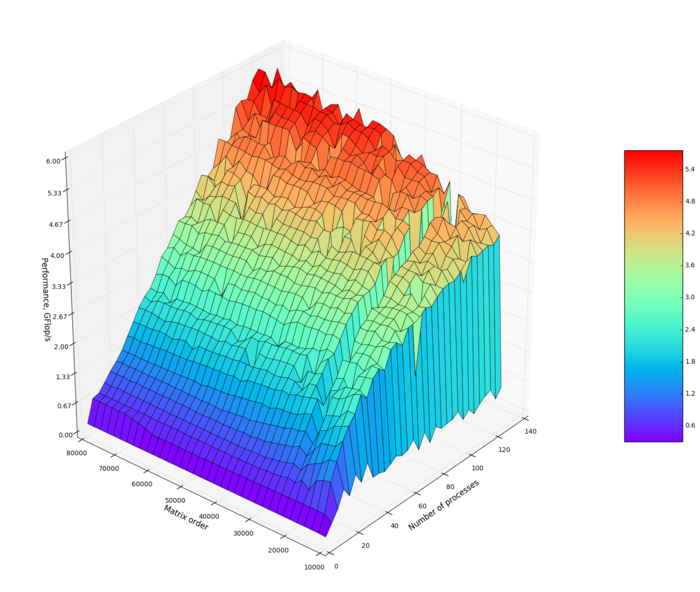
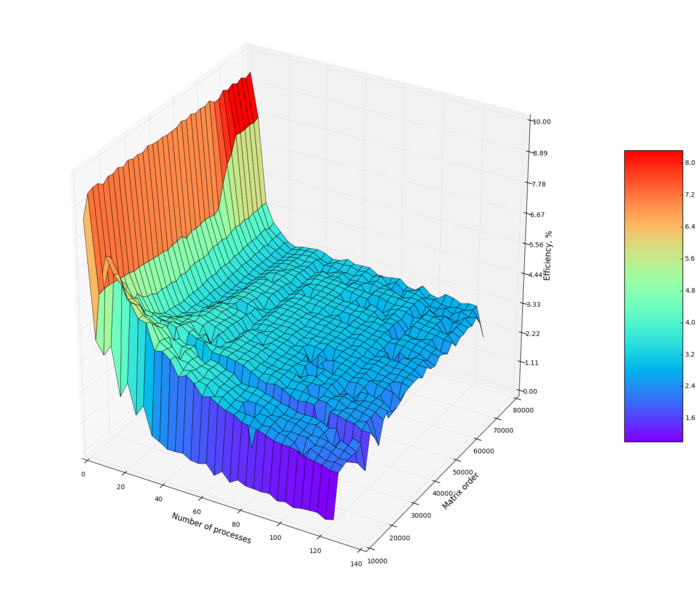
На следующих рисунках приведены графики производительности и эффективности выбранной реализации в зависимости от изменяемых параметров запуска.


Рисунок 1. Параллельная реализация нечеткого алгоритма С-средних. Изменение производительности в зависимости от числа процессоров и размера матрицы.
Рисунок 2. Параллельная реализация нечеткого алгоритма С-средних. Изменение эффективности реализации в зависимости от числа процессоров и размера матрицы.

Построим оценки масштабируемости выбранной реализации нечеткого алгоритма С-средних:

  • По числу процессов: 0.007. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска увеличивается.
  • По размеру задачи: -0.0016. При увеличении размера задачи эффективность уменьшается.
  • По двум направлениям: 0,000077. При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая.

Была использована следующая реализация алгоритма. 

   #include <mpi.h>
   #include <stdio.h>
   #include <iostream>
   #include <stdlib.h>
   #include <math.h>
   #include <string.h>
   #include <time.h>
   using namespace std;
   double **x; //input matrix of size (n x x_dim)
   int n;
   int x_dim;
   double **centroids; //cluster centroids matrix of size (n_cluster x x_dim)
   int n_cluster; // number of clusters
   double **w; //probability matrix of size (n x n_cluster)
   double **dist; //distances matrix of size (n x n_cluster)
   double eps; //max error
   double m; //parameter of algo
   int max_iter; // max num of iterations
   double **num;
   double *den;
   double *allden;
   double *err;
   double *total_err;
   int rank, size;
   double ** generateZerosMatrix(int r, int c){
       double ** arr = new double* [r];
       for (int i = 0; i < r; ++i){
           arr[i] = new double[c]();
       }
       return arr;
   }
   int generate_data()
   {
       //generate matrix
       x = generateZerosMatrix(n, x_dim);
       centroids = generateZerosMatrix(n_cluster, x_dim);
       w = generateZerosMatrix(n, n_cluster);
       dist = generateZerosMatrix(n, n_cluster);
       num = generateZerosMatrix(n_cluster, x_dim);
       //generate vectors
       den = new double [n_cluster]();
       allden = new double [n_cluster]();
       //for stopping algorithm
       err = new double;
       total_err = new double;
       srand(time(0));
       //initialize w randomly with restrictions
       for (int i = 0; i < n; ++i){
           double sum = 0;
           for (int j = 0; j < n_cluster; ++j){
               w[i][j] = rand();
               sum += w[i][j];
           }
           for (int j = 0; j < n_cluster; ++j){
               w[i][j] /= sum;
           }
       }
       //initialize x randomly
       for (int i = 0; i < n; ++i)
           for (int j = 0; j < x_dim; ++j)
               x[i][j] = rand();
       return 0;
   }
   double make_iteration() {
       // calculate centroids centers
       for (int i = rank; i < n; i+=size)
           for (int j = 0; j < n_cluster; ++j){
               double mu = pow(w[i][j], m);
               den[j] += mu;
               for (int k = 0; k < x_dim; ++k)
                   num[j][k] = mu * x[i][k];
           }
       MPI_Allreduce(den, allden, n_cluster, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
       for (int j=0; j < n_cluster; ++j)
           MPI_Allreduce(num[j], centroids[j], x_dim, MPI_DOUBLE, MPI_SUM, MPI_COMM_WORLD);
       for (int i = 0; i < n_cluster; ++i)
           for (int j = 0; j < x_dim; ++j)
               centroids[i][j] /= allden[i];
       // calculate distances and probabilities, check stop conditions
       double err = 0.0;
       for (int i = rank; i < n; i+=size)
           for (int j = 0; j < n_cluster; ++j){
               for (int k = 0; k < x_dim; ++k)
                   dist[i][j] += (x[i][k] - centroids[j][k]) * (x[i][k] - centroids[j][k]);
               double w_prev = w[i][j];
               for (int k = 0; k < n_cluster; ++k)
                   w[i][j] += dist[i][j] / dist[i][k];
               w[i][j] = 1.0 / pow(w[i][j], 1.0 / (m - 1));
               err = fmax(err, abs(w_prev - w[i][j]));
           }
       return err;
   }
   int FCM(){
       *total_err = eps+1;
       int cur_iter = 0;
       while (cur_iter < max_iter && *total_err > eps){
           *err = make_iteration();
           MPI_Allreduce(err, total_err, 1, MPI_DOUBLE, MPI_MAX, MPI_COMM_WORLD);
           cur_iter++;
       }
       return cur_iter;
   }
   void clearMatrix(double ** matr, int r, int c){
       for (int i = 0; i < r; ++i){
           delete [] matr[i];
       }
       delete [] matr;
   }
   int memory_free(){
       clearMatrix(x, n, x_dim);
       clearMatrix(centroids, n_cluster, x_dim);
       clearMatrix(w, n_cluster, n);
       clearMatrix(num, n_cluster, x_dim);
       clearMatrix(dist, n, n_cluster);
       delete [] den;
       delete [] allden;
       delete err;
       delete total_err;
       return 0;
   }
   int main(int argc, char **argv){
       MPI_Init(&argc, &argv);
       MPI_Comm_size(MPI_COMM_WORLD, &size);
       MPI_Comm_rank(MPI_COMM_WORLD, &rank);
       int n_repeat = strtol(argv[1], NULL, 10);
       int nx_min = strtol(argv[2], NULL, 10);
       int nx_max = strtol(argv[3], NULL, 10);
       int step = strtol(argv[4], NULL, 10);
       x_dim = strtol(argv[5], NULL, 10);
       m = strtod(argv[6], NULL);
       n_cluster = strtol(argv[7], NULL, 10);
       max_iter = strtol(argv[8], NULL, 10);
       eps = strtod(argv[9], NULL);
       //for all input matrix sizes
       for (n = nx_min; n <= nx_max; n += step){
           double start, finish, time_elapsed_iter=0;
           int total_iterations = 0;
           //repeat for getting mean value
           for (int i = 0; i < n_repeat; ++i) {
               generate_data();
               MPI_Barrier(MPI_COMM_WORLD);
               start = MPI_Wtime();
               total_iterations += FCM();
               finish = MPI_Wtime();
               memory_free();
               time_elapsed_iter += (finish-start);
           }
           time_elapsed_iter /= total_iterations;
           if (rank == 0) {
               cout << n << " " << size << " " << time_elapsed_iter << endl;
           }
       }
       MPI_Finalize();
   }

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма


3 Литература

  1. ↑ | J. C. Dunn. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics, volume 3,1973 - Issue 3, pp 32-57
  2. ↑ | Нейский И.М. Классификация и сравнение методов кластеризации.// Интеллектуальные технологии и системы. Сборник учебно-методических работ и статей аспирантов и студентов. – М.: НОК «CLAIM», 2006. – Выпуск 8. – С. 130-142.
  3. ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Gkhazeeva/Нечеткий_алгоритм_C_средних&oldid=21436