На перевод

1 Прямая подстановка (вещественный вариант)

1.1 Программная реализация

1.1.1 Особенности реализации последовательного алгоритма

В простейшем варианте метод прямой подстановки на Фортране можно записать так:

        Y(1) = B(1) 
	DO  I = 2, N-1
		S = B(I)
		DO  J = 1, I-1
			S = S - DPROD(L(I,J), Y(J))
		END DO		
	END DO

При этом для реализации режима накопления переменная [math]S[/math] должна быть двойной точности.

1.1.2 Описание локальности данных и вычислений

1.1.2.1 Описание локальности реализации алгоритма

1.1.2.1.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Прямой ход метода Гаусса решения СЛАУ. Общий профиль обращений в память

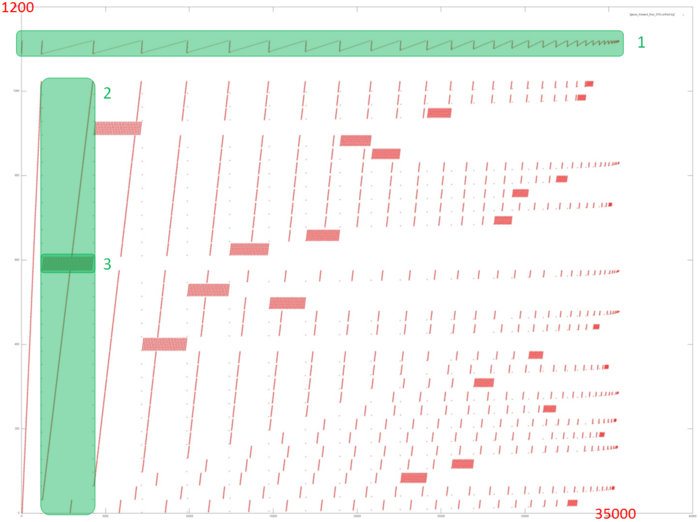
На рисунке 12.1 представлен профиль обращений в память для прямого хода метода Гаусса решения СЛАУ. Из исходного кода, как и из рисунка, видно, что в программе задействовано 2 основных массива: профиль обращений к элементам первого выделен зеленым (фрагмент 1); все остальные обращения происходят к элементам второго массива. Видно, что общий профиль всей программы устроен достаточно сложно. Основное, что можно заметить из данного рисунка, – это итерационная природа профиля, причем каждая следующая итерация содержит меньше обращений. Это особенно хорошо видно по фрагменту 1.

Далее, как известно, в прямом ходе Гаусса на каждой итерации отбрасывается из рассмотрения одна из строк СЛАУ. Это отчетливо видно и на рис. 12.1: на каждой итерации (одна из них выделена как фрагмент 2) выполняется серия обращений, связанных с отбрасываемой строкой (фрагмент 3), после чего обращения к этим элементам больше не выполняются. Также можно заметить, что фрагменты, подобные фрагменту 3, на каждой последующей итерации становятся все меньше, как по числу обращений, так и по числу элементов, к которым происходят обращения.

Однако на основе подобной общей картины очень сложно дать даже качественные оценки локальности. Перейдем к более подробному рассмотрению фрагмента 1, соответствующего обращениям к одному из двух массивов.

Рисунок 12.2. Фрагмент 1 (профиль обращений к первому массиву)

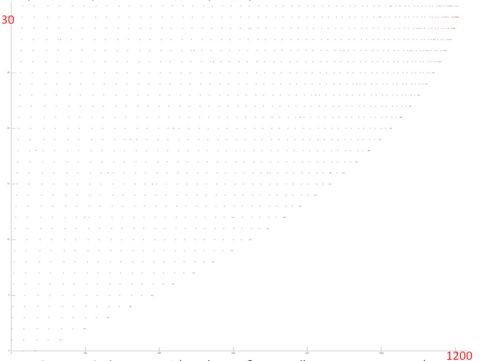
На рис. 12.2 показан отдельно фрагмент 1, выделенный на рис. 12.1 зеленым. Наблюдается довольно интересная картина: исходя из рис. 12.1, складывалось впечатление, что данный профиль образуется чередованием итераций двух разных циклов, причем итерация первого цикла заметно короче итераций второго цикла. На самом же деле, из рис. 12.2 можно увидеть, что профиль состоит из однотипных итераций, в рамках которых производится последовательный перебор элементов массива. При этом на каждой следующей итерации отбрасывается элемент с минимальным индексом. Иллюзия наличия двух разных циклов обусловлена исключительно числом обращений к другому массиву – когда число таких обращений велико, итерация данного фрагмента кажется длиннее. При этом во фрагменте 1 (как видно на рис. 12.2) число обращений всего лишь около 1200, тогда как весь профиль обращений состоит из 34 тысяч. То есть на долю обращений к первому массиву приходится всего 3.5% всех обращений в программе.

Поскольку основа данного профиля – последовательный перебор элементов массива, можно сказать, что данный фрагмент обладает высокой пространственной локальностью. А поскольку итераций с перебором элементов достаточно много, также видно, что и временна́я локальность достаточно высока.

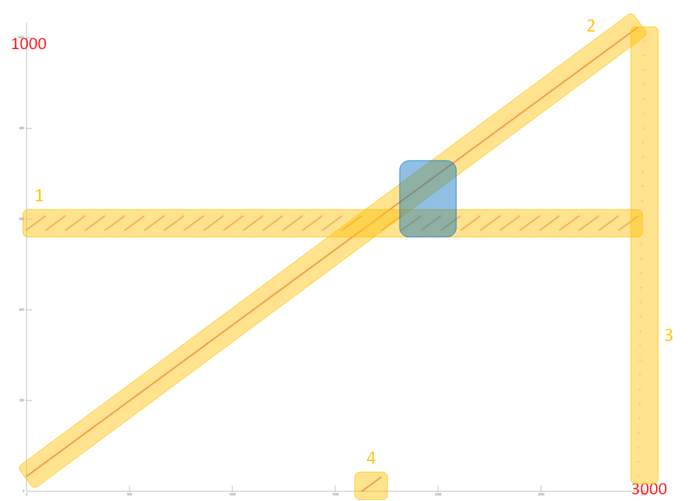
Теперь перейдем к рассмотрению профиля обращений ко второму массиву, который значительно больше и сложнее первого профиля. На рис. 12.3 отдельно представлен фрагмент 2, выделенный на рис. 12.1. Такой фрагмент устроен из четырех частей, отмеченных на рисунке оранжевым.

Рисунок 12.3. Фрагмент 2 (итерация профиля обращений ко второму массиву)

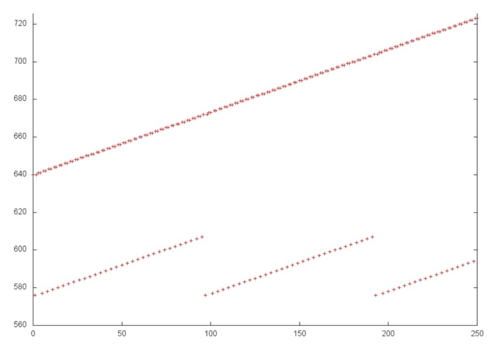
Часть 1 очень похожа на повторяющийся последовательный перебор одного и того же небольшого числа элементов в цикле. При более близком рассмотрении можно убедиться, что это действительно так. На рис. 12.4 показано приближение фрагмента 2, выделенное на рис. 12.3 синим цветом. Также на этом рисунке видно, что часть 2 представляет собой практически полное подобие последовательного перебора всех элементов данного массива. Таким образом, обе эти части обладают высокой пространственной локальностью (из-за последовательного перебора). При этом часть 1 обладает также высокой временной локальностью, поскольку перебор повторяется в цикле, в отличие от части 2, где к каждому элементу выполняется только одно обращение.

Часть 3 состоит всего из нескольких обращений и представляет собой перебор всех элементов массива, выполненных с достаточно большим шагом, гораздо большим, чем в части 2. В данном случае, из-за достаточно большого шага, наблюдается невысокая пространственная локальность и отсутствие временно́й локальности, так как перебор выполняется единожды.

Часть 4 представляет собой последовательный перебор части массива, по размеру соответствующей числу отброшенных из рассмотрения элементов; чем ближе к концу профиля, тем больше обращений расположено в части 4. Эта часть обладает теми же свойствами локальности, что и часть 2. Отличие заключается в числе обращений, однако в данном случае это не оказывает сильное влияние на локальность.

При рассмотрении фрагмента 2 в целом основное влияние оказывают части 1 и 2, поэтому можно утверждать, что это фрагмент обладает достаточно высокой и пространственной, и временно́й локальностью. Однако на последующих итерациях (см. рис. 12.1) локальность в целом будет постепенно снижаться, поскольку на каждой итерации отбрасывается из рассмотрения некоторая часть элементов.

Рисунок 12.4. Приближение фрагмента 2

1.1.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel1). Условия запуска описаны здесь.

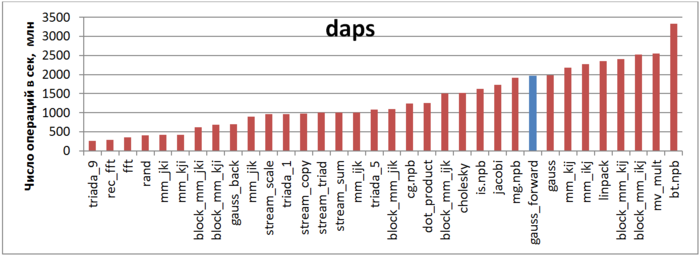
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рисунке 12.5 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что отмеченный синий столбец, соответствующий прямому ходу метода Гаусса, расположен в правой части и показывает достаточно высокую производительность, немного ниже производительности теста Линпак. Также отметим, что значение daps для данной задачи практически совпадает со значением daps для всего метода Гаусса (столбец «gauss»), объединяющего как прямой, так и обратный ход. Это связано с тем, что обратный ход состоит из гораздо меньшего числа обращений, нежели прямой ход, поэтому оказывает меньшее влияние.

Рисунок 12.5. Сравнение значений оценки daps

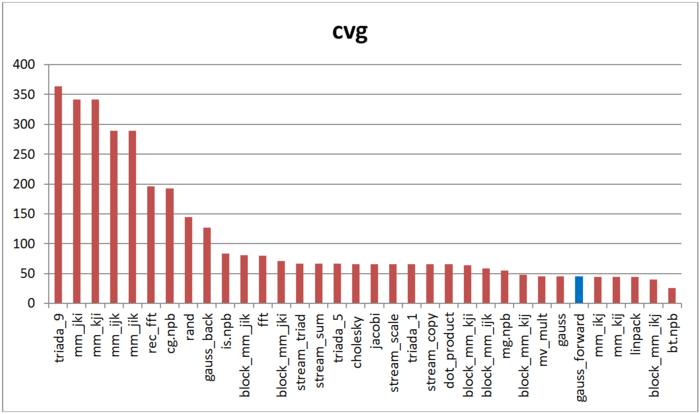
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

На рисунке 12.6 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, как и в случае с оценкой daps, прямой ход метода Гаусса обладает высокой локальностью. Причем согласно данной оценке тест Линпак показывает практически те же результаты. Отметим, что снова значение оценки для отдельно прямого хода и совокупности прямого и обратного ходов (столбец «gauss») совпадают.

Рисунок 12.6. Сравнение значений оценки cvg

1.1.4 Масштабируемость алгоритма и его реализации

1.1.4.2 Описание масштабируемости реализации алгоритма

Рисунок 1. Масштабируемость параллельной реализации метода Гаусса (прямой ход) Максимальная производительность.

Рисунок 2. Масштабируемость параллельной реализации метода Гаусса (прямой ход) Максимальная эффективность.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [4 : 256]
• размер матрицы [1024 : 5120]

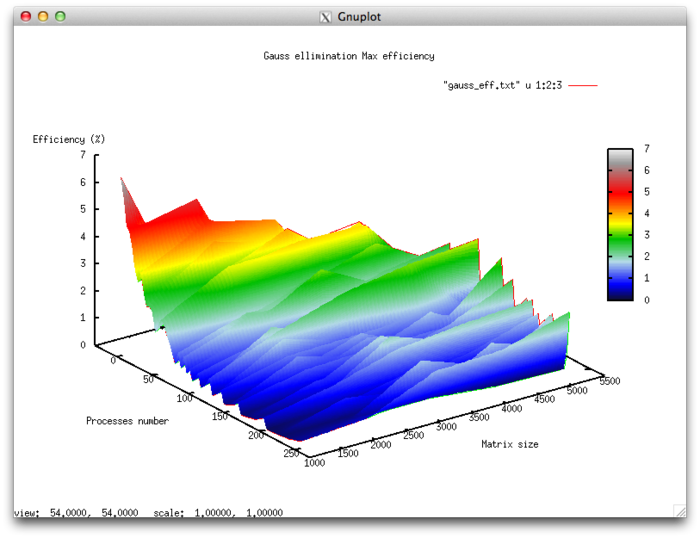
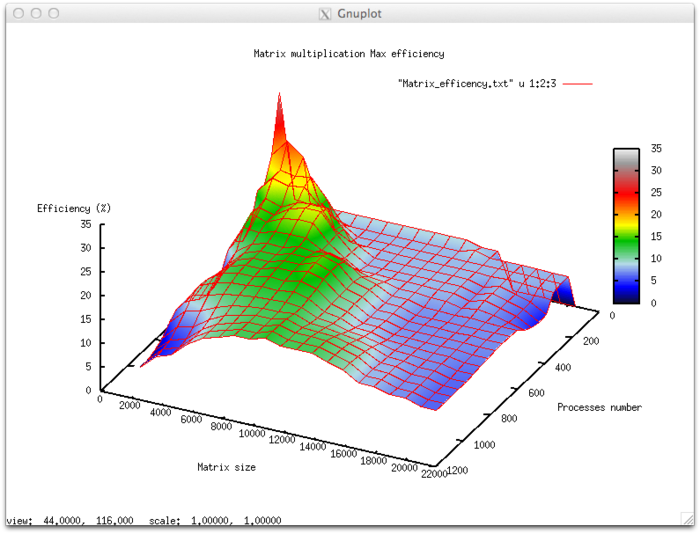
Эффективность выполнения реализации алгоритма

• Минимальная эффективность 0,11 %
• Максимальная эффективность 6.65%

Оценка масштабируемости

• По числу процессов: -0.000101 – при увеличении числа процессов эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Учитывая разницу между максимальным и минимальным значением эффективности в 6,5% можно сделать вывод, что на рассмотренной области снижение эффективности, скорее всего, достаточно равномерное. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. Могут присутствовать области возрастания эффективности, на всех рассмотренных размерах матрицы. Это может объясняться увеличением вычислительной сложности задачи, что при постоянных накладных расходах на организацию параллельного взаимодействия приводит к общему увеличению эффективности работы.
• По размеру задачи:-0.00674– при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области. Это может свидетельствовать о том, что при увеличении размера задачи возрастают и накладные расходы на организацию параллельного взаимодействия. Так как интенсивность снижения эффективности по этому направлению выше, чем по направлению числа процессов, скорее всего падение интенсивности значительно при малом числе процессов более интенсивное, чем в присутствующих областях возрастания эффективности при большом числе процессов.
• По двум направлениям: -6.621e-05 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности очень мала. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 6,5 % говорит о том, что если на поверхности присутствуют области с очень интенсивным изменением эффективности, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.

Исследованная параллельная реализация на языке C

2 Перемножение плотных неособенных матриц (последовательный вещественный вариант)

2.1 Программная реализация

2.1.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм умножения матриц на Фортране можно записать так:

         
	DO  I = 1, M
        DO  J = 1, L
		S = 0.
		DO  K = 1, N
			S = S + DPROD(A(I,K), B(K,J))
		END DO	
	        C(I, J) = S
        END DO
	END DO

При этом для реализации режима накопления переменная [math]S[/math] должна быть двойной точности.

2.1.2 Описание локальности данных и вычислений

2.1.2.1 Описание локальности реализации алгоритма

2.1.2.1.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Профили обращений для 6 вариантов перемножения матриц

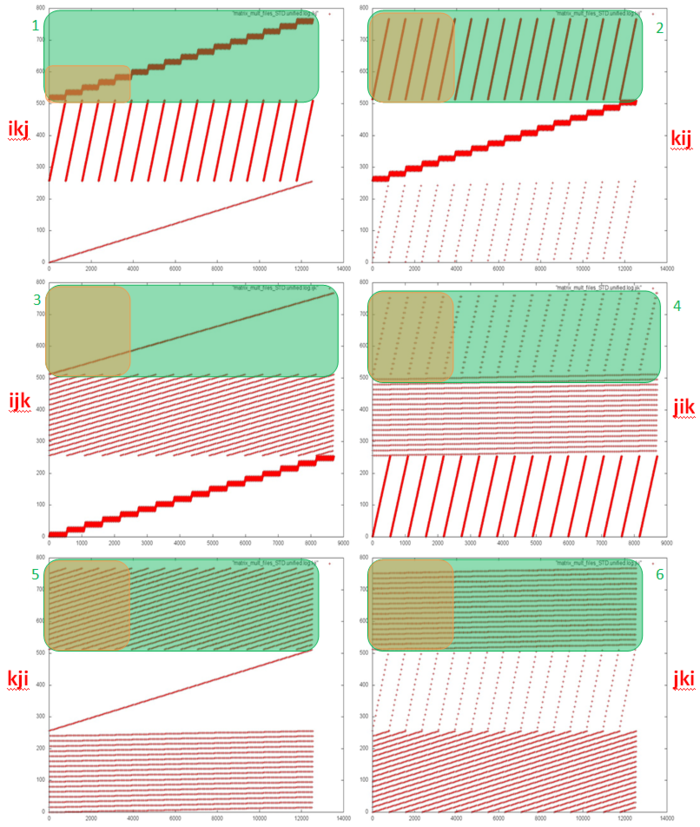
На рисунке 12.1 представлены 6 профилей обращений для различных вариантов классического перемножения матриц (в зависимости от выбранного порядка циклов). На каждом профиле хорошо выделяются фрагменты профилей для 3-х массивов, используемых в программе. При этом порядок обращений к разным массивам во всех 6 вариантах один и тот же; т.е. взаимодействие между массивами везде устроен одинаково. В этом случае отличия в локальности задаются внутренним строением фрагментов профиля для каждого массива в отдельности.

Исходя из исходного кода, можно увидеть, что всего встречается 6 разных видов фрагментов для отдельных массивов (эти виды выделены на рис. 12.1 зеленым). Стоит сделать два уточнения: 1) профиль для результирующего массива С всегда в 2 раза больше, поскольку к элементам этого массива всегда происходят по два обращения подряд; 2) если во внутреннем цикле используется элементы массива, то обращение к этому элементу выносится за пределы внутреннего цикла (в цикле используется скалярная переменная вместо него).

Также заранее отметим, что рисунки по профилям получаются следующим образом: строится рисунок по общему профилю, после чего из него оставляется только часть для рассматриваемого массива. Доля обращений к одному массиву может меняться, поэтому и частота обращений на каждом рисунке может в значительной степени отличаться.

Рассмотрим подробнее каждый из данных 6 фрагментов на примере массива С.

Фрагмент 1. На рисунке 12.2 показано начало фрагмента 1 (здесь и далее начало фрагмента соответствует выделенной оранжевой области на рис. 12.1). Можно увидеть, что данный фрагмент устроен достаточно просто: выполняется перебор некоторого блока элементов массива, затем данный перебор циклически повторяется. После этого происходит переход к следующему блоку элементов массива, и выполняется тот же перебор в цикле.

Если рассмотреть фрагмент более подробно (рисунок 12.3), можно увидеть, что каждый перебор является на самом деле последовательным перебором, при этом к каждому элементу происходит обращение дважды.

В результате можно сделать вывод, что фрагмент 1 обладает высокой пространственной локальностью (из-за последовательного перебора и последовательной смены блоков перебора), а также высокой временно́й локальностью (из-за двойного обращения к элементам, а также сгруппированности всех обращений к одному элементу в рамках одного блока перебора).

Рисунок 12.2. Начало фрагмента 1

Рисунок 12.3. Начало фрагмента 1, первые 3 итерации

Фрагмент 2. На рисунке 12.4 представлено начало фрагмента 2. Видно, что данный фрагмент также представляет собой перебор элементов массива в цикле, однако в данном случае на каждой итерации цикла перебираются сразу все элементы массива, а не только элементы одного блока. При более подробном рассмотрении итерации (рис. 12.5) видно, что здесь также происходит именно последовательный перебор, и также к каждому элементу обращение происходит дважды (поскольку это массив С).

Рисунок 12.4. Начало фрагмента 2

Рисунок 12.5. Начало фрагмента 2, часть первой итерации

Такой фрагмент также обладает высокой пространственной локальностью, однако временна́я локальность несколько ниже, чем во фрагменте 1. Это связано с тем, что на каждой итерации цикла перебираются все элементы массива, а не только отдельный блок, т.е. повторные обращения происходят реже.

Фрагмент 3. Начало данного фрагмента представлено на рисунке 12.6. Данный профиль является последовательным перебором всех элементов массива, однако более подробное рассмотрение показывает, что к каждому элементу происходит обращение дважды, при этом между обращениями происходит достаточно много других обращений. Это связано с указанным ранее замечанием касательно вынесения повторяющегося обращения за предел внутреннего цикла.

Рисунок 12.6. Начало фрагмента 3

Рисунок 12.7. Начало фрагмента 3, первые несколько обращений

Такой фрагмент также обладает высокой пространственной локальностью, однако очень низкой временно́й, поскольку к каждому элементу обращение происходит только два раза.

Фрагмент 4. По началу фрагмента 4 видно, что профиль снова состоит из перебора всех элементов массива, однако на этот раз перебор не последовательный, а с некоторым шагом. Также можно заметить, что на каждой новой итерации перебор с шагом начинается с элемента, индекс которого немного больше, чем на предыдущей итерации. В данном случае нет нужды рассматривать профиль более подробно, поскольку из данного рисунка можно получить всю необходимую информацию.

По сравнению с предыдущим фрагментом, данный профиль обладает более низкой пространственной локальностью, поскольку перебор элементов идет с шагом, и также очень низкой временно́й локальностью, поскольку на каждой итерации происходят обращения к новым элементам.

Рисунок 12.8. Начало фрагмента 4

Фрагмент 5. В отличие от предыдущих фрагментов, исходя из визуализации начала данного фрагмента (рис. 12.8), сложно сделать выводы относительно структуры обращения в память. Однако более подробное рассмотрение (рис. 12.9) показывает, что данный профиль практически идентичен профилю предыдущего фрагмента. Более того, фрагмент 5 на самом деле состоит из итерационно повторяющихся фрагментов 4.

Рисунок 12.9. Начало фрагмента 5

Рисунок 12.10. Начало фрагмента 5, первые несколько итераций

Данный фрагмент обладает по сравнению с фрагментом 4 практически такой же пространственной локальностью, однако более высокой временной локальностью. Причина в обоих случаях одна – в данном случае тот же набор обращений повторяется несколько раз.

Фрагмент 6. Данный фрагмент, представленный на рис. 12.11 и 12.12, так же сильно напоминает фрагмент 5, но с одним отличием. Во фрагменте 5 несколько раз повторяется фрагмент 4, в рамках которого выполняется несколько итераций, и на каждой итерации внутри фрагмента 4 используются разные элементы (поскольку первый элемент сдвигается на 1). В случае данного фрагмента выполняются все те же итерации, но в перемешанном виде. Сначала выполняются все итерации, начинающиеся с одного и того же элемента; затем все итерации, который начинаются с элемента, чей индекс идет следующим; и т.д.

Такой фрагмент обладает более высокой и пространственной, и временно́й локальностью по сравнению с фрагментом 5, поскольку обращения в одним и тем же элементам расположены ближе друг к другу в профиле.

Рисунок 12.11. Начало фрагмента 6

Рисунок 12.12. Начало фрагмента 6, первые несколько итераций

В итоге можно сказать, что наиболее низкой локальностью в целом обладают фрагменты 5 и 6. Фрагмент 4 также обладает низкой локальностью, однако содержит значительно меньшее число обращений, а значит, привносит меньший вклад в общий профиль обращений. Это позволяет определить, что наименее эффективными с точки зрения работы с памятью являются варианты kji и jki, поскольку каждый из них содержит фрагменты 5 и 6. Далее идут варианты ijk и jik – в них по одному такому фрагменту. Самые лучшие варианты – ikj и kij.

2.1.2.1.2 Количественная оценка локальности

Основные фрагменты реализации, на основе которых были получены количественные оценки, приведены здесь (функция Kernel***, где *** - порядок циклов (напр., KernelIJK) ). Условия запуска описаны здесь.

Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

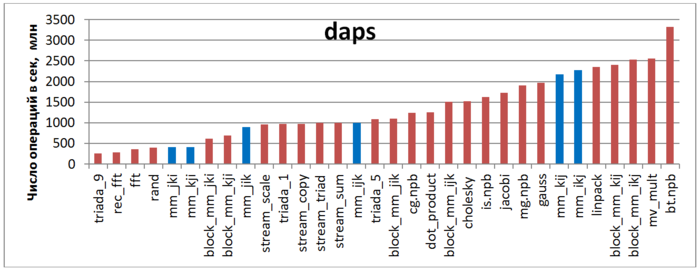
На рисунке 12.13 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что, как и предполагалось наиболее эффективными являются варианты kij,ikj. Заметно хуже результат у вариантов jik,ijk, при этом эти варианты практически равны между собой. Самый плохой результат ожидаемо у вариантов jki,kji.

Рисунок 12.13. Сравнение значений оценки daps

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

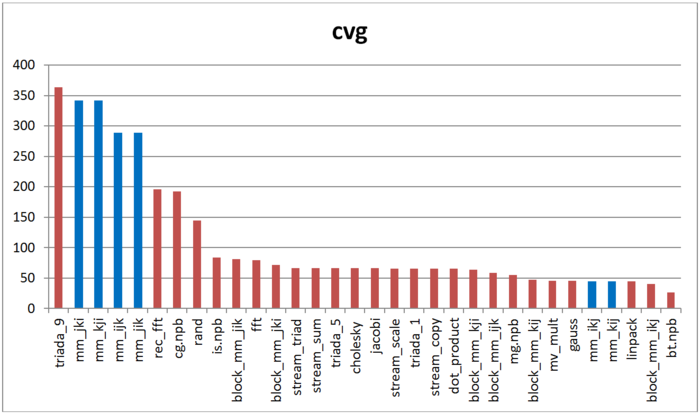
На рисунке 12.14 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Относительное сравнение результатов по cvg в целом повторяет результаты daps.

Рисунок 12.14. Сравнение значений оценки cvg

2.1.4 Масштабируемость алгоритма и его реализации

2.1.4.2 Описание масштабируемости реализации алгоритма

Рисунок 1. Параллельная реализация произведения матриц Максимальная производительность.

Рисунок 2. Параллельная реализация произведения матриц Максимальная эффективность.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [4 : 1024]
• размерность матрицы [1024 : 20480]

Эффективность выполнения реализации алгоритма

• Минимальная эффективность 4,71%
• Максимальная эффективность 31,72%

Оценка масштабируемости

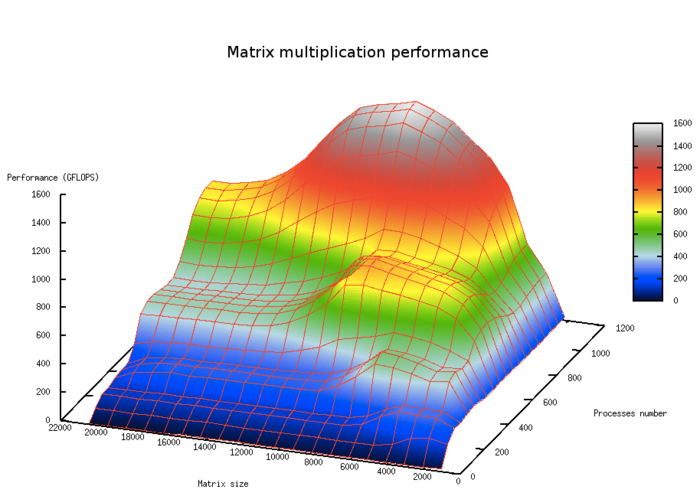
• По числу процессов: -0.0436 – при увеличении числа процессов эффективность убывает достаточно интенсивно на всей рассмотренной области изменений параметров запуска. Уменьшение эффективности на рассмотренной области работы параллельной программы звязано с увеличением числа пересылок с ростом числа процессов и как следствие ростом накладных расходов на организацию вычислений. Присутствует область, на которой при увеличении числа процессов эффективность возрастает, но при дальнейшем росте продолжает снижаться. Это объясняется декомпозицей данных, при которой наступает момент, когда размер матрицы позволяет блокам укладываться в КЭШ-память. Так же это подтверждает проявление этого явления, но со смещением по числу процессов, и при увеличении вычислительной сложности задачи.
• По размеру задачи: -0.0255 – при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. Присутствует область возрастания эффективности, на всех рассмотренных размерах матрицы. Это объясняется тем, что при малом размере задачи данные хорошо укладываются в КЭШ память, что приводит к высокой эффективности работы приложения при малом размере задачи. При дальнейшем увеличении размера эффективность уменьшается при выходе за границы КЭШ-памяти.
• По двум направлениям: -0.000968 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, интенсивность уменьшения эффективности не очень высока. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 25% говорит о том, что уменьшение эффективности по всей области довольно равномерное, но интенсивно лишь в не очень больших участках по площади. На остальной области значений параметров изменения эффективности не столь значительны и находятся на приблизительно одном и том же уровне.

Реализация алгоритма на языке C

3 Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки

3.1 Программная реализация

3.1.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм на Фортране можно записать так, что входной и выходной массивы совпадают (здесь использован массив X):

         
        subroutine STEP2(x,y,pov)
        complex x, y, pov, u, v
        u = x + y
        v = (x-y)*pov
        x = u
        y = v
        return
        end
        subroutine FFT2(X, POV, N, N2, L)
C
C L = Log2N
C N2 = N/2
C
        complex X(0:N-1), POV(0:N2-1)
        DO I = 0, L-1
            DO J = 0, N2/2**I-1
            DO K = 0, 2**I-1
                call STEP2(X(2*J*2**I+K)), X(2*J*2**I+2**I+K), POV(J*2**I-1))
            END DO
            END DO
         END DO
         return
         end

Здесь предполагается, что поворотные множители первого шага (они потом используются и на последующих шагах) предвычислены заранее и лежат в элементах массива POV (а в его нулевом элементе - единица). К сожалению, подавляющее большинство реализаций простого алгоритма Кули-Тьюки вычисляет поворотные множители одновременно с вычислением "бабочки", что её значительно замедляет.

3.1.2 Описание локальности данных и вычислений

3.1.2.1 Описание локальности реализации алгоритма

3.1.2.1.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память

На рисунке 12.1 представлен профиль обращений в память для нерекурсивной реализации быстрого преобразования Фурье. Исходя из исходного кода, можно увидеть, что в программе задействовано 3 массива. Фрагменты двух из них отмечены на рис. 12.1 зеленым, к третьему массиву относится вся остальная часть профиля.

Фрагменты 1 и 2 образованы обращениями соответственно к входному и выходному массиву. Из рисунка видно, что в обоих случаях фрагменты представляют собой аналог последовательного перебора. Анализ исходного кода показывает, что это действительно так: в обоих случаях в рамках одного цикла последовательно перебираются все элементы массива. Такие профили обладают высокой пространственной локальностью и очень низкой временной, поскольку повторные обращения просто отсутствуют.

Гораздо интереснее устроен последний фрагмент. Его можно разбить на 4 этапа, которые выделены на рис. 12.1 оранжевым цветом. Первый этап по времени совпадает с фрагментом 1, и сам профиль также похож на последовательный перебор. Из исходного кода видно, что обращения этапа 1 – это запись в массив data либо 0, либо значений, считываемых во фрагменте 1 из массива dIn:

for( i = 0; i < nn; i++ ) {
data [ i ] = 0;
data[ i * 2 + 1 ] = dIn[ i ];
}

Видно, что обращения этапа 1 также образуют последовательный перебор. Аналогична ситуация с этапом 4, однако там на каждое 1 обращение фрагмента 1 приходится 4 последовательных обращений этапа 4.

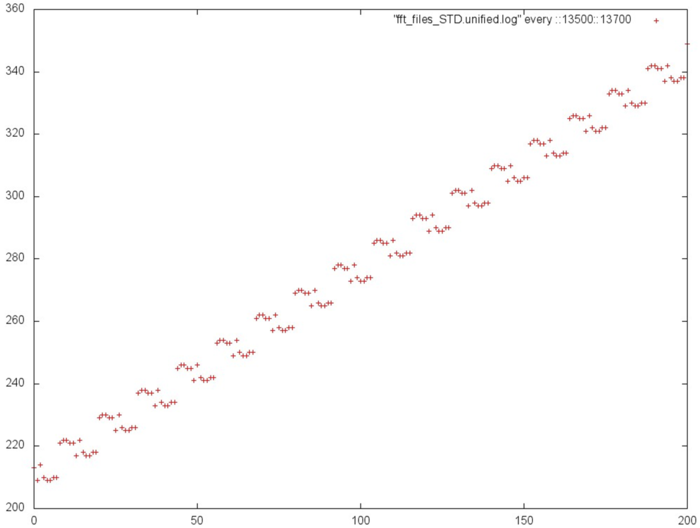
Рассмотрим более подробно этап 2 (рис. 12.2). Можно увидеть, что в начале этого этапа происходят обращения по всему массиву, но чем ближе к концу этапа, тем ближе к концу массива происходят обращения. Видно, что часть обращений (кривая внизу рисунка) расположены близко друг к другу, а остальные обращения разбросаны достаточно далеко и образуют нечто похожее на случайный доступ.

Рисунок 12.2. Основной фрагмент, этап 2

Исходный код, в котором происходят обращения данного этапа, устроен следующим образом:

while( i < n ) {
if( j > i ) {
tempr = data[ i ]; data[ i ] = data[ j ]; data[ j ] = tempr;
tempr = data[ i + 1 ]; data[ i + 1 ] = data[ j + 1 ]; 
data[ j + 1 ] = tempr;
}
m = n >> 1;
while( ( m >= 2 ) && ( j > m ) ) {
j = j - m;
m = m >> 1;
}
j = j + m;
i = i + 2;
}

Можно увидеть, что действительно обращения выполняются по двум независимым индексам – на основе переменных i и j; при этом обращения на основе индекса i образуют кривую внизу рис. 12.2, а обращения на основе индекса j – остальные, разбросанные по всему массиву обращения.

Стоит заметить, что обращения на основе индекса j не образуют случайный доступ, а подчиняются определенному закону выбора следующего элемента. Однако с точки зрения качественной оценки локальности подобные фрагменты похожи.

Таким образом, этап 2 состоит из двух фрагментов на основе двух разных индексов. Первый из них которых обладает высокой пространственной локальностью (последовательный перебор элементов) и низкой временной (к каждому элементу происходит только два обращения). Второй обладает и достаточно низкой пространственной (элементы расположены далеко друг от друга, за исключением конца этапа), и низкой временной (к каждому элементу происходит только два обращения) локальностью.

Теперь перейдем к рассмотрению самого длительного этапа 3. Отдельно данный фрагмент представлен на рис. 12.3. Исходя из рисунка, можно увидеть, что данный фрагмент состоит из нескольких итераций, причем первая итерация состоит из единичного перебора элементов массивов с некоторым шагом, вторая итерация состоит из двух проходов с одинаковым шагом (большим, чем на первой итерации), третья – из 4-х проходов и т.д., пока число проходов на итерации не начинает уменьшаться в обратную сторону. Итерации разделены на рис. 12.3 оранжевыми линиями.

Рисунок 12.3. Основной фрагмент, этап 3

Видно, что внутри каждой итерации проходы обладают одинаковой структурой, а также можно предположить, что при переходе к новой итерации шаг изменяется в два раза, что и подтверждает анализ исходного кода. Также можно увидеть, что каждая итерация состоит из примерно одного числа обращений (размер выделенных оранжевыми линиями частей одинаковы).

Первая итерация похожа на последовательный перебор элементов массива, поэтому она обладает высокой пространственной и низкой временной локальностью. При увеличении шага пространственная локальность становится хуже, однако неясно, каким образом меняется временная локальность – это зависит от того, происходит ли повторный проход по тем же элементам или нет. Анализ исходного кода показывает, что каждый проход выполняется над своими элементами, поэтому временная локальность остается такой же низкой. Однако отметим, что на каждой итерации используются один и те же элементы, поэтому в целом повышает временную локальность.

Более подробное изучение каждого прохода (рис. 12.4, на которой приближена выделенная зеленым часть рис. 12.3) показывает, что он обладает более сложной структурой, чем просто перебор элементов массива с некоторым шагом: в данном случае происходит серия близких друг к другу обращений, и затем сдвиг на некоторый шаг. Это приводит к некоторому улучшению как пространственной, так и временной локальности.

Рисунок 12.4. Основной фрагмент, небольшая часть этапа 3

3.1.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel). Условия запуска описаны здесь.

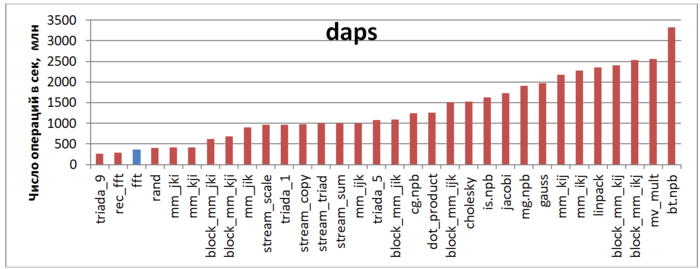
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

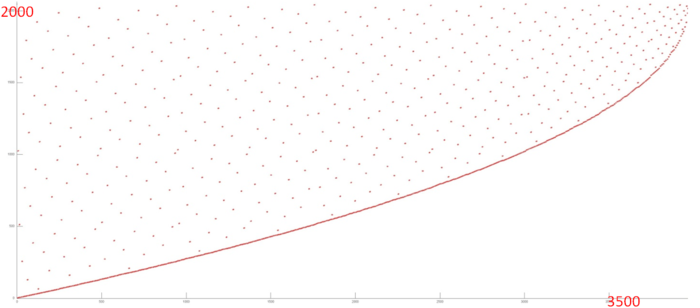
На рисунке 12.5 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что данная оценка показывает низкую производительность, на уровне случайного доступа в память (rand).

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность

Рисунок 12.5. Сравнение значений оценки daps

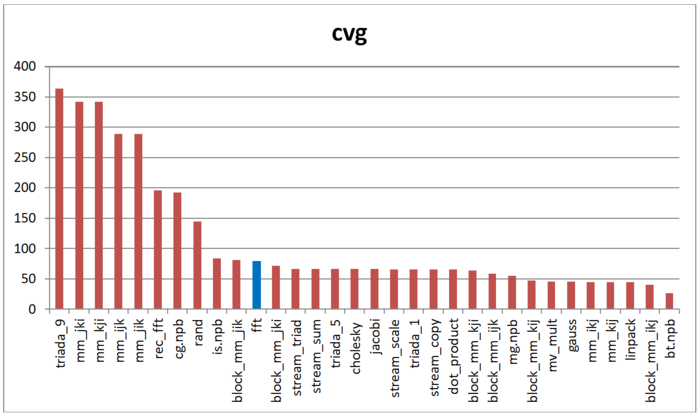
На рисунке 12.6 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, данная реализация БПФ демонстрирует несколько лучшую локальность по сравнению со случайным доступом или рекурсивной версией, в отличие от оценки daps, результаты которой для данных программ практически совпадали. На данный момент остается неясным, чем обусловлено это различие. Однако стоит отметить, что значение локальности cvg также остается в нижней части таблицы.

Рисунок 12.6. Сравнение значений оценки cvg

3.1.6 Выводы для классов архитектур

Граф простого алгоритма Кули-Тьюки лучше всего из коммуникационных сетей отображается на сеть типа гиперкуб. Распространённость БПФ в методах решения различных задач поэтому привела к популярности идеи вычислительных систем с сетью типа гиперкуб в начале развития различных параллельных вычислительных систем. В настоящее время, однако, массово такие вычислительные системы не используются по физическим причинам, делающим гиперкуб большой размерности труднореализуемым на практике. Как видно из графа, при простом его разбиении на части прямыми, параллельными оси шагов, на первых шагах алгоритма обмены между разными частями будут отсутствовать, но, начиная с некоторого момента, они станут составлять величину, сопоставимую с количеством арифметических операций. Этого, однако, можно избежать, если примерно посередине алгоритма переупорядочить все данные. В графе это будет соответствовать смене разбиения на части. При выполнении указанных рекомендаций, алгоритм можно будет реализовать более эффективно, чем в настоящее время, и на архитектурах типа кластерной и на других архитектурах, реализующих разбиение процесса на независимые ветви.

3.1.7 Существующие реализации алгоритма

Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки весьма распространён среди начинающих, использующих БПФ, и его сравнительно легко можно найти в Интернете с помощью поисковых сайтов. Как правило, эти реализации не используют описанных выше приёмов улучшения эффективности вычислений - ни для последовательной, ни для параллельной архитектуры. Связано это с тем, что сам по себе простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки проигрывает другим алгоритмам Кули-Тьюки, которые используют специфику, например, чётных степеней двойки, и потому более экономичны. Поэтому большинство исследователей, которым нужны более быстрые программы БПФ, не улучшают эффективность этого алгоритма, а меняют его на другой. Это же рекомендуем делать и читателям.