Участник:Ilya365365/Алгоритм кластеризации категориальных данных
Содержание
1 Свойства и структура алгоритма CLOPE
1.1 Общее описание алгоритма CLOPE
Алгоритм CLOPE решает задачу кластеризации категориальных данных. Здесь и далее под категориальными данными понимаются качественные характеристики объектов, измеренные в шкале наименований, то есть при сравнении категориальных данных указывается только, одинаковы или нет объекты относительно данного признака.
Алгоритм CLOPE работает с транзакциями. Под термином транзакция понимается произвольный набор объектов, например, список ключевых слов статьи, товары, купленные в супермаркете, множество симптомов пациента, характерные фрагменты изображения и так далее. Задача кластеризации транзакционных данных состоит в получении такого разбиения всего множества транзакций, чтобы похожие транзакции оказались в одном кластере, а отличающиеся друг от друга – в разных кластерах.
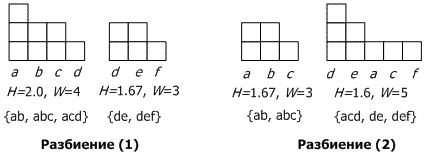
В основе алгоритма кластеризации CLOPE лежит идея максимизации глобальной функции стоимости, которая повышает близость транзакций в кластерах при помощи увеличения параметра кластерной гистограммы.Для примера рассмотрим выборку из пяти списков покупок: {(apple, banana), (apple, banana, cake), (apple, cake, dish), (dish, egg), (dish, egg, fish)}, или сокращённо {ab, abc, acd, de, def}. Каждый список - транзакция. Каждый купленный предмет является объектом. Представим себе, что мы хотим сравнить между собой следующие два разбиения на кластеры:
1: {{ab, abc, acd}, {de, def}}
2: {{ab, abc}, {acd, de, def}}.
Для первого и второго вариантов разбиения в каждом кластере рассчитаем количество вхождений в него каждого элемента транзакции, а затем вычислим ширину W (количество уникальных объектов кластера) и высоту H (отношение общего числа объектов и ширины). Например, кластер {ab, abc, acd} имеет вхождения a:3, b:2, c:2, d:1 с H=2 и W=4.
Лучшим признаётся разбиение, при котором достигается минимум функции [math] Profit(C)=\frac{\sum^{k}_{i=1} H(C_i) \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} [/math] = [math]\frac{\sum^{k}_{i=1} \frac {S(C_i)}{{W(C_i)}^r} \times \mid C_i \mid} {\sum^{k}_{i=1} \mid C_i \mid} [/math] Здесь [math]r[/math] - коэффициент отталкивания, [math]k[/math] - количество кластеров, [math]S(C_i)[/math] - число объектов в кластере [math]C_i[/math], [math]\mid C_i \mid[/math] - число транзакций в кластере [math] C_i [/math], [math]H(C_i)[/math] и [math]W(c_i)[/math] - высота и ширина [math]C_i[/math] соответственно.