Участник:Sveta

Общая схема описания алгоритмов имеет следующий вид:

1 Свойства и структура алгоритмов

Свойства алгоритмов никак не зависят от вычислительных систем, и с этой точки зрения данная часть AlgoWiki имеет безусловную собственную ценность. Описание алгоритма делается один раз, после чего многократно используется для его реализации в различных программно-аппаратных средах. Несмотря на то, что в данной части мы рассматриваем лишь машинно-независимые свойства алгоритмов, соображения, важные на этапе реализации, или же ссылки на соответствующие пункты части II AlgoWiki, здесь также вполне уместны.

1.1 Общее описание алгоритма

Модель дуополии Штакельберга является развитием модели дуополии Курно. Если в модели Курно считается, что участники рынка не прогнозируют отклика конкурента на собственные действия, то в модели Штакельберга один участник рынка не прогнозирует поведения конкурента, а второй учитывает поведение первого, зная, что конкурент не ответит на его действия. Другими словами, второй участник рынка знает, что первый участник рынка ведет себя в соответствии с моделью Курно.

1.2 Математическое описание алгоритма

Есть множество стратегий первого игрока [math] X [/math] и мноожество стратегий [math] Y [/math] второго игрока. Первым ходит игрок, называемый лидером, его стратегия [math] x \in X [/math]. Второй игрок, называемый подчиненным, ходит стратегией [math] y \in Y [/math]. У каждого игрока есть своя функция выигрыша. Для лидера это функция [math] H(x,y) [/math]. Для подчиненного [math] G(x,y) [/math]. Оба хотят максимизировать свой выигрыш, при условии лояльности(лояльность, это когда при условии одинакового выигрыша для второго, он максимизирует выигрыш первого) второго игрока по отношении к первому. Набор стратегий [math] (x^*,y^*) [/math] называется равновесием Штакельберга, если [math] y^* = R(x^*) [/math] есть наилучший ответ подчиненного на стратегию лидера, которая находится как решение задачи [math] H(x^*, y^*) = max H(x,R(x)) [/math]

1.3 Вычислительное ядро алгоритма

Для каждой стратегии первого, найдем множество наилучших ответов второго, благожелательных к первому. По всем найденым ответам второго, максимизируем выигрыш первого.

1.4 Макроструктура алгоритма

Если алгоритм использует в качестве составных частей другие алгоритмы, то это указывается в данном разделе. Если в дальнейшем имеет смысл описывать алгоритм не в максимально детализированном виде (т.е. на уровне арифметических операций), а давать только его макроструктуру, то здесь описывается структура и состав макроопераций. Если в других разделах описания данного алгоритма в рамках AlgoWiki используются введенные здесь макрооперации, то здесь даются пояснения, необходимые для однозначной интерпретации материала. Типичные варианты макроопераций, часто встречающиеся на практике: нахождение суммы элементов вектора, скалярное произведение векторов, умножение матрицы на вектор, решение системы линейных уравнений малого порядка, сортировка, вычисление значения функции в некоторой точке, поиск минимального значения в массиве, транспонирование матрицы, вычисление обратной матрицы и многие другие.

Описание макроструктуры очень полезно на практике. Параллельная структура алгоритмов может быть хорошо видна именно на макроуровне, в то время как максимально детальное отображение всех операций может сильно усложнить картину. Аналогичные аргументы касаются и многих вопросов реализации, и если для алгоритма эффективнее и/или технологичнее оставаться на макроуровне, оформив макровершину, например, в виде отдельной процедуры, то это и нужно отразить в данном разделе. Выбор макроопераций не однозначен, причем, выделяя различные макрооперации, можно делать акценты на различных свойствах алгоритмов. С этой точки зрения, в описании одного алгоритма может быть представлено несколько вариантов его макроструктуры, дающих дополнительную информацию о его структуре. На практике, подобные альтернативные формы представления макроструктуры алгоритма могут оказаться исключительно полезными для его эффективной реализации на различных вычислительных платформах.

1.5 Схема реализации последовательного алгоритма

Здесь описываются все шаги, которые нужно выполнить при последовательной реализации данного алгоритма. В некотором смысле, данный раздел является избыточным, поскольку математическое описание уже содержит всю необходимую информацию. Однако он, несомненно, полезен: схема реализации алгоритма выписывается явно, помогая однозначной интерпретации приводимых далее оценок и свойств.

Описание может быть выполнено в виде блок-схемы, последовательности математических формул, обращений к описанию других алгоритмов, фрагмента кода на Фортране, Си или другом языке программирования, фрагмента кода на псевдокоде и т.п. Главное - это сделать схему реализации последовательного алгоритма полностью понятной. Совершенно не обязательно все шаги детализировать до элементарных операций, отдельные шаги могут соответствовать макрооперациям, отвечающим другим алгоритмам.

Описание схемы реализации вполне может содержать и словесные пояснения, отражающие какие-либо тонкие нюансы самого алгоритма или его реализации. Уже в данном разделе можно сказать про возможный компромисс между объемом требуемой оперативной памяти и временем работы алгоритма, между используемыми структурами данных и степенью доступного параллелизма. В частности, часто возникает ситуация, когда можно ввести дополнительные временные массивы или же отказаться от использования специальных компактных схем хранения данных, увеличивая степень доступного параллелизма.

1.6 Последовательная сложность алгоритма

В данном разделе описания свойств алгоритма приводится оценка его последовательной сложности, т.е. числа операций, которые нужно выполнить при последовательном исполнении алгоритма (в соответствии с п.1.5). Для разных алгоритмов понятие операции, в терминах которой оценивается его сложность, может существенно различаться. Это могут быть операции для работы с вещественными числами, целыми числами, поразрядные операции, обращения в память, обновления элементов массива, элементарные функции, макрооперации и другие. В LU-разложении преобладают арифметические операции над вещественными числами, а для транспонирования матриц важны лишь обращения к памяти: это и должно найти отражение в описании.

Если выбор конкретного типа операций для оценки сложности алгоритма не очевиден, то нужно привести обоснование возможных вариантов. В некоторых случаях можно приводить оценку не всего алгоритма, а лишь его вычислительного ядра: в таком случае это нужно отметить, сославшись на п.1.1.

Например, сложность алгоритма суммирования элементов вектора сдваиванием равна [math]n-1[/math]. Сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки – [math]n\log_2n[/math] операций комплексного сложения и [math](n\log_2n)/2[/math] операций комплексного умножения. Сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это [math]n[/math] вычислений квадратного корня, [math]n(n-1)/2[/math] операций деления, по [math](n^3-n)/6[/math] операций умножения и сложения (вычитания).

1.7 Информационный граф

Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма ). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций .

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

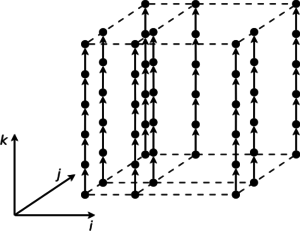
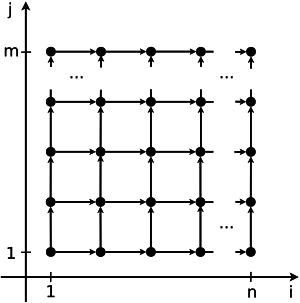
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

1.8 Ресурс параллелизма алгоритма

Здесь приводится оценка параллельной сложности алгоритма: числа шагов, за которое можно выполнить данный алгоритм в предположении доступности неограниченного числа необходимых процессоров (функциональных устройств, вычислительных узлов, ядер и т.п.). Параллельная сложность алгоритма понимается как высота канонической ярусно-параллельной формы . Необходимо указать, в терминах каких операций дается оценка. Необходимо описать сбалансированность параллельных шагов по числу и типу операций, что определяется шириной ярусов канонической ярусно-параллельной формы и составом операций на ярусах.

Параллелизм в алгоритме часто имеет естественную иерархическую структуру. Этот факт очень полезен на практике, и его необходимо отразить в описании. Как правило, подобная иерархическая структура параллелизма хорошо отражается в последовательной реализации алгоритма через циклический профиль результирующей программы (конечно же, с учетом графа вызовов), поэтому циклический профиль (п.1.5) вполне может быть использован и для отражения ресурса параллелизма.

Для описания ресурса параллелизма алгоритма (ресурса параллелизма информационного графа) необходимо указать ключевые параллельные ветви в терминах конечного и массового параллелизма. Далеко не всегда ресурс параллелизма выражается просто, например, через координатный параллелизм или, что то же самое, через независимость итераций некоторых циклов (да-да-да, циклы - это понятие, возникающее лишь на этапе реализации, но здесь все так связано… В данном случае, координатный параллелизм означает, что информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей). С этой точки зрения, не менее важен и ресурс скошенного параллелизма. В отличие от координатного параллелизма, скошенный параллелизм намного сложнее использовать на практике, но знать о нем необходимо, поскольку иногда других вариантов и не остается: нужно оценить потенциал алгоритма, и лишь после этого, взвесив все альтернативы, принимать решение о конкретной параллельной реализации. Хорошей иллюстрацией может служить алгоритм, структура которого показана на рис.2: координатного параллелизма нет, но есть параллелизм скошенный, использование которого снижает сложность алгоритма с [math]n\times m[/math] в последовательном случае до [math](n+m-1)[/math] в параллельном варианте.

Рассмотрим алгоритмы, последовательная сложность которых уже оценивалась в п.1.6. Параллельная сложность алгоритма суммирования элементов вектора сдваиванием равна [math]\log_2n[/math], причем число операций на каждом ярусе убывает с [math]n/2[/math] до [math]1[/math]. Параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки - [math]\log_2n[/math]. Параллельная сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это [math]n[/math] шагов для вычислений квадратного корня, [math](n-1)[/math] шагов для операций деления и [math](n-1)[/math] шагов для операций умножения и сложения.

1.9 Входные и выходные данные алгоритма

Входными данными являются пара матриц [math] H(x,y) [/math], [math] G(x,y) [/math] одинакового размера [math]n * m [/math] (стратегии обоих игроков). Выходные данные это множество пар чисел [math] (x^*,y^*) [/math], где каждая из пар является равновесием по Штакельбергу в нашей дуаполии.

2 Программная реализация алгоритма

Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.

2.1 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

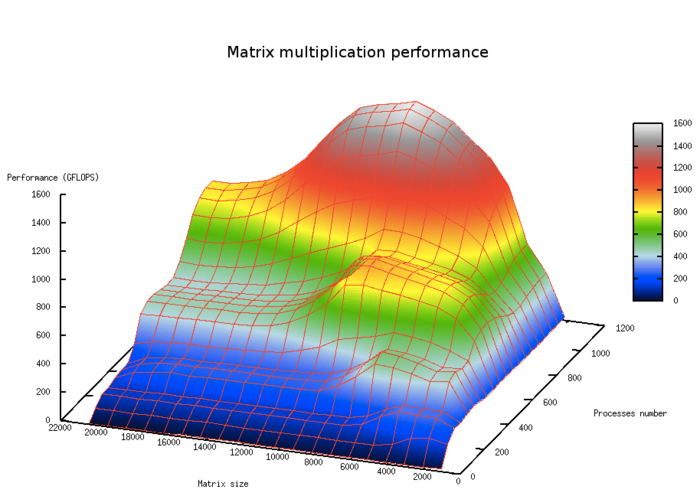
Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи . При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи

2.2 Существующие реализации алгоритма

Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.