Участник:S s serov/DSn-метод решения уравнения переноса

Автор текущей версии статьи: Серов Сергей

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Уравнение переноса нейтронов описывает процессы поглощения, рассеяния и размножения, происходящие в ядерном реакторе. Одним из популярных детерминистических методов его решения, как известно, является DSn-метод . Далее описывается DSn-метод решения стационарного одногруппового уравнения переноса нейтронов в 1D плоско-параллельной геометрии с изотропным рассеянием.

Геометрическая модель решаемой задачи имеет следующий вид: перпендикулярно единственной участвующей в рассмотрении оси $x$ (будем считать, что она направлена слева направо) расположено несколько бесконечных по осям $y$ и $z$ плоско-параллельных слоев некоторого вещества (например, урана, свинца, воды, воздуха и т.д.) заданной толщины, прилегающих друг к другу.

Само уравнение переноса (УП) нейтронов записывается в следующем виде:

$\mu \frac{dN(x,\mu)}{dx} + \sigma(x)N(x,\mu) = Q(x,\mu),$

где

$Q(x,\mu) = \frac{\sigma_S^0(x)}{2}\int_{-1}^1 N(x,\mu')d\mu' + \frac{1}{2}q(x).$

Используемые обозначения:

• $\mu = cos(\theta)$ --- косинус угла $\theta$ между направлением полета нейтрона и положительным направлением оси $x$;
• $N(x,\mu)$ --- плотность потока нейтронов, летящих в заданном направлении $\mu$ в слое с координатой $x$;
• $SN(x) = \int_{-1}^1 N(x,\mu')d\mu'$ --- скалярный поток нейтронов в точке $x$;
• $\sigma(x)$ --- макроскопическое сечение взаимодействия нейтронов со средой в точке $x$, т.е. коэффициент обобщенного поглощения нейтронов физическим материалом, расположенным в этой точке среды;
• $\sigma_S^0(x)$ --- изотропное макроскопическое сечение обобщенного рассеяния нейтронов в точке $x$ среды, т.е. коэффициент обобщенного рассеяния нейтронов в этой точке среды;
• $q(x)$ --- независимый изотропный источник нейтронов в точке $x$.

Одногрупповое УП является интегро-дифференциальным. Левая его часть представляет собой обыкновенный дифференциальный оператор, который отвечает за пролет нейтронов через физическую среду. Правая часть УП содержит интеграл столкновений, который отвечает за рождение вторичных частиц в реакциях упругого и неупругого рассеяния, деления нейтронов, реакций типа $(n,2n)$ и других, а также независимый источник нейтронов. Целью решаемой задачи является нахождение плотности потока нейтронов $N(x,\mu)$ или скалярного потока $SN(x)$. Для решения задачи достаточно вычислить только скалярный поток $SN(x)$, так как дифференциальная плотность потока нейтронов $N(x,\mu)$ может быть получена из решения ОДУ с известной правой частью, в которую входит скалярный поток $SN(x)$. Таким образом, целью расчета является нахождение стационарного (на бесконечности по времени) распределения плотности потока нейтронов $N(x,\mu)$ и скалярного потока $SN(x)$.

Для каждого слоя вещества необходимый набор параметров ($\sigma$ и $\sigma_S^0$), задающих его физические свойства, известен, а также известны краевые условия на левом и правом концах рассматриваемой системы. В рассматриваемой постановке задачи мы считаем, что правее $x_{max}$ находится вакуум, то есть плотность потока нейтронов равна нулю по всем направлениям полета нейтронов, влетающих справа налево через правую границу системы: $N(x_{max},\mu) = 0, \forall \mu \in [-1, 0]$; а на левой границе $x_{min}$ заданы краевые условия зеркального отражения, при котором нейтроны, прилетевшие справа на левую границу, отражаются от нее, изменяя направление своего полета с $\mu$ на $-\mu$, то есть краевое условие имеет вид: $N(x_{min},-\mu) = N(x_{min},\mu), \forall \mu \in [-1, 0]$. Также значения параметров $\sigma(x), \sigma_S^0(x)$ и $q(x)$ будем считать постоянными в каждом из слоев. Слой с одинаковыми макросечениями и независимым источником нейтронов будем также называть областью.

Для численного решения задачи вводятся 2 одномерные дискретные сетки: по оси $x$ и по косинусу угла $\mu$.

Поэтому данный метод решения УП нейтронов и получил название метода дискретных ординат (по $\mu$ на плоскости $(x,\mu)$), или DSn – метода.

Альтернативными методами решения этого уравнения являются метод характеристик, метод Монте-Карло и некоторые другие.

1.2 Математическое описание алгоритма

Входные данные:

• геометрическая модель задачи (количество слоев, их расположение на оси $x$ и толщина);
• $\sigma(x)$ для каждого слоя;
• $\sigma_S^0(x)$ для каждого слоя;
• $q(x)$ для каждого слоя.

Параметры:

• $I$ --- количество ячеек дискретной сетки по оси $x$;
• $M$ --- количество ячеек дискретной сетки по параметру $\mu$;
• $\nu_0$ --- количество итераций по правой части УП.

Выходные данные:

• $SN(x)$ для каждой ячейки введенной сетки.

Введем дискретную сетку по $x$ и по $\mu$:

$\mathbb{X} = \{x_i, i \in \{1, \dots, I + 1\} | x_{i+1} = x_i + \Delta x, x_1 = x_{min}, \Delta x = \frac{x_{max} - x_{min}}{I}\},$

$\mathbb{M} = \{\mu_m, m \in \{1, \dots, M + 1\} | \mu_{m+1} = \mu_m + \Delta \mu, \mu_1 = -1, \Delta \mu = \frac{2}{M}\}.$

Середины ячеек соответствующих сеток будем обозначать как $x_{i+1/2}$ и $\mu_{m+1/2}$.

Алгоритм решения задачи выглядит так:

1. Задается некоторое начальное неотрицательное распределение нейтронов в системе $SN_{i+1/2}$.
2. Для решения интегро-дифференциального УП нейтронов используем метод итераций источника, то есть организуем итерации $\nu$ по правой части УП, которая называется источником (он является суммой интеграла столкновений и независимого источника нейтронов). Независимый источник $q_{i+1/2}$ от номера итерации не зависит и является постоянным на всех итерациях. Интеграл столкновений $SN_{i+1/2}$ нужно перевычислять на каждой итерации. Более конкретно, по уже известному с предыдущей итерации или из краевого условия распределению $SN_{i+1/2}$ вычисляем правую часть УП, то есть $Q_{i+1/2}$ для всех $i \in \{1, \dots, I\}$. Далее задача сводится к решению ОДУ на каждой итерации по правой части УП.
3. Алгоритм решения ОДУ на каждой итерации по правой части является неоднородным. Сначала рассчитываются все направления полета нейтронов с отрицательными $\mu$. При этом на правой границе системы задаются вакуумные краевые условия, то есть $N(x_{max},\mu)=0$ для всех $\mu \lt 0$. Расчет по $x$ ведется справа налево, то есть по убыванию индекса $i+1/2$. На левой границе системы $x_{min}$ формируются краевые условия отражения $N_{Left}(\mu_{m+1/2})$ (для всех $\mu \lt 0$). Далее они будут использоваться как краевые условия на левой границе системы $x_{min}$ при расчете всех направлений $\mu \gt 0$.
4. Рассчитываем все направления $\mu_{m+1/2} \gt 0$. При этом порядок расчета по координате $x$ будет следующим: от левой границы системы $x_{min}$ к правой $x_{max}$, то есть по возрастанию индекса $i+1/2$. Чтобы "оттолкнуться" от левой границы $x_{min}$ используем уже сформированные при расчете случая $\mu \lt 0$ краевые условия $N_{Left}(\mu_{m+1/2})$ на левой границе системы. Продолжаем для случая $\mu \gt 0$ накапливать массив $SN_{i+1/2}^{new}$. В конце расчета всех $\mu_{m+1/2}$ в массиве $SN_{i+1/2}^{new}$ уже насчитаны новые значения $SN$ для следующей итерации $\nu$. Их нужно только присвоить в нужном месте программы снова в массив $SN_{i+1/2}$.
5. Теперь опишем метод решения обыкновенного дифференциального уравнения с известной правой частью и используемые для этого разностные схемы. Также учитываем, что в указанной постановке задачи параметры $\sigma(x), \sigma_S^0(x)$ и $q(x)$ заданы постоянными для каждого слоя.

   Уравнение имеет вид:

    :$\mu_{m+1/2} \frac{dN(x,\mu_{m+1/2})}{dx} + \sigma(x)N(x,\mu_{m+1/2}) = Q(x,\mu_{m+1/2}).$

   Проинтегрируем его по ячейке $T_{i+1/2} = [x_i, x_{i+1}]$ и получим уравнение баланса нейтронов (сечение взаимодействия нейтронов со средой $\sigma(x) = Const$ в каждой области вещества и может быть вынесено за знак интеграла):

    :$\mu_{m+1/2}(N_{i+1} - N_i) + \sigma(x) \int_{x_i}^{x_{i+1}} N(x,\mu_{m+1/2})dx = \int_{x_i}^{x_{i+1}} Q(x,\mu_{m+1/2})dx.$

   Далее по теореме о среднем:

    :$\int_{x_i}^{x_{i+1}} N(x,\mu_{m+1/2})dx = \bar{N}\cdot \Delta x, \int_{x_i}^{x_{i+1}} Q(x,\mu_{m+1/2})dx = \bar{Q}\cdot \Delta x, \Delta x = x_{i+1} - x_i.$

   Тогда уравнение (называемое уравнением баланса) примет вид:

    :$\mu_{m+1/2}(N_{i+1} - N_i) + \sigma \bar{N} \Delta x = \bar{Q} \Delta x.$

6. При решении УП нейтронов на основе традиционного DSn-метода обычно используются 2 основные конечно-разностные схемы: DD (diamond difference) – алмазная и St (step) – шаговая. Приведем далее формулы, соответствующие случаю расчета всех направлений полета нейтронов с положительными $\mu$. Напомним, что в этом случае расчет по координате $x$ ведется по возрастанию индекса $i+1/2$. Для случая $\mu \lt 0$ формулы для DD– и St– схем выводятся аналогично.

   St-схема (шаговая) ($\bar{N} = N_{i+1})$:

    :$\bar{N} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}, N_{i+1} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}.$

   DD-схема (алмазная) ($\bar{N} = \frac{1}{2}(N_i + N_{i+1}), N_{i+1} = 2\bar{N} - N_i$):

    :$\bar{N} = \frac{\bar{Q} \Delta x + 2\mu_{m+1/2} N_i}{\sigma \Delta x + 2\mu_{m+1/2}}, N_{i+1} = \frac{2\bar{Q} \Delta x + (2\mu_{m+1/2} - \sigma \Delta x) N_i}{\sigma \Delta x + 2\mu_{m+1/2}}.$

   Алмазная DD-схема имеет 2-ой порядок аппроксимации и поэтому является более точной, чем St-схема 1-го порядка аппроксимации, однако не обладает свойствами положительности и монотонности, в отличие от последней, вследствие чего в некоторых случаях может давать отрицательные значения плотности потока, что недопустимо с точки зрения физики явления (невозможно в реальной физической ситуации). В связи с этим традиционный DSn–метод использует обе конечно-разностные схемы для обеспечения, с одной стороны, максимальной точности разностного решения, а с другой – гарантированной его неотрицательности, то есть физичности.

   Переключающий критерий устроен следующим образом: если использование алмазной DD-схемы в какой либо ячейке сетки приводит к отрицательным значениям плотности потока внутри ячейки или на выходе из нее, то расчет этой же ячейки сетки проводится на основе использования шаговой St-схемы, гарантирующей неотрицательность сеточного решения.

В случае использования подробных дискретных сеток время работы приведенного алгоритма может быть достаточно большим. В этом случае актуальной задачей является распараллеливание этого алгоритма.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из вычисления значений плотности потока нейтронов в каждой ячейке сетки по оси $x$ для каждого значения косинуса направления полета нейтронов в соответствии с выбранными разностными схемами.

1.4 Макроструктура алгоритма

Как и записано в описании ядра алгоритма, основную часть составляет решение обыкновенного дифференциального уравнения с помощью алмазной и шаговой (при необходимости) разностных схем.

1.5 Схема реализации последовательного алгоритма

1. Задать неотрицательное распределение скалярного потока нейтронов $SN$ в системе.
2. На каждой итерации:
   1. Вычислить правую часть УП для каждой ячейки двумерной сетки по $x$ и $\mu$: $Q(x,\mu) = \frac{\sigma_S^0(x)}{2}\int_{-1}^1 N(x,\mu')d\mu' + \frac{1}{2}q(x)$.
   2. Провести вычисление плотностей потока нейтронов в каждой ячейке двумерной сетки справа налево по оси $x$ с использованием алмазной и шаговой (при необходимости) разностных схем:

      St-схема (шаговая) ($\bar{N} = N_{i+1})$:

       :$\bar{N} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}, N_{i+1} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}.$

      DD-схема (алмазная) ($\bar{N} = \frac{1}{2}(N_i + N_{i+1}), N_{i+1} = 2\bar{N} - N_i$):

       :$\bar{N} = \frac{\bar{Q} \Delta x + 2\mu_{m+1/2} N_i}{\sigma \Delta x + 2\mu_{m+1/2}}, N_{i+1} = \frac{2\bar{Q} \Delta x + (2\mu_{m+1/2} - \sigma \Delta x) N_i}{\sigma \Delta x + 2\mu_{m+1/2}}.$

   3. Вычислить скалярный поток нейтронов в каждой ячейке сетки по $x$ путем интегрирования плотностей потока нейтронов по всем значениям косинуса угла полета $\mu$: $SN(x) = \int_{-1}^1 N(x,\mu')d\mu'$.

1.6 Последовательная сложность алгоритма

Умножения и сложения (вычитания) составляют основную часть алгоритма.

Для решения уравнения переноса DSn-методом на каждой итерации требуется:

$O(I*M)$ умножений и сложений.

Таким образом, последовательная сложность всего алгоритма составляет:

$O(\nu_0*I*M)$ умножений и сложений.

При классификации по последовательной сложности, таким образом, DSn-метод решения УП относится к алгоритмам с линейной сложностью.

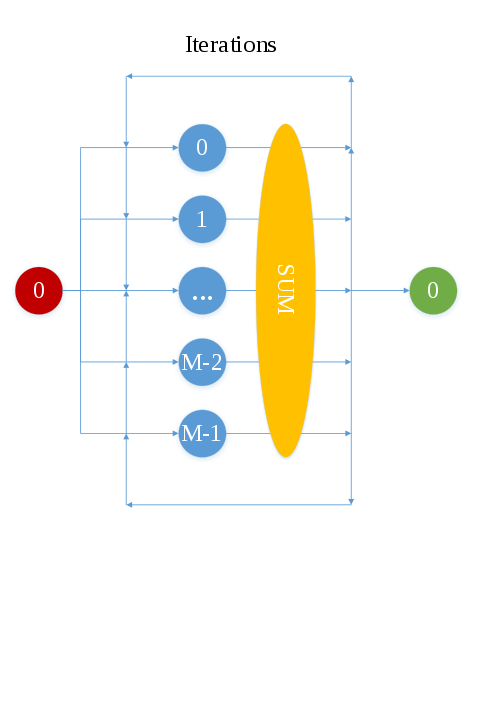
1.7 Информационный граф

Красным цветом обозначена вершина процесса, считывающего данные, формирующего массивы исходных данных и рассылающего их всем остальным запущенным процессам, число которых меньше либо равно числу ячеек введенной сетки по $\mu$.

Синим цветом обозначены вершины всех процессов, которые для определенных ячеек сетки по $\mu$ на каждой итерации вычисляют сначала правую часть УП, а затем с помощью разностных схем --- значения плотности потока нейтронов во всех ячейках оси $x$.

Желтым цветом обозначена вершина, отвечающая операции суммирования значений, насчитанных каждым процессом, и их рассылки всем участвующим в вычислениях процессам.

Зеленым цветом обозначена вершина процесса, который, после завершения процессами выполнения всех итераций, собирает окончательные значения скалярного потока нейтронов в одном массиве и выводит результат работы.

1.8 Ресурс параллелизма алгоритма

Имея в распоряжении $M$ процессов, мы имеем возможность производить вычисления плотности потоков нейтронов в ячейках сетки по оси $x$ для разных значений косинуса угла полета $\mu$ независимо друг от друга. Это означает, что каждый процесс по отдельности может вычислять правую часть уравнения переноса, а затем и решать его с использованием разностных схем для некоторых выделенных ему значений параметра $\mu$, а лишь затем, в конце итерации, обмениваться вычисленными значениями с другими процессами для пересчета правой части уравнения.

Таким образом, сложность параллельной реализации будет составлять

$O(\nu_0*I)$ умножений и сложений.

1.9 Входные и выходные данные алгоритма

Входные данные: массив $\sigma(x)$ для каждого слоя, массив $\sigma_S^0(x)$ для каждого слоя, массив $q(x)$ для каждого слоя.

Объем входных данных: $3k$, где $k$ --- количество слоев в геометрии задачи.

Выходные данные: массив $SN(x)$ для каждой ячейки введенной сетки.

Объем выходных данных: $N$, где $N$ --- количество ячеек введенной сетки по $x$.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

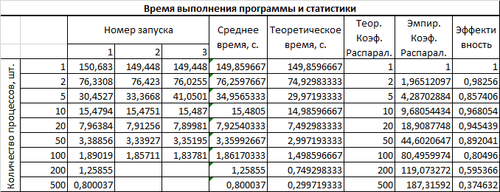
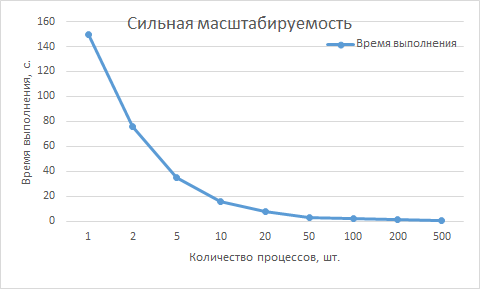
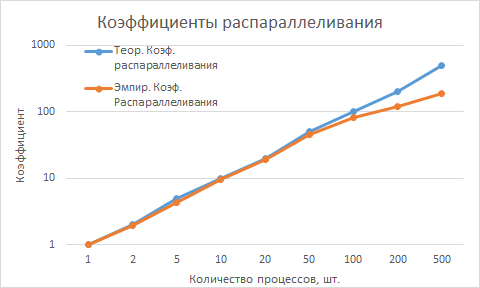
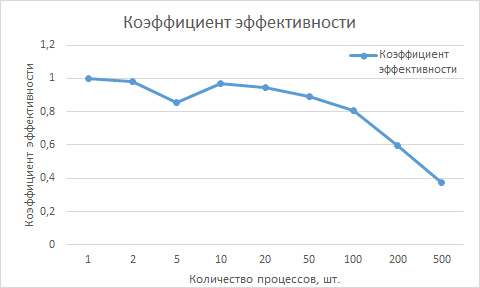
Приведем результаты запусков параллельной реализации DSn-метода решения УП для на суперкомпьютере "Ломоносов" для разного числа процессов. Использованные параметры: число ячеек сетки по оси $x$: $I = 80000$, число ячеек сетки по оси $\mu$: $M = 1000$, количество итераций метод $\nu_0 = 50$.

В прикрепленной таблице содержатся времена выполнения программы для разного числа запущенных процессов. В следующих столбцах указаны среднее время по 3-м запускам (для 200 и 500 процессов --- по 1-му), теоретическое время работы программы (рассчитанное как отношение времени работы на одном процессе к количеству параллельных процессов), теоретический и эмпирический коэффициенты распараллеливания (рассчитанные как отношение теоретического и эмпирического времени работы на нескольких процессах ко времени работы на одном процессе) и коэффициент эффективности (рассчитанный как отношение эмпирического коэффициента распараллеливания к теоретическому).

2.4.2 Характеристики программно-аппаратной среды

Все вычисления были произведены на суперкомпьютере "Ломоносов".

Для компиляции был использован компилятор языка C++ GNU 4.4.6, реализация MPI: Intel MPI 4.0.3.

Вычисления производились в сегментах test, regular4 и regular6. Ограничений на время выполнения программы наложено не было.

3 Литература

<references \>