Участник:Konstantin 013

Основные авторы описания: К.В.Телегин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм находит равновесия Нэша в игре двух лиц с конечным числом стратегий

1.2 Математическое описание алгоритма

Определим игру двух лиц. Пусть первый игрок имеет в своём распоряжении стратегии [math] x [/math] из множества стратегий [math] X [/math], а второй игрок стратегии [math] y [/math] из множества стратегий [math] Y [/math]. Будем рассматривать игру в нормальной форме. Это означает, что каждый из игроков выбирает стратегию, не зная выбора партнёра. Пару стратегий [math] (x, y) [/math] будем называть ситуацией. У первого игрока имеется функция выигрыша [math] F(x, y) [/math], а у второго [math] G(x, y) [/math], определённые на на множестве всех ситуаций [math] X × Y [/math]. каждый игрок стремится, по возможности, максимизировать свою функцию выигрыша. Таким образом, игра двух лиц в нормальной форме задаётся набором [math] \Gamma \langle X, Y, F(x, y), G(x, y) \rangle [/math]. Ситуация [math] (x^0, y^0) [/math] называется равновесием по Нэшу игры [math] \Gamma [/math] если: [math] \max_{x \in X} F(x, y^0) = F(x^0, y^0) \quad , \quad \max_{y \in Y} G(x^0, y) = G(x^0, y^0) [/math]

Иными словами, каждому из игроков невыгодно отколняться от ситуации равновесия.

В данной статье мы рассмотрим нахождение ситуаций равновесий Нэша в одном специальном случае для множеств [math] X, Y [/math]. Назовём игру [math] \Gamma [/math] биматричной, если [math] X, Y [/math] - конечные множества. тогда можно считать, что [math] X = [1, ..., n], Y = [1, ..., m] [/math], а [math] F, G [/math] - являются матрицами [math] R^{n × m} [/math]

1.3 Вычислительное ядро алгоритма

Сначала будет естественно для каждого столбца матрицы [math] F [/math] найти максимум в нём (таким образом мы находим наилучший ответ 1-го игрока, при фиксированной стратегии 2-го) и для каждой строки матрицы [math] G [/math] найти максимум в ней (ищем наилучшие ответы 2-го игрока). Т.е. мы ищем для каждого из [math] m [/math] векторов [math] R^n [/math] мы ищем максимум и для каждого из [math] n [/math] векторов [math] R^m [/math] мы ищем максимум. После этого для каждой ситуации [math] (x^0, y^0) [/math] несложно понять, является ли она равновесием Нэша: нужно просто проверить, что [math] F(x^0, y^0) [/math] - максимальный элемент в [math] y^0 [/math]-м столбце матрицы [math] F [/math] и [math] G(x^0, y^0) [/math] - максимальный элемент в [math] x^0 [/math]-ой строке матрицы [math] G [/math].

1.4 Макроструктура алгоритма

Алгоритм в качестве подзадачи многократно использует поис максимума в массиве (n раз для массиве длины m и ь раз для массиве длины n). Затем, для все возможных позиций проверяется, является она равноесием по нэшу, как это описывалось в разделе выше.

1.5 Схема реализации последовательного алгоритма

Данный код реализует последовательную версию алгоритма

#include <vector>
#include <algorithm>
#include <list>
#include <utility>


std::list<std::pair<int, int> > 
nash_equilibrium(
	const std::vector<std::vector<double> > &f,
	const std::vector<std::vector<double> > &g)
{
	std::list<std::pair<int, int> > res;

	int n = f.size();
	int m = g[0].size();

	std::vector<double> maxf(m);
	for (int i = 0; i < m; ++i) {
		maxf[i] = f[0][i];
		for (int j = 1; j < n; ++j) {
			maxf[i] = std::max(maxf[i], f[j][i]);
		}
	}

	std::vector<double> maxg(n);
	for (int i = 0; i < n; ++i) {
		maxg[i] = g[i][0];
		for (int j = 1; j < m; ++j) {
			maxg[i] = std::max(maxg[i], g[i][j]);
		}
	}


	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (f[i][j] == maxf[j] && g[i][j] == maxg[i]) {
				res.emplace_back(i, j);
			}
		}
	}

	return res;
}

1.6 Последовательная сложность алгоритма

Сложность поиска максима во всех строках(стоблцах) в этих матрицах составит [math] O(nm) [/math]. после этого проверка каждого элемента на равновесие имеет сложность [math] O(1) [/math], а всех соответственно [math] O(nm) [/math].

1.7 Информационный граф

Для начала был создан граф поиска максимума для каждого столбца матрицы F. поиск максимума для каждой строки матрицы G делается аналогично.

Рис.1. поиск максимума для каждого столбца матрицы F

1.8 Ресурс параллелизма алгоритма

Для нахождения максимума в каждой из [math] n [/math] строк матрицы [math] F [/math] понадобится [math] m - 1 [/math] операция сравнения для вещественных чисел. Аналогично, для нахождения максимума в каждом из [math] m [/math] столбцов матрицы [math] G [/math] понадобится [math] n - 1 [/math] операция сравнения для вещественных чисел. Далее, для определения каждой ситуации на равновесие нужно просто сравнить значение в [math] F [/math] с максимумом в столбце и в [math] G [/math] с максимумом в строке, т.е. для каждой ситуации это [math] O(1) [/math], а так как, для каждой ситуации это независимые действия, при неограниченном числе ресурсов все вычисления имеют сложность [math] O(1) [/math].

1.9 Входные и выходные данные алгоритма

Входные данные: две матрицы [math] R^{n × m} [/math]

Выходные данные: список пар [math] (i, j) [/math], где [math] i \in [1 .. n], j \in [1 .. m] [/math]

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Здесь описываются особенности и варианты реализации алгоритма в виде последовательной программы, которые влияют на эффективность ее выполнения. В частности, в данном разделе имеет смысл сказать о существовании блочных вариантов реализации алгоритма, дополнительно описав потенциальные преимущества или недостатки, сопровождающие такую реализацию. Важный вопрос - это возможные варианты организации работы с данными, варианты структур данных, наборов временных массивов и другие подобные вопросы. Для различных вариантов реализации следует оценить доступный ресурс параллелизма и объем требуемой памяти.

Важным нюансом является описание необходимой разрядности выполнения операций алгоритма (точности). На практике часто нет никакой необходимости выполнять все арифметические операции над вещественными числами с двойной точностью, т.к. это не влияет ни на устойчивость алгоритма, ни на точность получаемого результата. В таком случае, если значительную часть операций можно выполнять над типом float, и лишь в некоторых фрагментах необходим переход к типу double, это обязательно нужно отметить. Это прямое указание не только на правильную реализацию с точки зрения устойчивости по отношению к ошибкам округления, но и на более эффективную.

Опираясь на информацию из п.1.8 (описание ресурса параллелизма алгоритма), при описании последовательной версии стоит сказать про возможности эквивалентного преобразования программ, реализующих данных алгоритм. В дальнейшем, это даст возможность простого использования доступного параллелизма или же просто покажет, как использовать присущий алгоритму параллелизм на практике. Например, параллелизм на уровне итераций самого внутреннего цикла обычно используется для векторизации. Однако, в некоторых случаях этот параллелизм можно поднять "вверх" по структуре вложенности объемлющих циклов, что делает возможной и эффективную реализацию данного алгоритма на многоядерных SMP-компьютерах.

С этой же точки зрения, в данном разделе весьма полезны соображения по реализации алгоритма на различных параллельных вычислительных платформах. Высокопроизводительные кластеры, многоядерные узлы, возможности для векторизации или использования ускорителей - особенности этих архитектур не только опираются на разные свойства алгоритмов, но и по-разному должны быть выражены в программах, что также желательно описать в данном разделе.

2.2 Локальность данных и вычислений

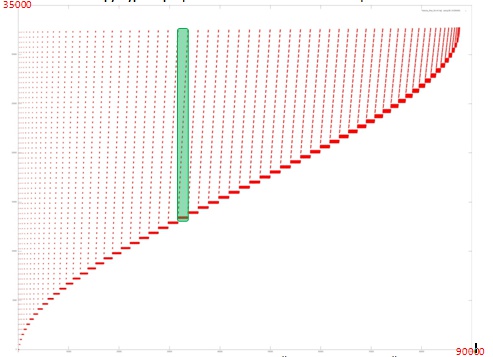
Вопросы локальности данных и вычислений не часто изучаются на практике, но именно локальность определяет эффективность выполнения программ на современных вычислительных платформах . В данном разделе приводятся оценки степени локальности данных и вычислений в программе, причем рассматривается как временна́я, так и пространственная локальность. Отмечаются позитивные и негативные факты, связанные с локальностью, какие ситуации и при каких условиях могут возникать. Исследуется, как меняется локальность при переходе от последовательной реализации к параллельной. Выделяются ключевые шаблоны взаимодействия программы, реализующей описываемый алгоритм, с памятью. Отмечается возможная взаимосвязь между используемыми конструкциями языков программирования и степенью локальности, которыми обладают результирующие программы.

Отдельно приводятся профили взаимодействия с памятью для вычислительных ядер и ключевых фрагментов. Если из-за большого числа обращений по общему профилю сложно понять реальную специфику взаимодействия программ с памятью, то проводится последовательная детализация и приводится серия профилей более мелкого масштаба.

На рис.3 и рис.4 показаны профили обращения в память для программ, реализующих разложение Холецкого и быстрое преобразование Фурье, по которым хорошо видна разница свойств локальности у данных алгоритмов.

Рис.3 Реализация метода Холецкого. Общий профиль обращений в память

Рис.4 Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память

2.3 Возможные способы и особенности параллельной реализации алгоритма

Раздел довольно обширный, в котором должны быть описаны основные факты и положения, формирующие параллельную программу. К их числу можно отнести:

• представленный иерархически ресурс параллелизма, опирающийся на структуру циклических конструкций и на граф вызовов программы;
• комбинацию (иерархию) массового параллелизма и параллелизма конечного;
• возможные способы распределения операций между процессами/нитями;
• возможные способы распределения данных;
• оценку количества операций, объёма и числа пересылок данных (как общего числа, так и в пересчёте на каждый параллельный процесс);

и другие.

В этом же разделе должны быть даны рекомендации или сделаны комментарии относительно реализации алгоритма с помощью различных технологий параллельного программирования: MPI, OpenMP, CUDA или использования директив векторизации.

2.4 Масштабируемость алгоритма и его реализации

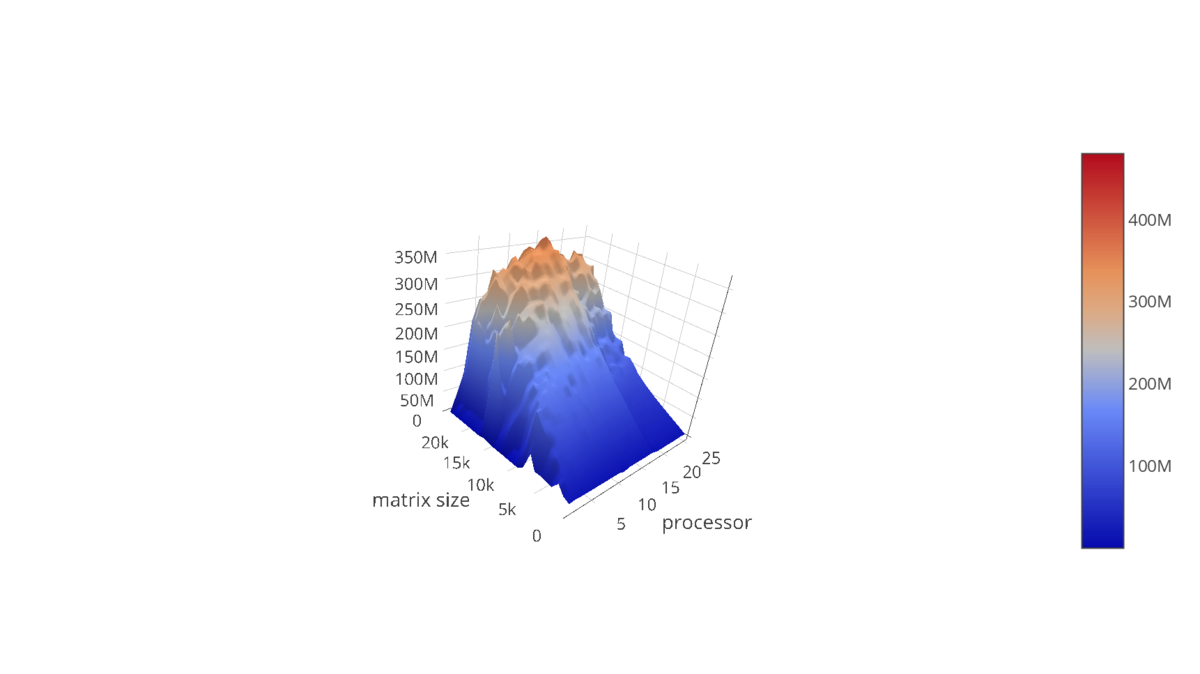
на графике показана зависимость производительности от размеров матриц (в тестах они задавались квадратными) и от числа процессоров. диапазоны:

число процессоров: [1, 32]

сторона матриц: числа от 100 до 24100 с шагом 1000

Рис.1. brr F

2.5 Динамические характеристики и эффективность реализации алгоритма

Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода , предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и эффективность распараллеливания программы, это и эффективность реализации программ по отношению к пиковым показателям работы вычислительных систем.

Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.

2.6 Выводы для классов архитектур

В данный раздел должны быть включены рекомендации по реализации алгоритма для разных классов архитектур. Если архитектура какого-либо компьютера или платформы обладает специфическими особенностями, влияющими на эффективность реализации, то это здесь нужно отметить.

На практике это сделать можно по-разному: либо все свести в один текущий раздел, либо же соответствующие факты сразу включать в предшествующие разделы, где они обсуждаются и необходимы по смыслу. В некоторых случаях, имеет смысл делать отдельные варианты всей части II AlgoWiki применительно к отдельным классам архитектур, оставляя общей машинно-независимую часть I. В любом случае, важно указать и позитивные, и негативные факты по отношению к конкретным классам. Можно говорить о возможных вариантах оптимизации или даже о "трюках" в написании программ, ориентированных на целевые классы архитектур.

2.7 Существующие реализации алгоритма

Данный код реализует параллельную версию алгоритма

#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
#include <mpi.h>


using namespace std;


vector<vector<double> >
create_local_matrix(
	int n, 
	int m,
	int n_proc,
	int rank)
{
	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	vector<vector<double> > F(loc_n, vector<double>(m));
	for (auto &i: F) {
		for (auto &j: i) {
			j = rand() % 1000;
		}
	}	

	return F;
}

vector<double> 
calc_max_in_rows(const vector<vector<double> > &G)
{
	vector<double> G_max(G.size());
	for (int i = 0; i < G.size(); ++i) {
		G_max[i] = G[i][0];
		for (int j = 1; j < G[i].size(); ++j) {
			G_max[i] = max(G_max[i], G[i][j]);
		}
	}

	return G_max;
}

vector<double>
calc_max_in_cols(const vector<vector<double> > &F)
{
	vector<double> F_max(F[0].size());

	for (int i = 0; i < F_max.size(); ++i) {
		F_max[i] = F[0][i];
		for (int j = 1; j < F.size(); ++j) {
			F_max[i] = max(F_max[i], F[j][i]);
		}
	}
	return F_max;
}



int
main(int argc, char *argv[])
{
	int n_proc;
	int rank;
	int n, m;



	MPI_Init(&argc, &argv);
	MPI_Comm_size(MPI_COMM_WORLD, &n_proc);
	MPI_Comm_rank(MPI_COMM_WORLD, &rank);



//reading and sending n and m;
	if (rank == 0) {
		// this is main process
		cin >> n >> m;
		if (n < m) {
			swap(n, m);
		}
	}

	MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
	MPI_Bcast(&m, 1, MPI_INT, 0, MPI_COMM_WORLD);

//Create and fill its part of matrices F and G
	srand(time(NULL));
	vector<vector<double> > F = create_local_matrix(n, m, n_proc, rank);
	vector<vector<double> > G = create_local_matrix(n, m, n_proc, rank);

//every process calculate max in every its rows of matrix G and columns of matrix F

	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	//columns of F
	vector<double> loc_F_col_max = calc_max_in_cols(F);

	//and rows of G
	vector<double> loc_G_row_max = calc_max_in_rows(G);


//now we gather this local maximums in on common vector

	vector<double> F_max(m);
	MPI_Allreduce(loc_F_col_max.data(), F_max.data(), m, MPI_DOUBLE, MPI_MAX, MPI_COMM_WORLD);

//find nash equilibriums

	vector<pair<int, int> > loc_ans;

	for (int i = 0; i < loc_n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (F[i][j] == F_max[j] && G[i][j] == loc_G_row_max[i]) {
				loc_ans.push_back(make_pair(i, j));
			}
		}
	}


	MPI_Finalize();

}