Участник:Konstantin 013

Основные авторы описания: К.В.Телегин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Данный алгоритм находит равновесия Нэша в игре двух лиц с конечным числом стратегий

1.2 Математическое описание алгоритма

Определим игру двух лиц. Пусть первый игрок имеет в своём распоряжении стратегии $x$ из множества стратегий $X$, а второй игрок стратегии $y$ из множества стратегий $Y$. Будем рассматривать игру в нормальной форме. Это означает, что каждый из игроков выбирает стратегию, не зная выбора партнёра. Пару стратегий $(x, y)$ будем называть ситуацией. У первого игрока имеется функция выигрыша $F(x, y)$, а у второго $G(x, y)$, определённые на на множестве всех ситуаций $X × Y$. каждый игрок стремится, по возможности, максимизировать свою функцию выигрыша. Таким образом, игра двух лиц в нормальной форме задаётся набором $\Gamma \langle X, Y, F(x, y), G(x, y) \rangle$. Ситуация $(x^0, y^0)$ называется равновесием по Нэшу игры $\Gamma$ если: $\max_{x \in X} F(x, y^0) = F(x^0, y^0) \quad , \quad \max_{y \in Y} G(x^0, y) = G(x^0, y^0)$

Иными словами, каждому из игроков невыгодно отколняться от ситуации равновесия.

В данной статье мы рассмотрим нахождение ситуаций равновесий Нэша в одном специальном случае для множеств $X, Y$. Назовём игру $\Gamma$ биматричной, если $X, Y$ - конечные множества. тогда можно считать, что $X = [1, ..., n], Y = [1, ..., m]$, а $F, G$ - являются матрицами $R^{n × m}$

1.3 Вычислительное ядро алгоритма

Сначала будет естественно для каждого столбца матрицы $F$ найти максимум в нём (таким образом мы находим наилучший ответ 1-го игрока, при фиксированной стратегии 2-го) и для каждой строки матрицы $G$ найти максимум в ней (ищем наилучшие ответы 2-го игрока). Т.е. мы ищем для каждого из $m$ векторов $R^n$ мы ищем максимум и для каждого из $n$ векторов $R^m$ мы ищем максимум. После этого для каждой ситуации $(x^0, y^0)$ несложно понять, является ли она равновесием Нэша: нужно просто проверить, что $F(x^0, y^0)$ - максимальный элемент в $y^0$-м столбце матрицы $F$ и $G(x^0, y^0)$ - максимальный элемент в $x^0$-ой строке матрицы $G$.

1.4 Макроструктура алгоритма

Алгоритм в качестве подзадачи многократно использует поис максимума в массиве ($n$ раз в массиве длины $m$ и $m$ раз в массиве длины $n$). Затем, для все возможных позиций проверяется, является она равноесием по нэшу, как это описывалось в разделе выше.

1.5 Схема реализации последовательного алгоритма

Данный код реализует последовательную версию алгоритма

#include <vector>
#include <algorithm>
#include <list>
#include <utility>


std::list<std::pair<int, int> > 
nash_equilibrium(
	const std::vector<std::vector<double> > &f,
	const std::vector<std::vector<double> > &g)
{
	std::list<std::pair<int, int> > res;

	int n = f.size();
	int m = g[0].size();

	std::vector<double> maxf(m);
	for (int i = 0; i < m; ++i) {
		maxf[i] = f[0][i];
		for (int j = 1; j < n; ++j) {
			maxf[i] = std::max(maxf[i], f[j][i]);
		}
	}

	std::vector<double> maxg(n);
	for (int i = 0; i < n; ++i) {
		maxg[i] = g[i][0];
		for (int j = 1; j < m; ++j) {
			maxg[i] = std::max(maxg[i], g[i][j]);
		}
	}


	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (f[i][j] == maxf[j] && g[i][j] == maxg[i]) {
				res.emplace_back(i, j);
			}
		}
	}

	return res;
}

1.6 Последовательная сложность алгоритма

Сложность поиска максима во всех строках(стоблцах) в этих матрицах составит $O(nm)$. после этого проверка каждого элемента на равновесие имеет сложность $O(1)$, а всех соответственно $O(nm)$.

1.7 Информационный граф

Для начала был создан граф поиска максимума для каждого столбца матрицы F. поиск максимума для каждой строки матрицы G делается аналогично.

Рис.1. поиск максимума для каждого столбца матрицы F

1.8 Ресурс параллелизма алгоритма

Для нахождения максимума в каждой из $n$ строк матрицы $F$ понадобится $m - 1$ операция сравнения для вещественных чисел. Аналогично, для нахождения максимума в каждом из $m$ столбцов матрицы $G$ понадобится $n - 1$ операция сравнения для вещественных чисел. при неограниченном числе ресурсов, все строки столбцы обрабатываются отдельно, поэтому сложность будет $max(m, n)$. Далее, для определения каждой ситуации на равновесие нужно просто сравнить значение в $F$ с максимумом в столбце и в $G$ с максимумом в строке, т.е. для каждой ситуации это $O(1)$, а так как, для каждой ситуации это независимые действия, при неограниченном числе ресурсов все вычисления имеют сложность $O(1)$.

1.9 Входные и выходные данные алгоритма

Входные данные: две матрицы $R^{n × m}$

Выходные данные: список пар $(i, j)$, где $i \in [1 .. n], j \in [1 .. m]$

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

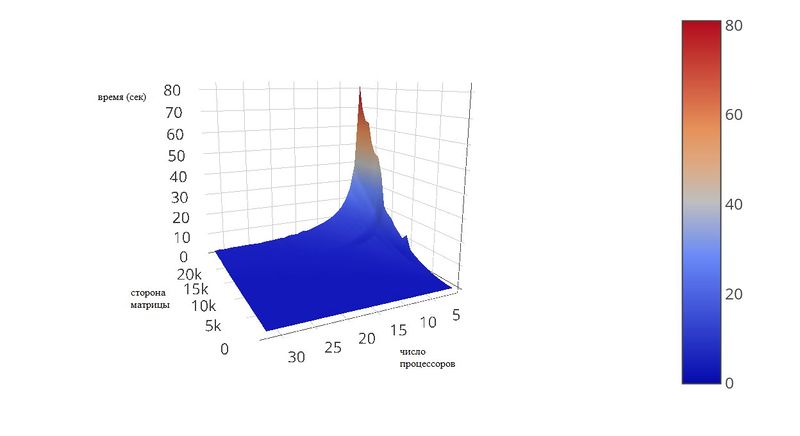
на графике показана зависимость времени работы программы от размеров матриц (в тестах они задавались квадратными) и от числа процессоров. диапазоны:

число процессоров: [1, 32]

сторона матриц: числа от 100 до 24100 с шагом 1000

Рис.1. график зависимости времени работы программы от числа процессоров и стороны матрицы

На графике видно, что в данных тестах процессы нагружаются оптимально, т.к. их увеличение приводит к сильному уменьшению времени. при данных параметрах можно считать, что время ~ $1 / proc_num$, где $proc_num$ - число процессов.

2.7 Существующие реализации алгоритма

Данный код реализует параллельную версию алгоритма

#include <iostream>
#include <vector>
#include <list>
#include <algorithm>
#include <mpi.h>


using namespace std;


vector<vector<double> >
create_local_matrix(
	int n, 
	int m,
	int n_proc,
	int rank)
{
	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	vector<vector<double> > F(loc_n, vector<double>(m));
	for (auto &i: F) {
		for (auto &j: i) {
			j = rand() % 1000;
		}
	}	

	return F;
}

vector<double> 
calc_max_in_rows(const vector<vector<double> > &G)
{
	vector<double> G_max(G.size());
	for (int i = 0; i < G.size(); ++i) {
		G_max[i] = G[i][0];
		for (int j = 1; j < G[i].size(); ++j) {
			G_max[i] = max(G_max[i], G[i][j]);
		}
	}

	return G_max;
}

vector<double>
calc_max_in_cols(const vector<vector<double> > &F)
{
	vector<double> F_max(F[0].size());

	for (int i = 0; i < F_max.size(); ++i) {
		F_max[i] = F[0][i];
		for (int j = 1; j < F.size(); ++j) {
			F_max[i] = max(F_max[i], F[j][i]);
		}
	}
	return F_max;
}



int
main(int argc, char *argv[])
{
	int n_proc;
	int rank;
	int n, m;



	MPI_Init(&argc, &argv);
	MPI_Comm_size(MPI_COMM_WORLD, &n_proc);
	MPI_Comm_rank(MPI_COMM_WORLD, &rank);



//reading and sending n and m;
	if (rank == 0) {
		// this is main process
		cin >> n >> m;
		if (n < m) {
			swap(n, m);
		}
	}

	MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
	MPI_Bcast(&m, 1, MPI_INT, 0, MPI_COMM_WORLD);

//Create and fill its part of matrices F and G
	srand(time(NULL));
	vector<vector<double> > F = create_local_matrix(n, m, n_proc, rank);
	vector<vector<double> > G = create_local_matrix(n, m, n_proc, rank);

//every process calculate max in every its rows of matrix G and columns of matrix F

	int loc_n = rank < n % n_proc ? n / n_proc + 1 : n / n_proc;

	//columns of F
	vector<double> loc_F_col_max = calc_max_in_cols(F);

	//and rows of G
	vector<double> loc_G_row_max = calc_max_in_rows(G);


//now we gather this local maximums in on common vector

	vector<double> F_max(m);
	MPI_Allreduce(loc_F_col_max.data(), F_max.data(), m, MPI_DOUBLE, MPI_MAX, MPI_COMM_WORLD);

//find nash equilibriums

	vector<pair<int, int> > loc_ans;

	for (int i = 0; i < loc_n; ++i) {
		for (int j = 0; j < m; ++j) {
			if (F[i][j] == F_max[j] && G[i][j] == loc_G_row_max[i]) {
				loc_ans.push_back(make_pair(i, j));
			}
		}
	}


	MPI_Finalize();

}