Участник:S s serov/DSn-метод решения уравнения переноса

Автор текущей версии статьи: Серов Сергей, 417 гр.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Уравнение переноса нейтронов описывает процессы поглощения, рассеяния и размножения, происходящие в ядерном реакторе. Одним из популярных детерминистических методов его решения, как известно, является DSn-метод . Далее описывается DSn-метод решения стационарного одногруппового уравнения переноса нейтронов в 1D плоско-параллельной геометрии с изотропным рассеянием.

Геометрическая модель решаемой задачи имеет следующий вид: перпендикулярно единственной участвующей в рассмотрении оси [math]x[/math] (будем считать, что она направлена слева направо) расположено несколько бесконечных по осям [math]y[/math] и [math]z[/math] плоско-параллельных слоев некоторого вещества (например, урана, свинца, воды, воздуха и т.д.) заданной толщины, прилегающих друг к другу.

Само уравнение переноса (УП) нейтронов записывается в следующем виде:

[math]\mu \frac{dN(x,\mu)}{dx} + \sigma(x)N(x,\mu) = Q(x,\mu),[/math]

где

[math]Q(x,\mu) = \frac{\sigma_S^0(x)}{2}\int_{-1}^1 N(x,\mu')d\mu' + \frac{1}{2}q(x).[/math]

Используемые обозначения:

• [math]\mu = cos(\theta)[/math] --- косинус угла [math]\theta[/math] между направлением полета нейтрона и положительным направлением оси [math]x[/math];
• [math]N(x,\mu)[/math] --- плотность потока нейтронов, летящих в заданном направлении [math]\mu[/math] в слое с координатой [math]x[/math];
• [math]SN(x) = \int_{-1}^1 N(x,\mu')d\mu'[/math] --- скалярный поток нейтронов в точке [math]x[/math];
• [math]\sigma(x)[/math] --- макроскопическое сечение взаимодействия нейтронов со средой в точке [math]x[/math], т.е. коэффициент обобщенного поглощения нейтронов физическим материалом, расположенным в этой точке среды;
• [math]\sigma_S^0(x)[/math] --- изотропное макроскопическое сечение обобщенного рассеяния нейтронов в точке [math]x[/math] среды, т.е. коэффициент обобщенного рассеяния нейтронов в этой точке среды;
• [math]q(x)[/math] --- независимый изотропный источник нейтронов в точке [math]x[/math].

Одногрупповое УП является интегро-дифференциальным. Левая его часть представляет собой обыкновенный дифференциальный оператор, который отвечает за пролет нейтронов через физическую среду. Правая часть УП содержит интеграл столкновений, который отвечает за рождение вторичных частиц в реакциях упругого и неупругого рассеяния, деления нейтронов, реакций типа [math](n,2n)[/math] и других, а также независимый источник нейтронов. Целью решаемой задачи является нахождение плотности потока нейтронов [math]N(x,\mu)[/math] или скалярного потока [math]SN(x)[/math]. Для решения задачи достаточно вычислить только скалярный поток [math]SN(x)[/math], так как дифференциальная плотность потока нейтронов [math]N(x,\mu)[/math] может быть получена из решения ОДУ с известной правой частью, в которую входит скалярный поток [math]SN(x)[/math]. Таким образом, целью расчета является нахождение стационарного (на бесконечности по времени) распределения плотности потока нейтронов [math]N(x,\mu)[/math] и скалярного потока [math]SN(x)[/math].

Для каждого слоя вещества необходимый набор параметров ([math]\sigma[/math] и [math]\sigma_S^0[/math]), задающих его физические свойства, известен, а также известны краевые условия на левом и правом концах рассматриваемой системы. В рассматриваемой постановке задачи мы считаем, что правее [math]x_{max}[/math] находится вакуум, то есть плотность потока нейтронов равна нулю по всем направлениям полета нейтронов, влетающих справа налево через правую границу системы: [math]N(x_{max},\mu) = 0, \forall \mu \in [-1, 0][/math]. На левой границе [math]x_{min}[/math] заданы точно такие же вакуумные краевые условия для нейтронов, влетающих слева направо через левую границу системы: [math]N(x_{min},\mu) = 0, \forall \mu \in [0, 1][/math]. Также значения параметров [math]\sigma(x), \sigma_S^0(x)[/math] и [math]q(x)[/math] будем считать постоянными в каждом из слоев. Слой с одинаковыми макросечениями и независимым источником нейтронов будем также называть областью.

Для численного решения задачи вводятся 2 одномерные дискретные сетки: по оси [math]x[/math] и по косинусу угла [math]\mu[/math].

Поэтому данный метод решения УП нейтронов и получил название метода дискретных ординат (по [math]\mu[/math] на плоскости [math](x,\mu)[/math]), или DSn – метода.

Альтернативными методами решения этого уравнения являются метод характеристик, метод Монте-Карло и некоторые другие.

1.2 Математическое описание алгоритма

Входные данные:

• геометрическая модель задачи (количество слоев, их расположение на оси [math]x[/math] и толщина);
• [math]\sigma(x)[/math] для каждого слоя;
• [math]\sigma_S^0(x)[/math] для каждого слоя;
• [math]q(x)[/math] для каждого слоя.

Параметры:

• [math]I[/math] --- количество ячеек дискретной сетки по оси [math]x[/math];
• [math]M[/math] --- количество ячеек дискретной сетки по параметру [math]\mu[/math];
• [math]\nu_0[/math] --- количество итераций по правой части УП.

Выходные данные:

• [math]SN(x)[/math] для каждой ячейки введенной сетки.

Введем дискретную сетку по [math]x[/math] и по [math]\mu[/math]:

[math]\mathbb{X} = \{x_i, i \in \{1, \dots, I + 1\} | x_{i+1} = x_i + \Delta x, x_1 = x_{min}, \Delta x = \frac{x_{max} - x_{min}}{I}\},[/math]

[math]\mathbb{M} = \{\mu_m, m \in \{1, \dots, M + 1\} | \mu_{m+1} = \mu_m + \Delta \mu, \mu_1 = -1, \Delta \mu = \frac{2}{M}\}.[/math]

Середины ячеек соответствующих сеток будем обозначать как [math]x_{i+1/2}[/math] и [math]\mu_{m+1/2}[/math].

Алгоритм решения задачи выглядит так:

1. Задается некоторое начальное неотрицательное распределение нейтронов в системе [math]SN_{i+1/2}[/math].
2. Для решения интегро-дифференциального УП нейтронов используем метод итераций источника, то есть организуем итерации [math]\nu[/math] по правой части УП, которая называется источником (он является суммой интеграла столкновений и независимого источника нейтронов). Независимый источник [math]q_{i+1/2}[/math] от номера итерации не зависит и является постоянным на всех итерациях. Интеграл столкновений [math]SN_{i+1/2}[/math] нужно перевычислять на каждой итерации. Более конкретно, по уже известному с предыдущей итерации или из краевого условия распределению [math]SN_{i+1/2}[/math] вычисляем правую часть УП, то есть [math]Q_{i+1/2}[/math] для всех [math]i \in \{1, \dots, I\}[/math]. Далее задача сводится к решению ОДУ на каждой итерации по правой части УП.
3. Алгоритм решения ОДУ на каждой итерации по правой части является неоднородным. Сначала рассчитываются все направления полета нейтронов с отрицательными [math]\mu[/math]. При этом на правой границе системы задаются вакуумные краевые условия, то есть [math]N(x_{max},\mu)=0[/math] для всех [math]\mu \lt 0[/math]. Расчет по [math]x[/math] ведется справа налево, то есть по убыванию индекса [math]i+1/2[/math].
4. Рассчитываем все направления [math]\mu_{m+1/2} \gt 0[/math]. При этом порядок расчета по координате [math]x[/math] будет следующим: от левой границы системы [math]x_{min}[/math] к правой [math]x_{max}[/math], то есть по возрастанию индекса [math]i+1/2[/math]. Чтобы "оттолкнуться" от левой границы [math]x_{min}[/math] используем вакуумные краевые условия [math]N(x_{min},\mu) = 0, \forall \mu \in [0, 1][/math]. Продолжаем для случая [math]\mu \gt 0[/math] накапливать массив [math]SN_{i+1/2}^{new}[/math]. В конце расчета всех [math]\mu_{m+1/2}[/math] в массиве [math]SN_{i+1/2}^{new}[/math] уже насчитаны новые значения [math]SN[/math] для следующей итерации [math]\nu[/math]. Их нужно только присвоить в нужном месте программы снова в массив [math]SN_{i+1/2}[/math].
5. Теперь опишем метод решения обыкновенного дифференциального уравнения с известной правой частью и используемые для этого разностные схемы. Также учитываем, что в указанной постановке задачи параметры [math]\sigma(x), \sigma_S^0(x)[/math] и [math]q(x)[/math] заданы постоянными для каждого слоя. Это необходимо проделать как для положительных, так и для отрицательных значений [math]\mu[/math] при проходах слева направо и справа налево. Далее приводятся формулы для прохода слева направо.

   Уравнение имеет вид:

    :[math]\mu_{m+1/2} \frac{dN(x,\mu_{m+1/2})}{dx} + \sigma(x)N(x,\mu_{m+1/2}) = Q(x,\mu_{m+1/2}).[/math]

   Проинтегрируем его по ячейке [math]T_{i+1/2} = [x_i, x_{i+1}][/math] и получим уравнение баланса нейтронов (сечение взаимодействия нейтронов со средой [math]\sigma(x) = Const[/math] в каждой области вещества и может быть вынесено за знак интеграла):

    :[math]\mu_{m+1/2}(N_{i+1} - N_i) + \sigma(x) \int_{x_i}^{x_{i+1}} N(x,\mu_{m+1/2})dx = \int_{x_i}^{x_{i+1}} Q(x,\mu_{m+1/2})dx.[/math]

   Далее по теореме о среднем:

    :[math]\int_{x_i}^{x_{i+1}} N(x,\mu_{m+1/2})dx = \bar{N}\cdot \Delta x, \int_{x_i}^{x_{i+1}} Q(x,\mu_{m+1/2})dx = \bar{Q}\cdot \Delta x, \Delta x = x_{i+1} - x_i.[/math]

   Тогда уравнение (называемое уравнением баланса) примет вид:

    :[math]\mu_{m+1/2}(N_{i+1} - N_i) + \sigma \bar{N} \Delta x = \bar{Q} \Delta x.[/math]

6. При решении УП нейтронов на основе традиционного DSn-метода обычно используются 2 основные конечно-разностные схемы: DD (diamond difference) – алмазная и St (step) – шаговая. Приведем далее формулы, соответствующие случаю расчета всех направлений полета нейтронов с положительными [math]\mu[/math]. Напомним, что в этом случае расчет по координате [math]x[/math] ведется по возрастанию индекса [math]i+1/2[/math]. Для случая [math]\mu \lt 0[/math] формулы для DD– и St– схем выводятся аналогично.

   St-схема (шаговая) ([math]\bar{N} = N_{i+1})[/math]:

    :[math]\bar{N} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}, N_{i+1} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}.[/math]

   DD-схема (алмазная) ([math]\bar{N} = \frac{1}{2}(N_i + N_{i+1}), N_{i+1} = 2\bar{N} - N_i[/math]):

    :[math]\bar{N} = \frac{\bar{Q} \Delta x + 2\mu_{m+1/2} N_i}{\sigma \Delta x + 2\mu_{m+1/2}}, N_{i+1} = \frac{2\bar{Q} \Delta x + (2\mu_{m+1/2} - \sigma \Delta x) N_i}{\sigma \Delta x + 2\mu_{m+1/2}}.[/math]

   Алмазная DD-схема имеет 2-ой порядок аппроксимации и поэтому является более точной, чем St-схема 1-го порядка аппроксимации, однако не обладает свойствами положительности и монотонности, в отличие от последней, вследствие чего в некоторых случаях может давать отрицательные значения плотности потока, что недопустимо с точки зрения физики явления (невозможно в реальной физической ситуации). В связи с этим традиционный DSn–метод использует обе конечно-разностные схемы для обеспечения, с одной стороны, максимальной точности разностного решения, а с другой – гарантированной его неотрицательности, то есть физичности.

   Переключающий критерий устроен следующим образом: если использование алмазной DD-схемы в какой либо ячейке сетки приводит к отрицательным значениям плотности потока внутри ячейки или на выходе из нее, то расчет этой же ячейки сетки проводится на основе использования шаговой St-схемы, гарантирующей неотрицательность сеточного решения.

В случае использования подробных дискретных сеток время работы приведенного алгоритма может быть достаточно большим. В этом случае актуальной задачей является распараллеливание этого алгоритма.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма состоит из вычисления значений плотности потока нейтронов в каждой ячейке сетки по оси [math]x[/math] для каждого значения косинуса направления полета нейтронов в соответствии с выбранными разностными схемами.

1.4 Макроструктура алгоритма

Как и записано в описании ядра алгоритма, основную часть составляет решение обыкновенного дифференциального уравнения с помощью алмазной и шаговой (при необходимости) разностных схем.

1.5 Схема реализации последовательного алгоритма

1. Задать неотрицательное распределение скалярного потока нейтронов [math]SN[/math] в системе.
2. На каждой итерации:
   1. Вычислить правую часть УП для каждой ячейки двумерной сетки по [math]x[/math] и [math]\mu[/math]: [math]Q(x,\mu) = \frac{\sigma_S^0(x)}{2}\int_{-1}^1 N(x,\mu')d\mu' + \frac{1}{2}q(x)[/math].
   2. Провести вычисление плотностей потока нейтронов в каждой ячейке двумерной сетки справа налево по оси [math]x[/math] с использованием алмазной и шаговой (при необходимости) разностных схем:

      St-схема (шаговая) ([math]\bar{N} = N_{i+1})[/math]:

       :[math]\bar{N} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}, N_{i+1} = \frac{\bar{Q} \Delta x + \mu_{m+1/2} N_i}{\sigma \Delta x + \mu_{m+1/2}}.[/math]

      DD-схема (алмазная) ([math]\bar{N} = \frac{1}{2}(N_i + N_{i+1}), N_{i+1} = 2\bar{N} - N_i[/math]):

       :[math]\bar{N} = \frac{\bar{Q} \Delta x + 2\mu_{m+1/2} N_i}{\sigma \Delta x + 2\mu_{m+1/2}}, N_{i+1} = \frac{2\bar{Q} \Delta x + (2\mu_{m+1/2} - \sigma \Delta x) N_i}{\sigma \Delta x + 2\mu_{m+1/2}}.[/math]

   3. Вычислить скалярный поток нейтронов в каждой ячейке сетки по [math]x[/math] путем интегрирования плотностей потока нейтронов по всем значениям косинуса угла полета [math]\mu[/math]: [math]SN(x) = \int_{-1}^1 N(x,\mu')d\mu'[/math].

1.6 Последовательная сложность алгоритма

Умножения и сложения (вычитания) составляют основную часть алгоритма.

Для решения уравнения переноса DSn-методом на каждой итерации требуется:

[math]O(I*M)[/math] умножений и сложений.

Таким образом, последовательная сложность всего алгоритма составляет:

[math]O(\nu_0*I*M)[/math] умножений и сложений.

При классификации по последовательной сложности, таким образом, DSn-метод решения УП относится к алгоритмам с линейной сложностью.

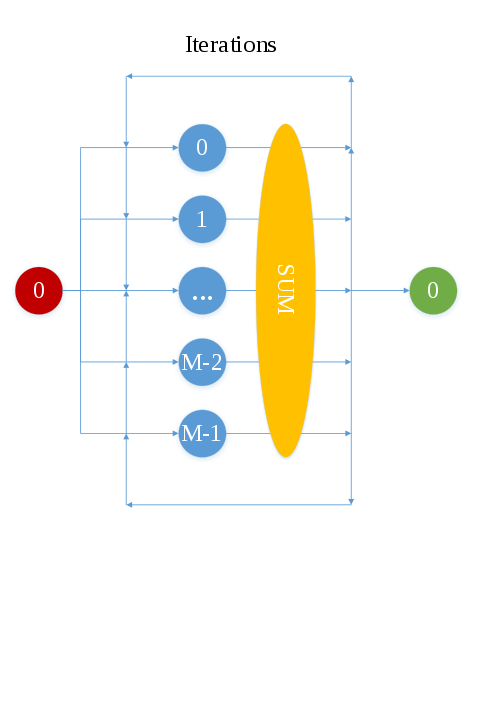
1.7 Информационный граф

Красным цветом обозначена вершина процесса, считывающего данные, формирующего массивы исходных данных и рассылающего их всем остальным запущенным процессам, число которых меньше либо равно числу ячеек введенной сетки по [math]\mu[/math].

Синим цветом обозначены вершины всех процессов, которые для определенных ячеек сетки по [math]\mu[/math] на каждой итерации вычисляют сначала правую часть УП, а затем с помощью разностных схем --- значения плотности потока нейтронов во всех ячейках оси [math]x[/math].

Желтым цветом обозначена вершина, отвечающая операции суммирования значений, насчитанных каждым процессом, и их рассылки всем участвующим в вычислениях процессам.

Зеленым цветом обозначена вершина процесса, который, после завершения процессами выполнения всех итераций, собирает окончательные значения скалярного потока нейтронов в одном массиве и выводит результат работы.

1.8 Ресурс параллелизма алгоритма

Имея в распоряжении [math]M[/math] процессов, мы имеем возможность производить вычисления плотности потоков нейтронов в ячейках сетки по оси [math]x[/math] для разных значений косинуса угла полета [math]\mu[/math] независимо друг от друга. Это означает, что каждый процесс по отдельности может вычислять правую часть уравнения переноса, а затем и решать его с использованием разностных схем для некоторых выделенных ему значений параметра [math]\mu[/math], а лишь затем, в конце итерации, обмениваться вычисленными значениями с другими процессами для пересчета правой части уравнения.

Таким образом, сложность параллельной реализации будет составлять

[math]O(\nu_0*I)[/math] умножений и сложений.

1.9 Входные и выходные данные алгоритма

Входные данные: массив [math]\sigma(x)[/math] для каждого слоя, массив [math]\sigma_S^0(x)[/math] для каждого слоя, массив [math]q(x)[/math] для каждого слоя.

Объем входных данных: [math]3k[/math], где [math]k[/math] --- количество слоев в геометрии задачи.

Выходные данные: массив [math]SN(x)[/math] для каждой ячейки введенной сетки.

Объем выходных данных: [math]N[/math], где [math]N[/math] --- количество ячеек введенной сетки по [math]x[/math].

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

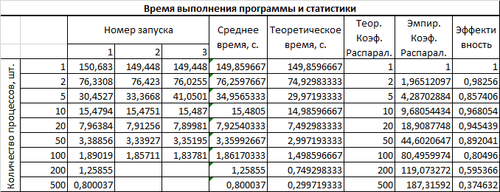
Приведем результаты запусков параллельной реализации DSn-метода решения УП для на суперкомпьютере "Ломоносов" для разного числа процессов. Использованные параметры: число ячеек сетки по оси [math]x[/math]: [math]I = 80000[/math], число ячеек сетки по оси [math]\mu[/math]: [math]M = 1000[/math], количество итераций метода [math]\nu_0 = 50[/math].

В прикрепленной таблице содержатся времена выполнения программы в секундах для разного числа запущенных процессов. В следующих столбцах указаны среднее время по 3-м запускам (для 200 и 500 процессов --- по 1-му), теоретическое время работы программы (рассчитанное как отношение времени работы на одном процессе к количеству параллельных процессов), теоретический и эмпирический коэффициенты распараллеливания (рассчитанные как отношение теоретического и эмпирического времени работы на нескольких процессах ко времени работы на одном процессе) и коэффициент эффективности (рассчитанный как отношение эмпирического коэффициента распараллеливания к теоретическому).

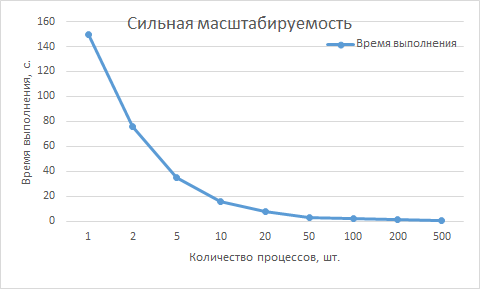
Построим график зависимости времени выполнения программы от количества параллельных процессов, иллюстрирующий сильную масштабируемость алгоритма.

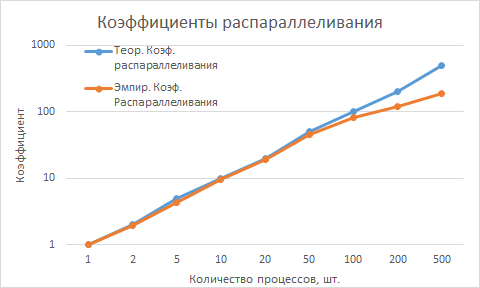
Построим графики теоретического и эмпирического коэффициентов распараллеливания в зависимости от количества использованных параллельных процессов.

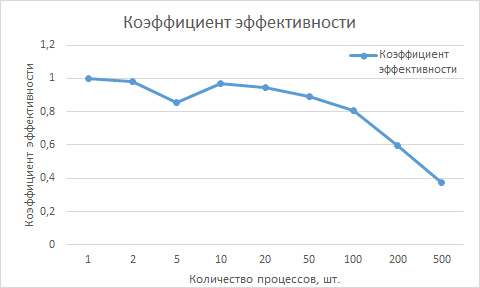
Построим график коэффициента эффективности в зависимости от количества использованных параллельных процессов.

DSn-метод обладает свойством сильной масштабируемости, потому что график сильной масштабируемости имеет сильно выпуклый вид наподобие функции [math]\frac{1}{n}[/math]. Из графика коэффициентов распараллеливания видно, что при увеличении числа параллельных процессов до 200 и выше издержки на пересылку данных между процессами становятся значительнее, и график эмпирического коэффициента отклоняется от графика теоретического. Визуально это отклонение отражено на последнем графике, который свидетельствует о том, что при использовании до 100 процессов эффективность распараллеливания составляет более 0.8, что является очень хорошим показателем, а нижнего приемлемого значения 0.35 она почти достигает при числе процессов, равном 500. Это означает, что использование большего числа процессов в одном параллельном запуске будет уже неэффективно.

Заметим. что при количестве процессов, равном 5, наблюдается заметное уменьшение эффективности. Это связано с тем, что запускается нечетное число процессов и взаимодействие между ними происходит медленнее, чем для четного числа процессов.

2.4.2 Характеристики программно-аппаратной среды

Все вычисления были произведены на суперкомпьютере "Ломоносов".

Для компиляции был использован компилятор языка C++ GNU 4.4.6, реализация MPI: Intel MPI 4.0.3.

Вычисления производились в сегментах test, regular4 и regular6. Ограничений на время выполнения программы наложено не было.

3 Литература

<references \>