Участник:Grinch96/QR-факторизация методом Грама-Шмидта с последующей реортогонализацией

Автор: Г. А. Балыбердин

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Пусть [math]A = (a_1, ..., a_n)[/math] - вещественная матрица [math]n × n[/math], определитель которой не равен [math]0[/math]. Во многих приложениях требуется решать линейную систему [math]Ax=b[/math] c плохо-обусловленной матрицей [math]A[/math]. При решении данной задачи, чтобы не увеличивать число обусловленности матрицы [math]A[/math], ее можно представить в виде [math]A=QR[/math], где матрица [math]Q \in \mathbb{R}^{n×n}[/math] состоит из ортонормированных строк, а матрица [math] R \in \mathbb{R}^{n×n}[/math] является верхнетреугольной. В итоге мы получаем так называемую [math]QR[/math]-факторизацию.

Чтобы построить [math]QR[/math]-факторизацию можно воспользоваться процессом ортогонализации Грама-Шмидта, однако в условиях машинной арифметики, матрица [math]Q[/math] может получиться далекой от ортогональной.Чтобы этого избежать, на определенных итерациях нужно проводить процесс реортогонализации .

1.2 Математическое описание алгоритма

Исходные данные: квадратная матрица [math]A[/math] порядка [math]n[/math] (элементы [math]a_{ij}[/math]), определитель которой не равен [math]0[/math].

Вычисляемые данные: верхнетреугольная матрица [math]R[/math] порядка [math]n[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] порядка [math]n[/math] (элементы [math]q_{ij}[/math]); выполняется соотношение [math]QR=A[/math].

Формулы процесса ортогонализации:

[math] \begin{align} & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ & q_{j} = p_{j} / ||p_{j}||_{2}, \\ & r_{ij} = q_{i}^{T} a_{j},\quad i = 1, \ldots , j - 1.\\ \end{align} [/math]

Здесь [math]q_{i}, \, a_{i} [/math] столбцы матриц [math] Q, \, A [/math] соответственно.

На [math]m[/math]-ом шаге получаем [math]p_{m} \in \mathbb{R}^{n}[/math]. Если [math]||a_{m}||_{2}/||p_{m}||_{2} \gt k[/math], запускается процесс реортогонализации. [math]k[/math] произвольная и задает точность ортогональности матрицы [math]Q[/math]. В посвященной методу реортогонализации статье [math]k[/math] рекомендуется брать равным [math]10[/math], однако приводятся примеры алгоритмов, где [math]k=\sqrt{2}[/math] или [math]k=\sqrt{5}[/math]. Мы исследуем [math]k=10[/math].

Суть процесса реортогонализации - это процесс ортогонализации Грама-Шмидта, примененный повторно к вектору [math]p_{m}[/math] на [math]m[/math]-оm шаге алгоритма. Более формально:

[math] \begin{align} & \tilde{p}_{m} = p_{m} - \sum_{i=1}^{m-1} q_{i} (q_{i}^{T} p_{m}), \\ & q_{m} = \tilde{p}_{m} / ||\tilde{p}_{m}||_{2}, \\ & \tilde{r}_{mj} = q_{j}^{T} p_{m}, \quad j = 1, \ldots , m - 1, \\ & r_{mj} = \tilde{r}_{mj} + r_{mj}^{0}, \quad j = 1, \ldots , m - 1, \\ & r_{mm} = ||\tilde{p}_{m}||_{2}. \end{align} [/math]

Здесь [math]\tilde{q}_{i}[/math] столбцы матриц [math] \tilde{Q}_{m}[/math], [math]r_{mj}^{0}[/math] - элементы матрицы [math]R[/math], вычисленные до реортогонализации.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма, если не требуется реортогонализация, состоит из вычисления:

• [math]\dfrac{n(n+1)}{2}[/math] скалярных произведений векторов, включая вычисление длины вектора;

• [math]\dfrac{(n-1)n}{2}[/math] умножений векторов на число.

На каждом шаге реортогонализации добавляется [math] j-1 [/math] вычислений скалярных произведений векторов на число и столько же умножений вектора на число. Здесь реортогонализация производится на [math]j[/math]-ом шаге. Однако сколько раз алгоритм будет реортогонализовывать вектора зависит от свойств матрицы.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть процесса составляют скалярные произведения векторов и умножения вектора на число:

[math] \begin{align} & p_{j} = a_{j} - \sum_{i=1}^{j-1} q_{i} (q_{i}^{T} a_{j}), \\ & q_{j} = p_{j} / ||p_{j}||_{2}. \end{align} [/math]

как если алгоритм реортогонализует повторно вектора, так и без реортогонализаций.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения процесса следующая:

1. [math] q_1 = \frac{a_1}{||a_1||_2} [/math]

Далее для всех [math] i = 2, n [/math]:

2. [math] r_{ij} = q_{j}^{T} a_{i},\quad j = 1, \ldots , i - 1 [/math]

3. [math] p_{i} = a_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}[/math]

Если [math]||a_{i}||_{2}/||p_{i}||_{2} \gt k[/math], выполнить 4, 5, 6. Иначе перейти сразу к 7:

4. [math] r_{ij}^{0} = q_{j}^{T} p_{i},\quad j = 1, \ldots , i - 1 [/math]

5. [math] p_{i} = p_{i} - \sum_{j=1}^{i-1} q_{j} r_{ij}^{0}, \quad j = 1, \ldots , i - 1 [/math]

6. [math] r_{ij} = r_{ij}^{0} + r_{ij},\quad j = 1, \ldots , i - 1 [/math]

7. [math] r_{ii} = ||p_{i}||_{2} [/math]

8. [math] q_{i} = p_{i} / r_{ii} [/math]

Здесь (как и везде) под второй нормой подразумевается:

[math] ||x||_2 = \sqrt{x_1^2 + x_2^{2} + \ldots + x_n^2} [/math]

1.6 Последовательная сложность алгоритма

Для факторизации матрицы порядка n процессом Грама-Шмидта в последовательном варианте без реортогонализации требуется:

• [math]n[/math] извлечений квадратного корня,
• [math]n[/math] делений,
• [math](n-1)(n^2+2n-1)[/math] сложений (вычитаний),
• [math]n(n^2+2n-2)[/math] умножений.

Если реортогонализация работает на каждом шаге (чего никогда не случается, однако предположим худший случай), то количество всех операций удвоится. Таким образом, умножения и сложения (вычитания) составляют основную часть алгоритма.

При классификации по последовательной сложности, процесс ортогонализации Грама-Шмидта с реортогонализацией относится к алгоритмам с кубической сложностью.

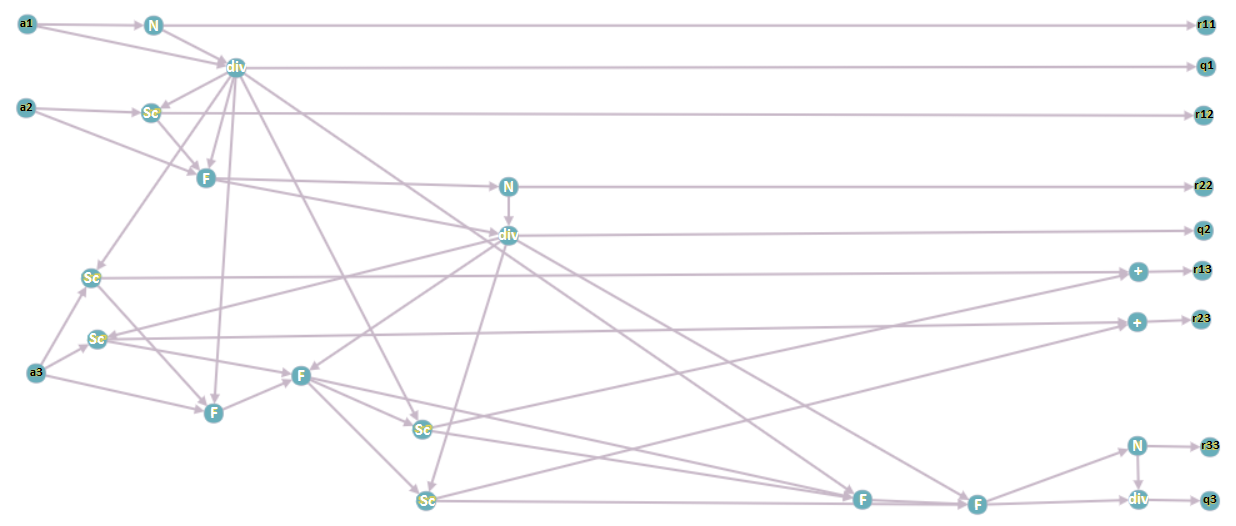
1.7 Информационный граф

Опишем вершины информационного графа.

1. [math] a_i, \; i = 1 \ldots n [/math] — столбцы исходной матрицы [math] A [/math]; подаются на вход программе.

2. [math] N [/math] — операция взятия нормы вектора.

3. [math] div [/math] — операция деления вектора на число.

4. [math] Sc [/math] — операция взятия скалярного произведения двух векторов.

5. [math] F [/math] — операция вычитания из вектора произведение числа на вектор.

6. [math] + [/math] — операция суммирования двух чисел.

7. [math] r_{ij} [/math], [math] q_i, \; i = 1 \ldots n, \; j = 1 \ldots n [/math] — элементы матрицы [math] R [/math] и столбцы матрицы [math] Q [/math] соответственно; выходные данные программы.

Информационный граф построен для матрицы размерности [math] 3 [/math] при выполнении реортогонализации для третьего вектора.

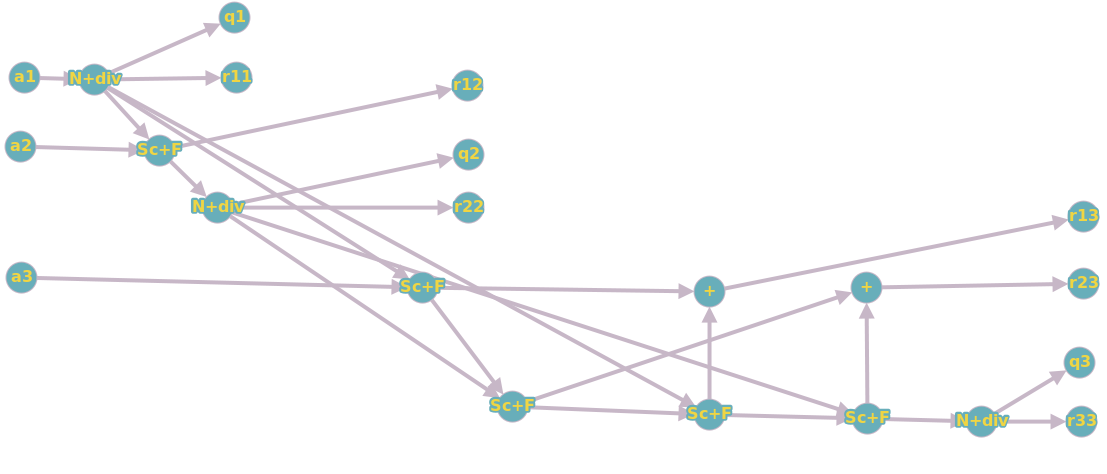
Если объединить вершины N и div, Sc и F (вершины будут означать суперпозиции соответствующих операций), то получится следующий, чуть более простой для понимания, граф:

1.8 Ресурс параллелизма алгоритма

В последовательной версии алгоритма двумя самыми трудоемкими операциями являются подсчет скалярных произведений и вычисление вектора, ортогонального предыдущим. Мы хотим добиться, чтобы каждый процессор считал "кусок" этих операций, однако также для ускорения работы программы нужно минимизировать число пересылок между процессорами. Пусть [math] k [/math] - количество процессоров. Предлагается разбить исходную матрицу [math] A [/math] на [math] k [/math] блоков по [math] \frac{n}{k} [/math] столбцов в каждом ([math] n [/math] - размерность задачи), тогда каждый процессор будет решать задачу на "своем подпространстве". Таким образом мы добьемся количества пересылок порядка [math] O(kn) [/math], и параллельная сложность алгоритма составит [math] O( \frac{n^3}{k} ) [/math].

1.9 Входные и выходные данные алгоритма

Входные данные: невырожденная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).

Объём входных данных: [math]n^2[/math].

Выходные данные: верхняя треугольная матрица [math]R[/math] (элементы [math]r_{ij}[/math]), унитарная матрица [math]Q[/math] (элементы [math]q_{ij}[/math]).

Объём выходных данных: [math]\frac{n (n + 1)}{2} + n^2[/math] (в силу треугольности матрицы [math]R[/math] достаточно хранить только ее ненулевые элементы).

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

число процессоров [math]2^k[/math], где k пробегает от 0 до 7;

размер матрицы [math]n^p[/math], где p пробегает от 8 до 12.

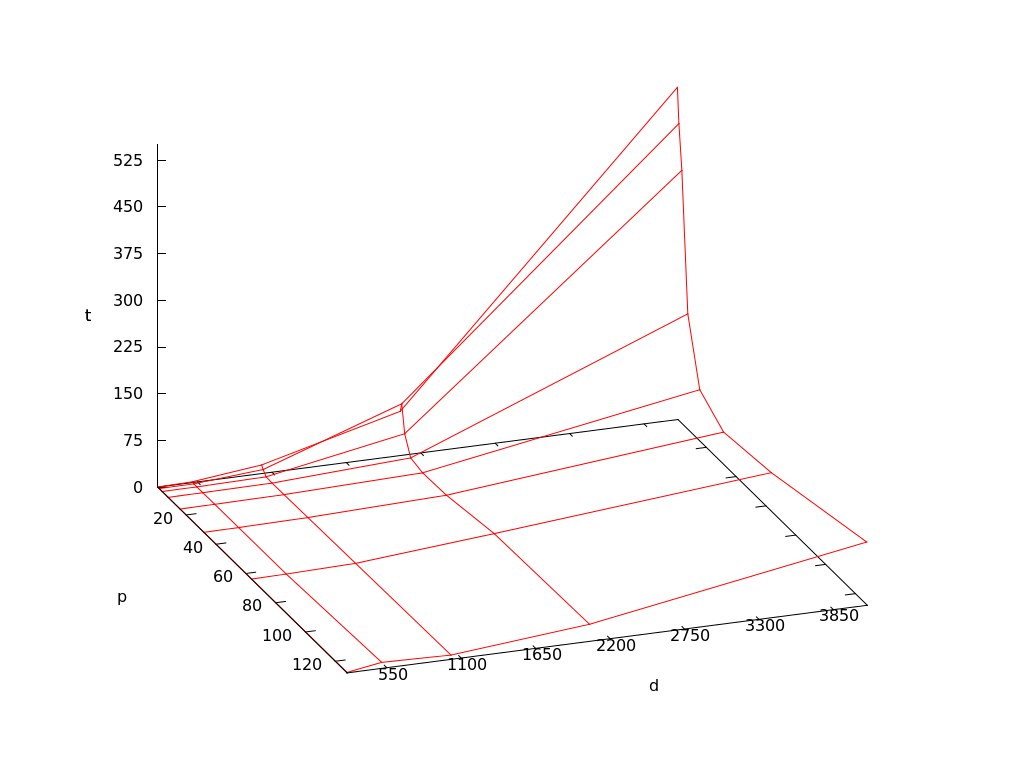
На следующем рисунке приведен график времени работы алгоритма (t) в зависимости от количества процессов (p) и размерности задачи (d):

Сильная масштабируемость на графике наблюдается в тех случаях, когда время пересылок много меньше времени работы процесса. Когда время, затраченное на пересылки, эквивалентно времени работы процесса, на графике мы можем наблюдать слабую масштабируемость. Если же время пересылок начинает превышать время работы процессоров, смысл от параллельности теряется, так как при увеличении числа процессов увеличивается время подсчета.

2.7 Существующие реализации алгоритма

Существует масса реализаций метода Грама-Шмидта без реортогонализации, о которых говорится, например, здесь. Про реализации с реортогонализацией информации нет.

3 Литература

<references \>

[[Категория:]]

[[Категория:]]