Участник:Кинжикеева Дина/ Алгоритм решения линейной системы сравнений

Алгоритм: Алгоритм решения линейной системы сравнений.

Исполнитель: Кинжикеева Дина.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

---

Введем некоторые определения.

Определение 1 Пусть m целое число большее единицы (m>1). Говорят, что a сравнимо с b по модулю m, если m делит (a-b) (обозначение: m|(a-b)), а именно выполняется равенство: a = b+tm, где t некоторое целое число. Сравнение записывает таким образом: [math] a ≡ b   (mod   m) [/math].

Определение 2 Число НОД(a,b) называется наибольшим общим делителем двух чисел a,b если:

1. НОД(a,b) делит оба числа a и b;
2. НОД(a,b) является наибольшим общим делителем чисел a и b, то если d|a и d|b, то d|НОД(a,b) (или, что то же самое, d меньше либо равно НОД(a,b)).

Определение 3 Числа a и b называются взаимно простыми, если НОД(a,b)=1.

Задана линейная система сравнений вида:

[math]x ≡ a_1  (mod   m_1) [/math]

[math]x ≡ a_2  (mod   m_2) [/math]

[math] ... [/math]

[math]x ≡ a_n  (mod   m_n)  , [/math]

где [math]  m_1,m_2,...,m_n [/math] - натуральные взаимно простые числа, [math]   a_1, a_2,..., a_n[/math] -некоторые целые числа.

Рассматривается задача решения линейной системы сравнений вида, описанного выше. Данная система сравнений имеет единственное решение по модулю [math]M=m_1m_2...m_n [/math] по китайской теореме об остатках. Эта теорема утверждает, что можно восстановить целое число по множеству его остатков от деления числа из некоторого набора попарно взаимно простых чисел. Теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы, предположительно датируемом третьим веком н. э. и затем была обобщена Цинь Цзюшао в его книге «Математические рассуждения в 9 главах» датируемой 1247 годом, где было приведено точное решение. Утверждение этой теоремы можно рассматривать как алгоритм решения линейной системы сравнений требуемого вида. Искомое решение ищется как сумма вида:

[math] x= ∑_{i=1}^{n} a_i M_i N_i   (mod   M)  , [/math]

где [math]M_i=M   /   m_i   , [/math] [math]N_i= M_{i}^{-1}  (mod   m_i) [/math].

1.2 Математическое описание алгоритма

Алгоритм строится на утверждении китайской теоремы об остатках.

Теорема. (Китайская теорема об остатках)

Пусть [math]m_1,m_2,...,m_n[/math] натуральные числа такие, что НОД([math]m_i,m_j[/math])=1, при [math]i≠j[/math] для любых [math]i,j=1,2,..,n[/math]. И пусть [math]a_1,a_2,...,a_n[/math] целые числа. Тогда система сравнений вида:

[math]x ≡ a_1  (mod   m_1) [/math]

[math]x ≡ a_2  (mod   m_2) [/math]

[math] ... [/math]

[math]x ≡ a_n  (mod   m_n)  , [/math]

имеет единственное решение по модулю числа [math]M=m_1m_2...m_n[/math]:

[math] x= ∑_{i=1}^{n} a_i M_i N_i   (mod   M)  (1), [/math]

где [math]M_i=M   /   m_i   , [/math] [math]N_i= M_{i}^{-1}  (mod   m_i) [/math].

Доказательство. Докажем существование решения, а именно, что решение [math]x[/math] удовлетворяет заданной системе сравнений. Рассмотрим [math]x   (mod   m_1)[/math]. Все слагаемые в сумме (1), кроме первого, делятся на [math]m_1[/math], а первое слагаемое [math]a_1M_1N_1 ≡ a_1   (mod   m_1)[/math], так как [math]M_1N_1≡1   (mod   m_1)[/math]. Таким образом, [math]x ≡ a_1  (mod   m_1) [/math]. Аналогичным образом для [math]m_2,..,m_n[/math]. Следовательно, [math]x[/math] -решение. Покажем единственность решения. Пусть существуют два различных решения системы [math]x_1[/math] и [math]x_2[/math].

[math]x_0=x_1-x_2[/math]

Тогда для любого [math]i=1,..,n[/math] [math]  m_i|x_0[/math], а следовательно и [math]M|x_0[/math] ([math]M|(x_1-x_2)[/math]). Это означает, что [math]x_1[/math] можно представить в виде: [math]x_1=x_2+kM[/math], [math]k[/math] некоторое целое число. Следовательно, [math]x_1=x_2   (mod   M)[/math], что и требовалось доказать. Теорема доказана.

Поэтапное описание алгоритма:

1. Вычисление значения [math]M[/math].

   [math]M=m_1m_2...m_n[/math]

2. Вычисление значений [math]M_i[/math], для всех [math]i=1,...,n[/math].

   [math]M_i=M/m_i[/math]

3. Нахождение обратных элементов к [math]M_i[/math] по соответствующему модулю при помощи алгоритма Евклида. Описание расширенного алгоритма Евклида:

   [math]a^{-1}  (mod   b) [/math]

   [math]t_0=a   t_1=b [/math]

   [math]t_0=t_1q_1+t_2[/math]

   [math]t_1=t_2q_2+t_3[/math]

   [math]...[/math]

   [math]t_{k-2}=t_{k-1}q_{k-1}+t_{k}   t_{k}=1 [/math]

   [math]t_{k-1}=t_{k}q_{k}[/math]

   [math]p_0=1   p_1=q_1[/math]

   [math]p_j=q_jp_{j-1}+p_{j-2}   j=2,...,k [/math]

   [math]a^{-1}=(-1)^{k+1}p_{k-1}[/math]

4. Формирование итогового ответа.

   [math] x=a_1 M_1 N_1+...+a_n M_n N_n   (mod   M)[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляет определение для каждого числа [math]M_i=M/m_i[/math] , [math]i=1,..., n[/math], обратного к нему числа по модулю [math]m_i[/math] при помощи расширенного алгоритма Евклида.

1.4 Макроструктура алгоритма

В алгоритм последовательно входят следующие макроструктуры:

1. Вычисление [math]M_i[/math] как произведение всех [math]m_j[/math] для всех [math]j≠i, j =1, ...,n [/math];
2. Вычисление обратного числа к [math]M_i[/math] по расширенному алгоритму Евклида;
3. Суммирование произведений вида [math]a_i M_i N_i[/math], [math]i=1, ...,n [/math], по модулю [math]M[/math].

1.5 Схема реализации последовательного алгоритма

Общая схема реализации программы:

[math]for   i:=0   to   n [/math]

[math]M=M*m_i;[/math]

[math]for   i:=0   to   n [/math]

[math]M_i=M/m_i;[/math]

[math]M_{i}^{-1}=РасширенныйАлгоритмЕвклида(M_i,m_i);[/math]

[math]x=x+a_i*M_i*M_{i}^{-1};[/math]

[math]x=x  mod   M;[/math]

Предлагаемая реализация Расширенного Алгоритма Евклида (С/С++):

int inverse(int a, int m) {//a<m

int c,cur=0, q,p0=0,p1=1,p2,m0=m;

while (a) {

cur++;

c = m % a;

q = (m-c)/a;

p2 = q*p1+p0;

p0 = p1;

p1 = p2;

m = a;

a = c;

}

if (m==1) {

if (cur%2)

return p0;

return m0-p0;

}

return -1;

}

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма составляет [math]3nlogk[/math], где [math]k[/math] равен максимальному значению [math]M_i[/math], [math]i=1, ...,n [/math]. Основная сложность приходится на расчет обратного элемента к [math]M_i[/math] по модулю [math]m_i[/math] по расширенному Алгоритму Евклида, т.к при работе алгоритма Евклида (не расширенного) совершается максимальное число шагов [math]log(max\{a,b\})[/math], когда подаются на вход числа [math]a[/math] и [math]b[/math] взаимно простые (по условию данной задачи рассматриваются только такие числа), и число шагов в расширенном алгоритме совпадает, то исходя из предложенной реализации расширенного Алгоритма Евклида сложность его работы составит [math]3logk[/math]. Всего данный алгоритм будет отрабатывать [math]n[/math] раз, следовательно сложность Алгоритм решения линейной системы сравнений составит [math]3nlogk[/math].

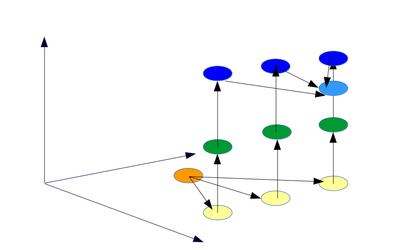
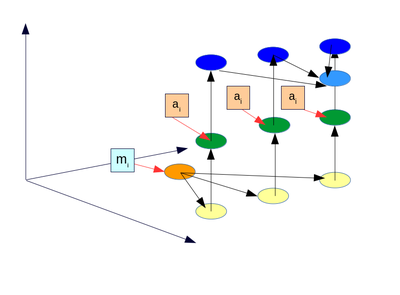
1.7 Информационный граф

Описание графа алгоримта. В графе алгоритма в яросно-параллельной форме выделяется 3 яруса (см. рис.1). Первый ярус: расчет [math]M[/math] и [math]M_i[/math]. Второй ярус: умножение вида [math]M_ia_i[/math]. Третий ярус: растчет [math]M_{i}^{-1}[/math] по расширенному Алгоритму Евклида, и формирование итогового ответа как сумму [math]M_ia_iM_{i}^{-1}[/math]. Во всех ярусах [math]i=1, ..., n[/math].

рис.1 Информационный граф. Оранжевый- операция 1 (п. 1.2); желтый -операции 2 (п. 1.2); зеленый- операция умножения на ai ;синий-операции 3 (п. 1.2), голубой -операция 4 (п. 1.2).

Входные данные [math]m_i[/math] подаются на первый ярус, [math]a_i[/math] -на второй (см. рис.2).

рис.2 Информационный граф с изображением входных данных.] Оранжевый- операция 1 (п. 1.2); желтый -операции 2 (п. 1.2); зеленый- операция умножения на ai ;синий-операции 3 (п. 1.2), голубой -операция 4 (п. 1.2).

1.8 Ресурс параллелизма алгоритма

Для реализации алгоритма решения линейной системы сравнений потребуется выполнить последовательно следующие ярусы:

• 1 раз первый ярус
• 1 раз второй ярус
• [math]3*log(k)+1[/math] раз третий ярус, где [math]k[/math] равен максимальному значению [math]M_i[/math], [math]i=1, ...,n [/math].

Таким образом параллельная сложность алгоритма составит [math]3logk+2[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: [math]n[/math] пар числе [math](a_i, m_i)[/math], соответствующая линейному сравнению вида [math] x ≡ a_i  (mod   m_i) [/math] , где [math]m_i[/math] - натуральные взаимно простые числа, [math] a_i[/math] -некоторые целые числа, [math]i=1, ..., n[/math].

Объем входных данных: [math]2n[/math].

Выходные данные: число [math]x[/math] - решение линейной системы сравнений.

Объем выходных данных: [math]1[/math].

3 Литература

1. Применко Э.А. Алгебраические основы криптографии: Учебное пособие. M.:Книжный Дом "ЛИБРОКОМ",2013.-288с.
2. Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И. Защита информации: учебное пособие — М.: МФТИ, 2011. — 225 с. — ISBN 978-5-7417-0377-9
3. Переславцева О. Н. Распараллеливание алгоритмов с применением китайской теоремы об остатках. — Вестник ТГУ, 2009. — № 4. — ISSN 1810-0198.