Участник:Valkyrie/Адаптивное интегрирование

Адаптивное интегрирование

Автор: В.А. Мастинен

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Адаптивное интегрирование - это метод численного интегрирования, в котором интеграл функции [math]f(x)[/math] аппроксимируется с использованием статических квадратурных формул на адаптивно уточненных подынтервалах области интегрирования. Как правило, адаптивные алгоритмы столь же эффективны, как и традиционные алгоритмы для «достаточно гладких» подынтегральных функций, но также неэффективны для «плохих» подынтегральных функций, на которых традиционные алгоритмы терпят неудачу.

Из анализа погрешностей методов численного интегрирования следует, что точность получаемых результатов зависит как от характера изменения подынтегральной функции, так и от шага интегрирования. При этом ясно, что для достижения сравнимой точности при интегрировании слабо меняющейся функции шаг можно выбирать большим, чем при интегрировании резко меняющихся функций.

На практике нередко встречаются случаи, когда подынтегральная функция меняется по-разному на отдельных участках отрезка интегрирования. Это обстоятельство требует такой организации численного алгоритма, при котором он автоматически приспосабливался к характеру изменения функции -вводил разные значения шага интегрирования на отдельных участках отрезка интегрирования. Это позволяет уменьшить машинное время без потери точности результатов расчета. Такой подход используется обычно при задании подынтегральной функции [math]f(x)[/math] в виде формулы, а не в табличном виде.

1.2 Математическое описание алгоритма

Исходные данные : интегрируемая функция [math]f(x)[/math], определенная на отрезке [math][a,b][/math], допустимая погрешность интегрирования [math]\varepsilon[/math].

Вычисляемые данные : приближенное значение [math]Q[/math] интеграла [math]\int\limits_a^b f(x)\,dx[/math].

Пусть [math]Q(a,b)[/math] - квадратурная формула, аппроксимирующая значение интеграла на отрезке [math][a,b][/math].

Оценим [math]\tau \approx |Q(a,b) - \int\limits_a^b f(x)\,dx|[/math].

Если [math]\tau \gt \varepsilon[/math], поделим отрезок [math][a,b][/math] пополам и применим этот же алгоритм к каждому из отрезков [math][a,c][/math] и [math][c,b][/math], где [math] c = \frac{a+b}2 [/math], задав погрешность интегрирования на каждом из отрезков [math]\frac{\varepsilon}2[/math].

Если в качестве квадратурной формулы выбрать формулу Симпсона, то [math]\tau[/math] можно положить равным [math]\frac{|Q(a,c) + Q(c,b) - Q(a,b)|}{15}[/math] ().

Далее в качестве квадратурной формулы будет использоваться формула Симпсона.

1.3 Вычислительное ядро алгоритма

Основную часть алгоритма составляют вычисления квадратурной формулы, следовательно, и значений интегрируемой функций в трех точках, на каждом отрезке интегрирования. Так же на каждом отрезке подсчитывается ошибка интегрирования, которая представляет собой разность обычной квадратурной формулы [math]Q(a,b)[/math] и уточненной [math]\tilde{Q}(a,b) = Q(a,c) + Q(c,b)[/math].

1.4 Макроструктура алгоритма

Как уже записано в описании ядра алгоритма, основную часть алгоритма составляют вычисление квадратурной формулы и подсчет ошибки интегрирования на текущем отрезке интегрирования. После чего решается уточнять ли значение квадратурной формулы на данном отрезке или нет.

1.5 Описание схемы реализации последовательного алгоритма

Последовательный алгоритм представляет собой рекурсивный подсчет приближенного значения интеграла на отрезке с заданной допустимой погрешностью. Начальным отрезком является весь отрезок интегрирования. Далее, на каждом шаге рекурсии происходит подсчет трех квадратурных формул - [math]Q(a,b)[/math], [math]Q(a,c)[/math] и [math]Q(c,b)[/math], после чего оценивается погрешность интегрирования [math]\tau = \frac{|Q(a,c) + Q(c,b) - Q(a,b)|}{15}[/math]. Если [math]\tau \lt \varepsilon[/math], тогда приближенным значением интеграла на данном отрезке считаем величину [math]Q(a,c) + Q(c,b)[/math]. Иначе рекурсивно считаем таким же образом приближенные значения интеграла на отрезках [math][a,c][/math] и [math][c,b][/math], задав допустимой погрешностью на каждом отрезке величину [math]\frac{\varepsilon}{2}[/math], а их сумму примем за результат.

1.6 Последовательная сложность алгоритма

Число операций, необходимых для вычисления приближенного значения интеграла, вообще говоря, зависит от допустимой погрешности интегрирования [math]\varepsilon[/math] и от степени гладкости интегрируемой функции [math]f(x)[/math]. Пусть алгоритм разбил [math]k[/math] отрезков пополам, тогда в окончательном разбиении отрезка интегрирования получилось [math]k+1[/math] отрезков. На каждом таком отрезке и на этапе разбиения приходится считать [math]Q(a,b)[/math], [math]Q(a,c)[/math] и [math]Q(c,b)[/math], то есть необходимо произвести вычисление значений [math]f(x)[/math] в 5 точках, для подсчета каждой квадратуры необходимо выполнить 3 сложения, 1 вычитание, 1 умножение и 2 деления, а также 1 сложение, 1 вычитание и 1 деление для проверки критерия разбиения отрезка пополам и 1 деление при каждом разбиении отрезка. Таким образом, получается:

• [math]5(2k+1)[/math] вычислений значения [math]f(x)[/math] в некоторых точках
• [math]6(2k+1) [/math] сложений и вычитаний
• [math]9k+4[/math] делений и умножений

1.7 Информационный граф

На рисунке 1 приведена работа алгоритма при [math]\varepsilon = 4*10^{-6}[/math], [math]a = 0[/math], [math]b = 1[/math] и [math]f(x) = \left\{ \begin{matrix} sin(\pi x) \text{ при } x \in [0, \frac{1}{2}] \text{,} \\ 1 - 4 (x - \frac{1}{2})^2 \text{ при } x \in [\frac{1}{2}, 1] \text{.}\end{matrix} \right. [/math]

Рисунок 1. Квадратики - задачи интегрирования [math]f(x)[/math] на отрезке [math][a,b][/math] при допустимой погрешности [math]\varepsilon[/math], разбиение задачи на 2 происходит при условии [math]\tau \gt \varepsilon[/math]. Оранжевым выделены операции вычисления квадратурной формулы на данном отрезке интегрирования [math]Q(a,b)[/math], желтым - уточненной квадратурной формулы [math]\tilde{Q}(a,b)[/math]. Зеленым отмечены операции оценки ошибки интегрирования [math]\tau[/math]. Фиолетовым выделены операции сложения двух чисел. Красным отмечен результат работы алгоритма.

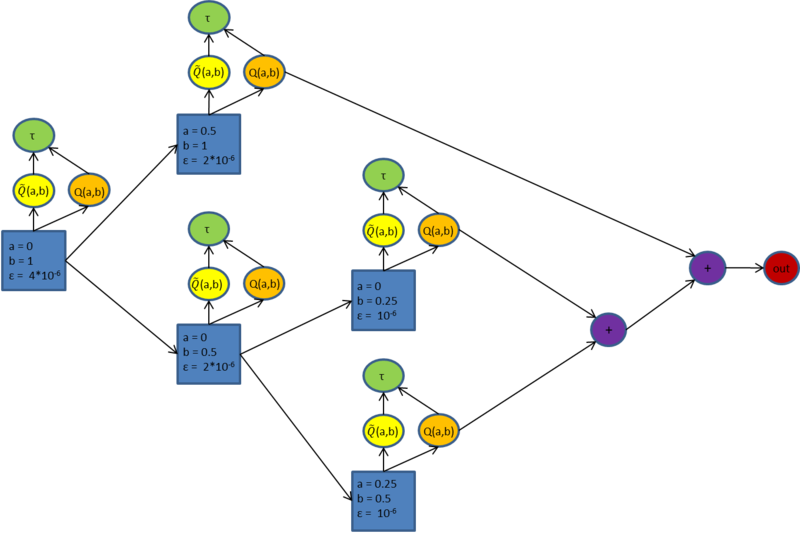
Напомним, что уточненная квадратурная формула вычисляется следующим образом - [math]\tilde{Q}(a,b) = Q(a,\frac{a+b}{2}) + Q(\frac{a+b}{2},b)[/math]

1.8 Ресурс параллелизма алгоритма

Очевидным ресурсом параллелизма данного алгоритма является независимость интегрирования по разным отрезкам. В первую очередь, например, можно разбить исходный отрезок интегрирования на [math]p[/math] частей, где [math]p[/math] - количество процессоров. Стоит отметить, что алгоритм сгущает сетку вокруг отрезков "малой гладкости" интегрируемой функции, так что только разбиения начального отрезка интегрирования, вообще говоря, недостаточно для эффективной работы параллельного алгоритма. Для решения данной проблемы можно организовать, например, стек, в котором хранятся еще не проинтегрированные отрезки. С данной точки зрения для параллельного алгоритма стоит воспользоваться схемой "мастер - рабочий".

1.9 Входные и выходные данные алгоритма

На вход алгоритму подается интегрируемая функция [math]f(x)[/math], заданной в виде формулы на отрезке [math][a,b][/math], и допустимая погрешность интегрирования [math]\varepsilon[/math]. Результатом работы алгоритма является приближенное значение [math]Q[/math] интеграла [math]\int\limits_a^b f(x)\,dx[/math].

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

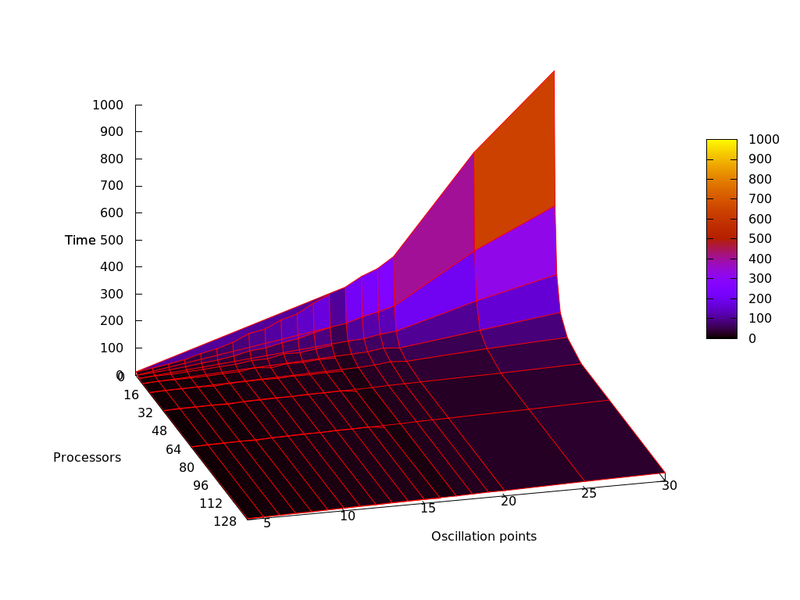
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. В качестве интегрируемой области был выбран отрезок [math][a,b] = [0,10][/math], допустимая погрешность интегрирования составляла [math]\varepsilon = 10^{-6}[/math], а интегрируемой функцией была [math]f_k(x) = \sum\limits_{i = 0}^{k-1} (x - x_i) * sin(\frac{1}{x - x_i})[/math], где [math]x_i = a + \frac{b-a}{2k} + i * \frac{b-a}{k}[/math]. В процессе тестирования менялось количество "особых" точек [math]k[/math] и число процессоров [math]p[/math]. Число процессоров выбиралось как [math]2^i[/math], [math]i = 0,1,..,7[/math]; количество "особых" точек - [math]4,5,..20,25,30[/math]. Ниже представлен график времени работы программы.

Рисунок 2. Параллельная реализация алгоритма адаптивного интегрирования

2.7 Существующие реализации алгоритма

Действительно широкого распространения, как, например, решение СЛАУ различными методами, данная задача не обрела. Тем не менее существует немало реализаций алгоритмов адаптивного интегрирования, например, таких как и .