Участник:Bormas

Название алгоритма: "Алгоритм генерирования случайных величин и построение статистики по заданной плотности распределения"

Автор описания: Гончаров Б.И., Постановка задачи: Пагурова В.И.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Постановка задачи: Пусть [math] X_1, X_2,...X_n [/math] - независимые одинаково распределенные случайные величины с общей функцией распределения [math] F(x) [/math], для которой при [math] x \to +\infty [/math] имеет место следующее представление:[math] F(x)=1-C(lnx)^{\beta-1}x^{-\alpha} [/math], где [math] C \gt 0 , \alpha \gt 0, \forall \beta [/math].

Методом статистического анализа показать, что [math] \lim_{n \to \infty}F(X_n^{(n)}) = \exp{x^{-\alpha}}, x \gt 0 [/math] и найти коэффициенты [math] a_n \gt 0 [/math].

Построить гистограмму статистики [math] T_n = \frac{X_n^{(n)}}{a_n} [/math] для функции [math] F(x) = 1 - \frac{2\sqrt{\ln{2}}}{(x+1)\sqrt{\ln{(x+1)}}}, x \gt 1 [/math] и сравнить её с функцией предельного распределения.

1) Сначала генерируем [math]n[/math] случайных величин [math] X_1, X_2,..., X_n [/math] из непрерывной функции распределения

2) Далее берем [math] X_n^{(n)} = X_n [/math], то есть максимально возможный элемент выборки из [math]n[/math] элементов

3) Затем делим [math] X_n^{(n)} [/math] на [math] a_k [/math], получая наш первый элемент статистики [math] \frac{X_n^{(n)}}{a_1} [/math]

4) Далее повторяем пункты 1) - 3) и генерируем столько статистик, сколько нам нужно. Чем больше статистик мы сгенерируем, тем более точная будет гистограмма

1.2 Математическое описание алгоритма

Обозначим за [math] \overline{F}(x) = 1 - F(x) [/math]

Рассмотрим [math] \frac{\overline{F}(tx)}{\overline{F}(x)} = \frac{C(\ln{tx})^{\beta-1}(tx)^{-\alpha} }{C(\ln{x})^{\beta-1}x^{-\alpha}} \to t^{-\alpha} [/math] при [math]x \to \infty [/math] [math] \Rightarrow [/math] [math] F(x) \in MDA(\Phi_\alpha)[/math], то есть принадлежит классу предельных распределений Фреше

Теперь найдем [math] a_n [/math]:

[math] \overline{F}(x) \sim C(\ln{x})^{\beta-1}x^{-\alpha}[/math] при [math]x \to \infty [/math], [math] \overline{F}(a_n) \sim \frac{1}{n}[/math] [math] \Rightarrow [/math]

[math] \ln{[C(lna_n)^{\beta-1}a_n^{-\alpha}]} = \ln{\frac{1}{n}}[/math]

[math] \ln{C} + (\beta-1)\ln{\ln{a_n}} - \alpha \ln{a_n} = -\ln{n}[/math]

[math] \alpha \ln{a_n} - (\beta-1)\ln{\ln{a_n}} - \ln{C} = \ln{n}[/math]

Будем искать [math] \ln{a_n} [/math] в виде: [math] \ln{a_n} = \frac{1}{\alpha}(\ln{n} + \ln{r_n})[/math], где [math] \ln{r_n} = \overline{O}(\ln{n})[/math]

[math] \ln{C} + (\beta-1)\ln{[\frac{1}{\alpha}(\ln{n} + \ln{r_n})]} - \ln{n} - \ln{r_n} = -\ln{n} [/math]

[math] \ln{r_n} \simeq \ln{C} - (\beta - 1)\ln{\alpha} + (\beta - 1)\ln{\ln{n}} = \ln{(C(\ln{n})^{\beta - 1}\alpha^{-(\beta - 1)})} [/math] - подставляем это в [math] \ln{a_n} [/math]

[math] \ln{a_n} \sim \frac{1}{\alpha}(\ln{n} + \ln{(C(\ln{n})^{\beta - 1}\alpha^{-(\beta - 1)})}) [/math]

[math] a_n = (\frac{Cn(\ln{n})^{\beta-1}}{\alpha^{\beta - 1}})^{\frac{1}{\alpha}}[/math]

В частном случае (из функции распределения):

[math] C = 2\sqrt{\ln{2}}; \alpha = 1; \beta = \frac{1}{2} [/math] - находятся путём подставления в [math] \overline{F}(a_nx) = \frac{2\sqrt{\ln{2}}}{(x + 1)\sqrt{\ln{(x + 1)}}} [/math]

[math] a_n = \frac{2\sqrt{\ln{2}}n}{\sqrt{\ln{n}}} [/math]

Из свойства класса распределений Фреше:

[math] P(X_n^{(n)} \lt xa_n) \to \begin{cases} e^{-\frac{1}{x}} &, x \gt 0 \\ 0 &, x \le 0 \end{cases} [/math]

[math] \Downarrow [/math]

[math] P(\frac{X_n^{(n)}}{a_n} \lt x) \to \begin{cases} e^{-\frac{1}{x}} &, x \gt 0 \\ 0 &, x \le 0 \end{cases} [/math] - предельная функция распределения статистики

А сама статистика [math] \frac{X_n^{(n)}}{a_k} [/math] находится следующим образом:

1) Сначала генерируем какое-то количество случайных величин [math] X_1, X_2,..., X_n [/math]

2) Далее берем [math] X_n^{(n)} = X_n [/math], то есть максимально возможный элемент выборки

3) Затем делим [math] X_n^{(n)} [/math] на [math] a_k [/math], получая наш первый элемент статистики [math] \frac{X_n^{(n)}}{a_1} [/math]

4) Далее повторяем пункты 1) - 3) и чем больше статистик мы сгенерируем, тем более точная будет гистограмма

Затем нам нужно сравнить гистограмму статистики с функцией предельного распределения.

1.3 Вычислительное ядро алгоритма

Для того, чтобы задача работала быстрее, имеет смысл создание каждого элемента статистики вынести на отдельные ядра. Самым трудоемким процессом является процесс создания случайной величины из наперед заданной функции распределения.

Алгоритм образования случайных чисел с непрерывным законом распределения ("Аппроксимация распределений" Пагуровой В.И):

Пусть [math] U [/math] означает случайную величину с равномерным законом распределения [math] U(0, 1), F(x) [/math] -абсолютно непрерывная ф.р., тогда величина [math] X = F^{-1}(U) [/math] имеет ф.р. [math] F(x) [/math]. Предполагается, что случайная величина изменяется в конечной области [math] (a,b). [/math] Если область бесконечна, то в вычислительных целях следует обрезать её, например, в точках [math] a [/math] и [math] b. [/math] Тогда случайная величина будет изменяться в этой конечной области.

Пусть требуется генерировать значения случайной величины [math] X [/math] с плотностью распределения [math] f(x), f(x) \gt 0 [/math] для [math] x \subseteq [a,b], f(x) = 0 [/math] для [math] x \nsubseteq [a,b].[/math] Обозначим [math] f = \max_{x \subseteq [a,b]}f(x). [/math] Образуем пару [math] (U_1, U_2), U_1 \sim U(0,1), U_2 \sim U(0,1). [/math] Вычисляем [math] X = a + (b - a)U_2. [/math] Если [math] U_1 \lt f(X)/f [/math], то принимаем [math] X [/math] в качестве требуемой случайной величины, в противном случае пару [math] (U_1, U_2) [/math] отбрасываем и все начинаем сначала. Метод основан на том факте, что если [math] U_1 \sim U(0,1), U_2 \sim U(0,1), U_1 [/math] и [math] U_2 [/math] независимы, тогда условная плотность распределения величины [math] a + (b - a)U_2 [/math] при условии [math] U_1 \lt f(a + (b - a)U_2)/f [/math] равна [math] f(x) [/math].

В нашей задача функция [math] f(x) = \frac{\sqrt{\ln{2}}(2\ln{(x + 1)} + 1)}{(x + 1)^2(\ln{(x + 1)})^{\frac{3}{2}}}, x \gt 1 [/math]

Сдвинем [math] x [/math] для удобства, таким образом: [math] f(x) = \frac{\sqrt{\ln{2}}(2\ln{(x + 2)} + 1)}{(x + 2)^2(\ln{(x + 2)})^{\frac{3}{2}}}, x \gt 0 [/math]

Эта функция невозрастающая, поэтому [math] f_{max} [/math] достигается при [math] x = 0 [/math], таким образом: [math] f_{max} = \frac{\sqrt{\ln{2}}(2\ln{(2)} + 1)}{(2)^2(\ln{(2)})^{\frac{3}{2}}} [/math]

Теперь у нас есть все необходимые данные для построения статистики [math] \frac{X_n^{(n)}}{a_k}. [/math]

1.4 Макроструктура алгоритма

Среди макроопераций данного алгоритма можно выделить обычные арифметические операции +-*/, операцию генерации случайного числа с равномерным законом распределения от 0 до 1, операции сравнения, возведения в степень, вычисление натурального логарифма, вычисление значения функции в некоторой точке и операцию смены контекста рандомизации (для каждого из процессов он свой). В последнем пункте имеется в виду следующее: функция rand() в языке С является псевдорандомной и для ее корректной работы нужно задавать seed, то есть начальное некоторое положительное число, настраивающее эту функцию. Это число необходимо сделать разным для каждого из процессов, так как в случае когда оно везде будет одинаково - у нас функция rand() будет возвращать одинаковые результаты на всех процессах, таким все процессы сгенерируют одинаковое число, что не является желаемым результатом работы программы.

Если более детально пройтись по пунктам поиска статистики [math] \frac{X_n^{(n)}}{a_k} [/math]:

1) Генерируем 2 числа [math] U_1, U_2 [/math] путем (double)rand()/(double)RAND_MAX; (seed мы уже заранее задали)

2) Ищем [math] x = a + (b - a)U_2 [/math]

3) Ищем [math] f(x) = \frac{\sqrt{\ln{2}}(2\ln{(x + 2)} + 1)}{(x + 2)^2(\ln{(x + 2)})^{\frac{3}{2}}} [/math]

4) Проверяем [math] U_1 \lt \frac{f(x)}{f_{max}}[/math], где [math]f_max[/math] - заранее посчитанная константа

5) Сравниваем [math] maxval \lt х [/math], где maxval - наибольший элемент статистики (изначально равный 0) Если условие выполнено, то [math] maxval = х [/math] и пункты 1-5 снова повторяются, пока мы не сгенерируем столько случайных величин, сколько мы задали.

6) Далее делим [math]maxval[/math] на [math] a_k = \frac{2\sqrt{\ln{2}}k}{\sqrt{\ln{k}}} [/math], где [math]k[/math] - номер процесса. [math]k = 1, 2, 3...[/math]

7) Пересылаем полученный результат нулевому процессу, отвечающему за сбор данных

8) После того, как нулевой процесс дождался всех данных - он записывает только те данные в массив, которые меньше [math]scale[/math]. (Это нужно для корректного масштабирования графика)

9) Далее происходит создание файла с нашими числами

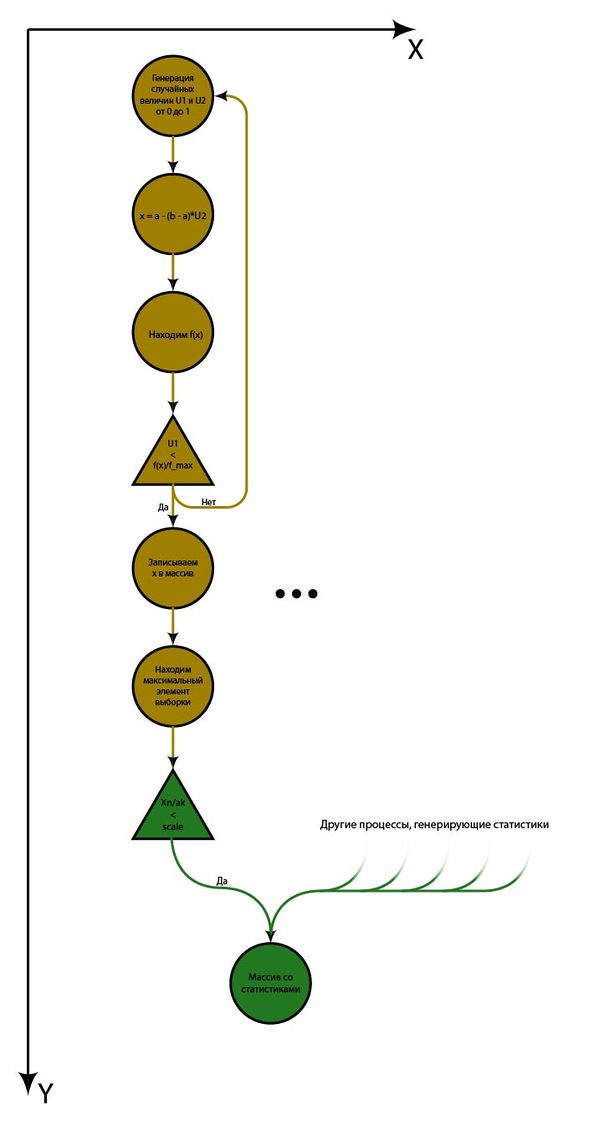
1.5 Схема реализации последовательного алгоритма

1) Генерируем 2 случайные величины [math] U_1, U_2 [/math] с равномерным законом распределения от 0 до 1

2) Задаем некоторый [math] x = a - (b - a)*U_2 [/math]

3) Находим [math] f(x) [/math]

4) Проверяем [math] U_1 \lt \frac{f(x)}{f_{max}} [/math], где [math] f_{max}[/math] - некоторая заранее известная константа

5) Если условие выполняется, то сравниваем [math] x [/math] c [math] maxval [/math], иначе повторяем пункты 1)-4) заново до тех пор, пока условие не выполнится

6) По окончании цикла имеем максимальный элемент выборки [math] X_n^{(n)} = maxval [/math]

7) Делим этот элемент на [math] a_k [/math], таким образом получая статистику [math] \frac{X_n^{(n)}}{a_k}[/math]

8) Заполняем массив статистик теми данными, которые входят в диапазон отрисовки графика, то есть удовлетворяющие условию [math] \frac{X_n^{(n)}}{a_k} \lt scale[/math].

1.6 Последовательная сложность алгоритма

Сложность алгоритма оценить невозможно, так как есть элемент случайности, из-за которого нельзя понять, сколько операций мы сможем совершить, прежде чем мы сгенерируем случайную величину. Иными словами, алгоритм имеет неоднородную сложность. Однако, если её условно усреднить.

Пусть [math]N[/math] - число статистик;

[math]M[/math] - усредненное число итераций до тех пор, пока одна статистика не будет сгенерирована;

[math]P[/math] - число случайных величин, необходимых для одной статистики;

• [math]2NMP[/math] генераций случайных величин [math]U_1, U_2[/math]
• [math]NMP[/math] вычислений значений параметра [math]x[/math]
• [math]NMP[/math] вычислений значений функции [math]f(x)[/math]
• [math]NMP[/math] сравнений
• [math]N[/math] вычислений [math]a_k[/math]
• [math]N[/math] делений
• [math]N[/math] сравнений со [math]scale[/math]

Таким образом, алгоритм является линейным относительно количества статистик и случайных величин, необходимых для одной статистики.

1.7 Информационный граф

1.8 Ресурс параллелизма алгоритма

Данный алгоритм для статистики размера [math] N [/math] и количества случайных величин [math] P [/math] работает в [math] NP [/math] раз быстрее чем последовательный, так как вычисление каждой статистики можно вынести в отдельный процесс, но при слишком большой выборке "узким горлышком" системы может оказаться первый процесс, который принимает все сообщения от других процессов, но эта задержка так незначительна, что ей можно пренебречь.

• 1 ярус вычислений вычисление случайных величин [math]O(NP)[/math].
• 1 ярус делений на [math]a_k[/math] ([math]O(N)[/math]);
• 1 ярус сравнений со [math]scale[/math] ([math]O(N)[/math]).

При классификации по высоте ярусно-параллельной формы алгоритм генерирования статистик имеет сложность 4. При классификации по ширине его сложность будет [math]O(NP)[/math].

1.9 Входные и выходные данные алгоритма

Для нашей программы нужно ввести 2 параметра. N - количество случайных величин для каждой статистики T - количество статистик. По сути это число равно количеству процессов + 1, которые нужно запустить на машине чтобы получить T статистик

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Так как фиксированной вычислительной сложности установить невозможно, то обозначим усредненную за [math] W [/math]. И сильная и слабая масштабируемости почти линейно зависят от количества параллельно запущенных процессов, ведь каждый процесс независимо от других производит одноразовую генерацию случайных величин, которые затем поступают на аккамулирующий процесс(см. схему) для образования файла со статистиками.

Были произведены запуски на суперкомпьютере Ломоносов с количеством ядер 64, 128, 256, 512 и 1024. И время выполнения в среднем возрастало но незначительно.

Как уже говорилось, издержки могут быть вызваны большим количеством информации передаваемое аккамулирующему процессу, но эти издержки столь незначительны, что ими можно пренебречь. Тем более в данной задачи имеет смысл рассматривать не более 2000 статистик, поэтому такое количество процессов смогут быстро передать результаты "слушающему" процессу.

Порой даже бывало, что процесс с числом процессов 256 отработает быстрее, чем 64. Это связано с тем, что данный алгоритм зависит от того, какие значения выдаст функция rand(), которые далее должны пройти через условие. Если они не удовлетворяют некоторому условию, то процесс повторяется заново до того момента, пока условие не выполнится. Таким образом увеличение количества процессов увеличивает шанс того, что какая-то из статистик будет долго генерировать случайную величину.

2.7 Существующие реализации алгоритма

На своей практике мною подобные алгоритмы встречены не были

3 Литература

Курс лекций от Sharcnet HPC [[1]]

"Аппроксимация распределений" Пагурова В.И.