Участник:Сорокин Александр/Метод сопряженных градиентов (Решение СЛАУ)

Метод сопряженных градиентов для решения СЛАУ. Сорокин Александр 403

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод сопряженных градиентов представляет собой итерационный метод для численного решения системы уравнений с симметричной и положительно определенной матрицей, является итерационным методом Крыловского типа. Основная идея метода заключается в том, чтобы минимизировать на подпространствах Крылова А-норму ошибки.

1.2 Математическое описание алгоритма

Пусть необходимо найти решение системы уравнений [math] Ax = b [/math], где [math] A^T = A \gt 0 [/math].
Рассмотрим функционал [math] \phi (x) = \frac{1}{2}x^T A x - x^T b [/math].
Если [math] x^* [/math] это решение задачи минимизации данного функционала, то в этой точке градиент [math] \bigtriangledown \phi (x^*) = Ax^* - b [/math] должен быть равен нулю. Таким образом, минимизируя функционал [math] \phi (x) [/math] мы получим решение исходной системы.

1.2.1 Метод градиентного спуска

Как известно, градиент [math] \bigtriangledown \phi (x) [/math] является направлением наибольшего роста функции.
Метод градиентного спуска основан на стратегии движения в строну, противоположную возрастанию функционала. Оптимальным направлением в этом случае будет антиградиент [math] -\bigtriangledown \phi (x) [/math] и двигаться по нему нужно будет до тех пор, пока функционал убывает.
Таким образом можно построить следующий итерационный метод:

1. Выберем произвольное начальное приближение [math] x_0 [/math].
2. [math] x_{i+1} = x_{i} + \alpha_i p_i [/math], где [math] p_i [/math] — направление движения, а [math] \alpha_i [/math] — величина шага.
   

Из рассуждений выше понятно что оптимальным является направление [math] p_i = - \bigtriangledown \phi (x_{i}) = b - Ax_i = r_i [/math]. Величина [math] \alpha_i [/math] выбирается из соображений [math] \alpha_i = \underset{\alpha}{\operatorname{argmin}} \phi (x_i + \alpha p_i) [/math]. Аналитическую формулу [math] \alpha_i = \frac{\bigtriangledown\phi (x_i)^T \bigtriangledown\phi (x_i)}{\bigtriangledown\phi (x_i)^T A \bigtriangledown\phi (x_i)} = \frac{r_i ^T r_i}{r_i ^T A r_i} = \frac{p_i ^T r_i}{p_i ^T A p_i} [/math] можно получить из [math] \frac{d}{d\alpha} \phi (x_i + \alpha p_i) = 0 [/math].

1.2.2 Метод сопряженных направлений

Метод градиентного спуска обычно сходится очень долго. Можно построить алгоритм который сходится не больше чем за n шагов.
Предположим что у нас есть n линейно-независимых векторов [math] p_1, ... p_n [/math] таких что [math] (p_i, p_j)_A = (Ap_i, p_j) = 0, i \neq j [/math].
Так как имеется n таких векторов, то они образуют базис пространства и любой вектор можно выразить через них, в том числе [math] x^* - x_0 = \sum_{i = 1}^n \alpha_i p_i [/math].
Домножим это равенство А-скалярно на [math] p_k [/math] для всех k. С левой стороны получим [math] (x^* - x_0, p_k)_A = (b - Ax_0, p_k) = p_k ^T r_0 [/math]. С правой: [math] \sum_{i = 1}^n \alpha_i (p_i, p_k)_A = \alpha_k (p_k, p_k)_A = \alpha_k p_k ^T A p_k [/math]. Тем самым [math] \alpha_k = \frac{p_k^T r_0}{p_k^T A p_k} [/math].
Итак мы получили новый алгоритм решения:

1. Выбираем начальное приближение [math] x_0 [/math] и А-ортогональные направления [math] p_1, ..., p_n [/math].
2. Для всех [math] k = 1, ... n [/math]:
   1. Выбираем [math] \alpha_k = \frac{p_k^T r_0}{p_k^T A p_k} [/math].
   2. Обновляем [math] x_{k+1} = x_{k} + \alpha_k p_k [/math].

Таким образом получим [math] x_{n} = x^* [/math].
Кроме того, стоит обратить внимание на следующий факт: [math] p_k^T r_0 = p_k^T(b - Ax_0) = p_k^T(b - A[x_0 + \alpha_1 p_1 + ... + \alpha_{k-1} p_{k-1}]) = p_k^T r_k [/math], тем самым формула для [math] \alpha_k [/math] в этом методе совпадает с формулой в методе градиентного спуска.

1.2.3 Метод сопряженных градиентов

Метод сопряженных градиентов это частный случай метода сопряженных направлений.
В этом методе мы будем искать новое приближение для решения [math] x [/math] и новый вектор направления [math] p [/math]. Новый вектор направления будем получать используя алгоритм Грамма-Шмидта, где в качестве начальной линейно-независимой системы будем использовать невязки [math] r_i [/math]. Метод будет выглядеть так:

1. Выбираем начальное приближение [math] x_0 [/math]. Вычисляем невязку и вектор направления [math] r_0 = b - Ax_0, p_0 = r_0 [/math].
2. Для [math] k = 0, 1, 2 ... [/math] и до тех пор пока итерационный процесс не сойдется:
   1. Вычисляем [math] \alpha_k = \frac{p_k^T r_k}{p_k^T A p_k} = \frac{r_k^T r_k}{p_k^T A p_k} [/math]
   2. Новое приближение [math] x_{k + 1} = x_{k} + \alpha_k p_k [/math]
   3. Новая невязка [math] r_{k + 1} = r_{k} - \alpha_k A p_k [/math]
   4. Вычисляем [math] \beta_k = -\frac{p_k^T A r_{k+1}}{p_k^T A p_k} = \frac{r_{k + 1}^T r_{k+1}}{r_k^T r_k} [/math]
   5. Новый вектор направления [math] p_k = r_{k+1} + \beta_k p_k [/math]

Последние два пункта алгоритма описывают процесс ортогонализации. Соотношения получились «короткими» в силу того, что [math] p_j^T Ar_{k+1} = 0, j \lt k [/math].

1.3 Вычислительное ядро алгоритма

Основную часть алгоритма составляют операции умножения матрицы на вектор [math]Ap_k[/math], вычисления скалярных произведений [math](r_k, r_k)[/math], [math](Ap_k, p_k)[/math], [math](r_{k+1}, r_{k+1})[/math], а так же операции обновления векторов [math] x_k [/math], [math]r_k[/math], [math]p_k[/math].

1.4 Макроструктура алгоритма

На каждой итерации алгоритма вычисляются:

1. 3 cкалярных произведения векторов
2. 3 обновления вектора
3. 1 умножение матрицы на вектор

1.5 Схема реализации последовательного алгоритма

Вычислить [math] r_0 =b - Ax_0 [/math] для некоторого начального [math] x_0 [/math].
[math] p_0 = r_0 [/math]
Для [math] k = 0, 1, 2 ... [/math]
[math] \alpha_k = (r_k, r_k) / (p_k, Ap_k) [/math]
[math] x_{k + 1} = x_k + \alpha_k p_k [/math]
[math] r_{k + 1} = r_k - \alpha_k A p_k [/math]
[math] \beta_k = (r_{k+1}, r_{k+1}) / (r_k, r_k) [/math]
[math] p_{k+1} = r_{k+1} + \beta_k p_k [/math]
Проверить условие сходимости; продолжить если необходимо
Конец

1.6 Последовательная сложность алгоритма

Рассмотрим сложность каждой итерации:
Вычисление скалярного произведения требует [math] n [/math] операций умножения и [math] n - 1 [/math] операцию сложения. Общая сложность — [math] 2n - 1 [/math] операций.
Обновление вектора требует [math] n [/math] операций умножения и [math] n [/math] операций сложения. Итого — [math] 2n [/math] операций.
Умножение матрицы на вектор эквивалентно вычислению [math] n [/math] скалярных произведений. Следовательно, необходимо выполнить [math] n(2n-1) = 2n^2 - n [/math] операций.
Таким образом, на каждой итерации необходимо выполнить [math] 3 \times (2n - 1) + 3 \times (2n) + (2n^2 - n) = 2n^2 + 11n - 3 = O(n^2) [/math] операций.
Общая сложность алгоритма — [math] O(In^2) [/math] , где [math] I \le n [/math] — число итераций.

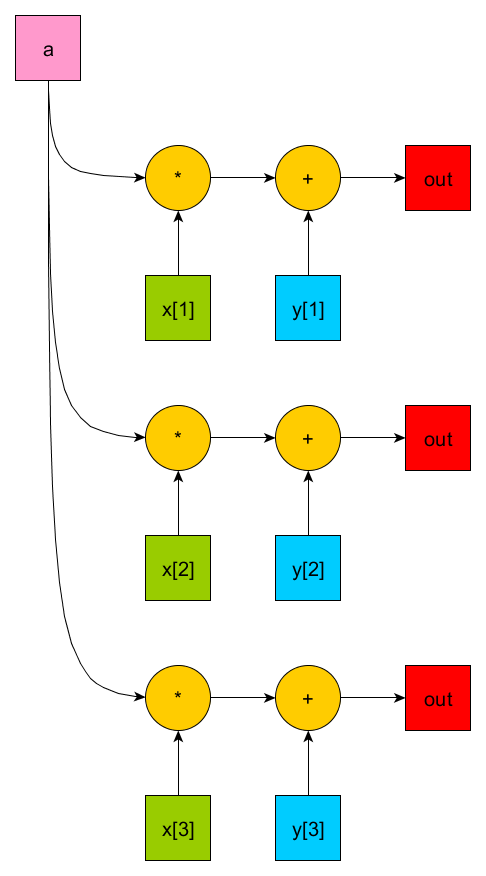
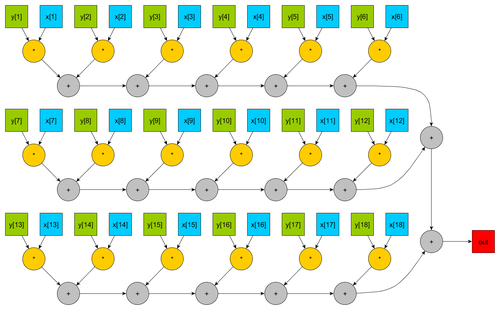
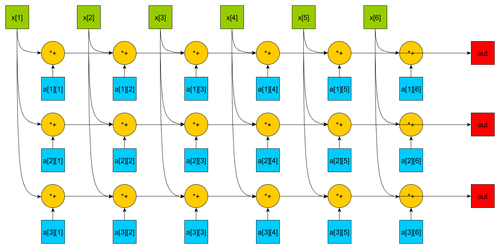
1.7 Информационный граф

Основным ресурсом параллелизма будут являться обновление вектора, вычисление скалярного произведения, умножение матрицы на вектор. Представим информационные графы для данных алгоритмов:

Рисунок 1. Граф последовательного обновления вектора с отображением входных и выходных данных

Рисунок 2. Граф последовательного-параллельного вычисления скалярного произведения векторов с отображением входных и выходных данных

Рисунок 3. Граф последовательного умножения плотной матрицы на вектор с отображением входных и выходных данных

1.8 Ресурс параллелизма алгоритма

Большую часть времени работы алгоритма занимает выполнение операций умножения матрицы на вектор, вычисления скалярного произведение двух векторов и операции обновления вектора. Эти операции легко поддаются распараллеливанию, что позволяет ускорить процесс вычисления.

Эти вычислительные задачи можно разбить на две группы: операции типа матрица-вектор и вектор-вектор.

К первой группе относится операция умножения матрицы на вектор. Для ее параллельного вычисления матрица разбивается на горизонтальные блоки равного размера, количество которых равно числу используемых процессоров. Кроме того на каждом процессоре должна находиться полная копия умножаемого вектора.

Ко второй группе относятся операции вычисления скалярного произведения двух векторов и операция обновления вектора. Для их вычисления вектора также разбиваются на блоки равного размера, после чего каждый процессор может вычислить требуемую операцию с «укороченными векторами».

Параллельное вычисление операций обоих групп подразумевает, что в результате вычислений на каждом процессоре будет находится лишь часть результата. Поэтому после выполнения вычислений необходимо произвести операцию сбора данных.

1.9 Входные и выходные данные алгоритма

Входные данные:

Положительно определенная матрица [math]A\in \mathbb{R}^{n\times n}[/math] коэффициентов СЛАУ.

Вектор правой части [math]b\in \mathbb{R}^{n}[/math].

Опционально:

Требуемая точность [math] \varepsilon \gt 0 [/math].

Предельно допустимое число итераций [math] i_{max} [/math].

Выходные данные:

Вектор [math]x \in \mathbb{R}^{n}[/math] — решение СЛАУ.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости параллельной реализации метода проводилось на суперкомпьютере "Ломоносов" cуперкомпьютерного комплекса МГУ им. Ломоносова.
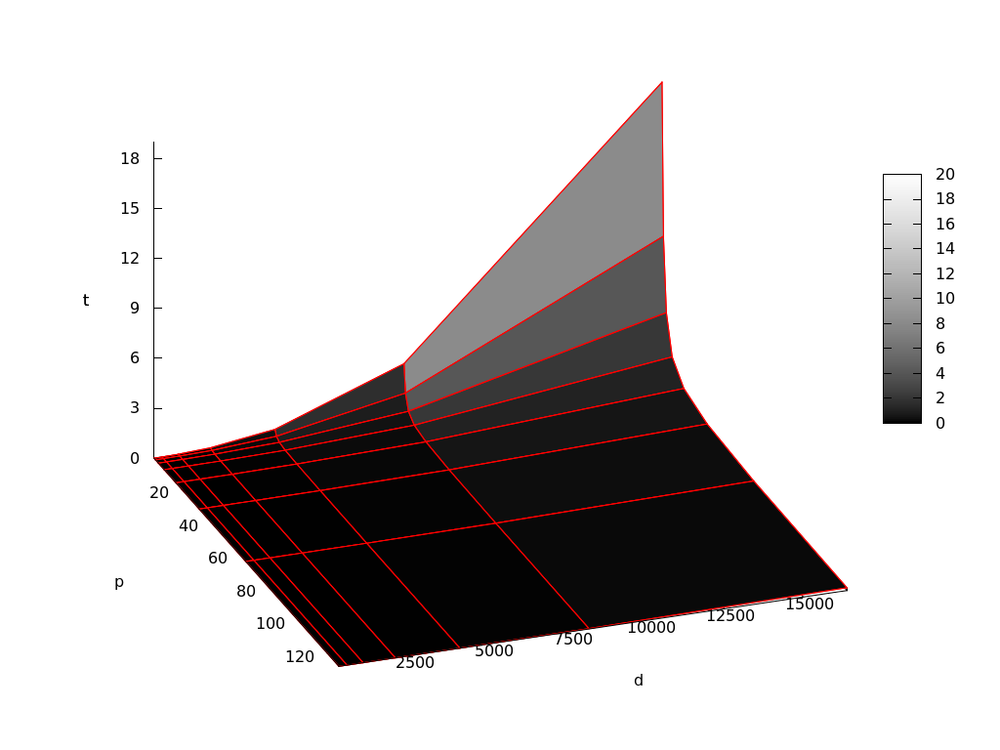
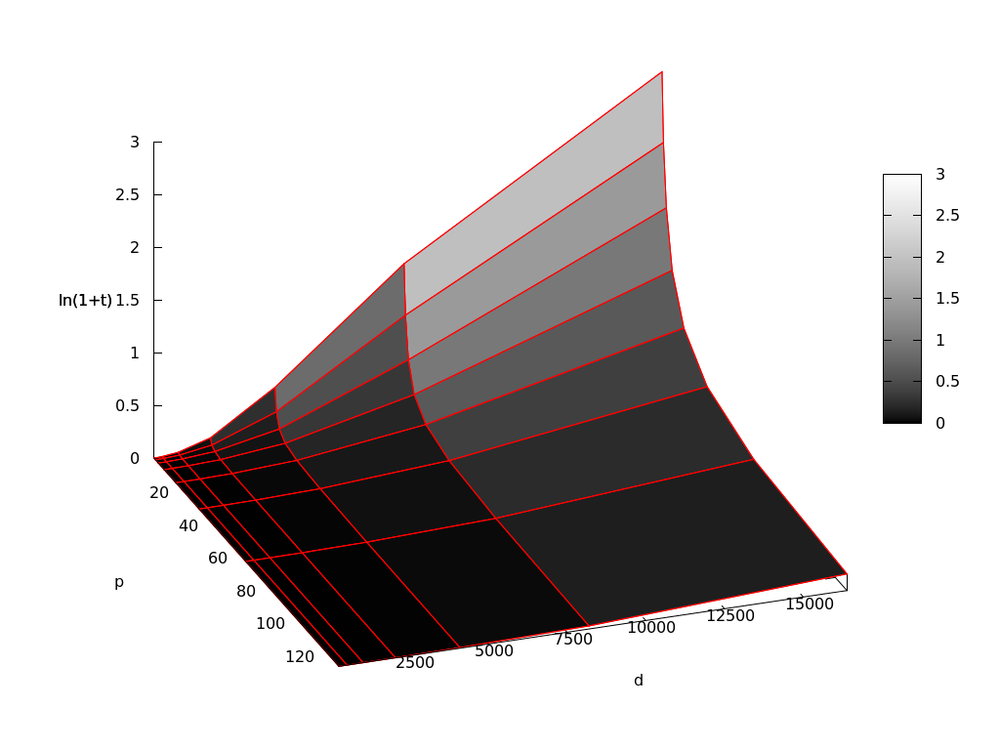
Была написана программа для параллельного решения СЛАУ с использованием метода сопряженных градиентов. В процессе тестирования программы изменялись [math]d[/math] — порядок системы, [math]p[/math] — число используемых процессоров. Число обусловленности системы оставалось неизменным и равным [math]10000[/math]
Число процессоров выбиралось как [math]2^i[/math], [math]i = 0,1,..,7[/math]; порядок матрицы — [math]2^k[/math], [math]k = 8,..,14[/math].
Ниже представлены графики времени [math]t[/math] работы программы:

• 

  Время работы программы в минутах

• 

  Логарифмическая версия для большей наглядности

Программа компилировалась при помощи команды mpicc -std=c99 main.c -o cg -lm
Запускалась: ./cg d 10000 , где [math]d[/math] — размерность системы.

2.7 Существующие реализации алгоритма

Метод сопряженных градиентов реализован в большом числе вычислительных пакетов. Приведем наиболее популярные из них:

• LAPACK
• Intel MKL
• SPARSKIT
• Matlab
• SciPy

3 Литература

• Методы численного анализа Евгений Евгеньевич Тыртышников
• An Introduction to the Conjugate Gradient Method Without the Agonizing Pain by Jonathan Richard Shewchuk
• Iterative methods for sparse linear systems by Yousef Saad
• Notes on Some Methods for Solving Linear Systems by Dianne P. O'Leary