Уравнение Пуассона, решение дискретным преобразованием Фурье

Основные авторы описания: В.М.Степаненко, Е.В.Мортиков

Содержание

1 Свойства и структура алгоритма
2 Программная реализация алгоритма
3 Литература
4 Свойства и структура алгоритма
5 Программная реализация алгоритма
6 Литература

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Уравнение Пуассона для многомерного пространства имеет вид:

[math] \begin{equation} \label{eq:poisson} \sum_{i=1}^{N}\frac{\partial^2 \phi}{\partial x_i^2}=f,~\mathbf{x}\in D, \end{equation} [/math]

где [math]D \in \mathbb{R}^N[/math] - область определения решения [math]\phi(\mathbf{x})[/math], [math]\mathbf{x}=(x_1,...,x_N)^T[/math] - вектор независимых переменных. Уравнение Пуассона дополняется граничными условиями:

[math] \begin{equation} B(\phi)=F,~ \text{на}~ \mathbf{x}\in \Gamma(D), \end{equation} [/math]

где [math]\Gamma(D)[/math] - граница области [math]D[/math], a [math]B(\phi)[/math] - оператор, определяющий граничные условия. [math]B(\phi)=\phi[/math] соответствует граничным условиям Дирихле, [math]B(\phi)=\partial\phi/\partial n[/math] ([math]\mathbf{n}[/math] - внешняя нормаль к границе [math]\Gamma(D)[/math]) - условиям Неймана. Иногда задают также смешанное граничное условие: [math]B(\phi)=С\phi+\partial\phi/\partial n[/math] ([math]C[/math] - константа). Встречаются также так называемые "периодические граничные условия", при которых задача ставится для бесконечной области, но предполагается периодичность решения по подмножеству переменных из [math]\mathbf{x}[/math].

Уравнение Пуассона возникает во многих задачах математической физики, например, в электростатике (в этом случае [math]\phi[/math] - потенциал электрической силы) и гидродинамике ([math]\phi[/math] - давление жидкости или газа); при этом [math]N=2,3[/math] для плоской и трехмерной задач, соответственно.

Решение уравнения Пуассона для произвольной правой части и неоднородных граничных условий в аналитическом виде неизвестно, поэтому в большинстве приложений оно находится численно. Наиболее распространенная дискретизация уравнения имеет вид

[math] \begin{equation} \sum_{i=1}^{N}\frac{\phi_{k_1,...,k_i+1,...,k_N}-2\phi_{k_1,...,k_i,...,k_N}+\phi_{k_1,...,k_i-1,...,k_N}}{\Delta x_i^2}=f_{k_1,...,k_N},~(k_1,...,k_N) \in D_N. \end{equation} [/math]

Здесь вторые производные заменены разностной аппроксимацией второго порядка точности (образуя т.н. схему "крест" для плоской задачи), а решение ищется на дискретном множестве точек [math]N[/math]-мерного пространства, [math]D_N[/math]. Конечными разностями аппроксимируются при этом также граничные условия.

1.2 Математическое описание алгоритма

В настоящей статье мы рассмотрим конечно-разностную схему для наиболее часто встречающейся задачи решения уравнения Пуассона в трехмерном пространстве:

[math] \begin{equation} \label{eq:poisdiscr} \frac{\phi_{i+1,j,k}-2\phi_{i,j,k}+\phi_{i-1,j,k}}{ \Delta x^2} + \frac{\phi_{i,j+1,k}-2\phi_{i,j,k}+\phi_{i,j-1,k}}{ \Delta y^2} + \frac{\phi_{i,j,k+1}-2\phi_{i,j,k}+\phi_{i,j,k-1}}{ \Delta z^2} = f_{i,j,k},~(i,j,k) \in D_h, \end{equation} [/math]

где [math]D_h=\{0:N_x-1\}\times\{0:N_y-1\}\times\{0:N_z-1\} [/math] - параллелепипед в сеточной области. В качестве граничных условий для простоты примем так называемые троякопериодические граничные условия

[math] \begin{align} \phi_{0,j,k}=\phi_{N_x,j,k},\\ \phi_{i,0,k}=\phi_{i,N_y,k},\\ \phi_{i,j,0}=\phi_{i,j,N_z}. \end{align} [/math]

Периодические граничные условия удовлетворяются "автоматически", если представить решение в виде стандартного дискретного обратного преобразования Фурье:

[math] \begin{equation} \label{eq:fourier} \phi_{i,j,k}=\frac{1}{N_x N_y N_z}\sum_{l=0}^{N_x-1}\sum_{m=0}^{N_y-1}\sum_{n=0}^{N_z-1}\Phi_{l,m,n}e^{2\pi \overline{i} \left(\frac{il}{N_x}+\frac{jm}{N_y}+\frac{kn}{N_z}\right)}. \end{equation} [/math]

Здесь [math]\overline{i}=\sqrt{-1}[/math]. Аналогичное разложение применяется также к правой части уравнения, [math]f_{i,j,k}[/math]. Решение дисретного уравнения Пуассона преобразованием Фурье удобно тем, что базисные функции разложения Фурье являются собственными функциями дискретного оператора Лапласа. А именно, подставляя разложение Фурье неизвестной функции [math]\phi_{i,j,k}[/math] и правой части в исходное уравнение, получаем:

[math] \begin{equation} \Phi_{l,m,n}=-\frac{F_{l,m,n}}{4\left[\sin^2\left(\frac{\pi l}{N_x}\right) + \sin^2\left(\frac{\pi m}{N_y}\right) + \sin^2\left(\frac{\pi n}{N_z}\right) \right]}. \end{equation} [/math]

где [math]F_{l,m,n}[/math] - преобразование Фурье правой части. Отсюда очевиден алгоритм решения уравнения: сначала правая часть уравнения разлагается в ряд Фурье, затем по приведенной выше формуле вычисляются коэффициенты Фурье решения и, наконец, решение восстанавливается обратным преобразованием Фурье.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является одномерное преобразование Фурье. В самом деле, обратное дискретное преобразование Фурье может быть записано как

[math] \begin{equation} \label{eq:fourier2} \phi_{i,j,k}=\frac{1}{N_x} \sum_{l=0}^{N_x-1} \left[ e^{2\pi \overline{i}\left(\frac{il}{N_x}\right)} \frac{1}{N_y} \sum_{m=0}^{N_y-1} \left[ e^{2\pi \overline{i}\left(\frac{jm}{N_y}\right)} \frac{1}{N_z} \sum_{n=0}^{N_z-1} \Phi_{l,m,n}e^{2\pi \overline{i} \left(\frac{kn}{N_z}\right)}\right]\right], \end{equation} [/math]

откуда видно, что трехмерное преобразование Фурье сводится в последовательности трех одномерных. Для вычисления одномерного преобразования широко используется эффективный алгоритм быстрого преобразования Фурье (FFT, Fast Fourier Transform)^[1].

1.4 Макроструктура алгоритма

Из приведенного выше ясно, что основной макрооперацией алгоритма решения уравнения Пуассона является одномерное быстрое преобразование Фурье. В дальнейшем будем обозначать ее [math]\text{FFT}_i,~i=x,y,z[/math] по каждому из трех направлений, соответственно, а обратное преобразование Фурье - [math]\text{IFFT}_i,~i=x,y,z[/math].

1.5 Схема реализации последовательного алгоритма

Введем для краткости следующие обозначения сеточных функций [math]\phi_h=\{\phi_{i,j,k},~(i,j,k) \in D_h\},~F_h=\{F_{l,m,n},~l=0,...,N_x-1,~m=0,...,N_y-1,~n=0,...,N_z-1\}[/math] и аналогично [math]f_h[/math] и [math]\Phi_h[/math]. Тогда алгоритм запишется следующим образом:

Вычисление [math]\text{FFT}_x(f_h)[/math]
Вычисление [math]\text{FFT}_y(\text{FFT}_x(f_h))[/math]
Вычисление [math]\text{FFT}_z(\text{FFT}_y(\text{FFT}_x(f_h)))=F_h[/math]
Расчет [math]\Phi_h[/math] по [math]F_h[/math]
Вычисление [math]\text{IFFT}_x(\Phi_h)[/math]
Вычисление [math]\text{IFFT}_y(\text{IFFT}_x(\Phi_h))[/math]
Вычисление [math]\text{IFFT}_z(\text{IFFT}_y(\text{IFFT}_x(\Phi_h)))=\phi_h[/math]

Примечательно, что весь описанный алгоритм реализуется с помощью одного трехмерного массива [math]N_x \times N_y \times N_z[/math], поскольку результат каждого одномерного преобразования Фурье можно записать во входной массив и затем использовать его на вход для следующего преобразования, а операция (4) - это поэлементное изменение массива.

1.6 Последовательная сложность алгоритма

Рассмотрим случай куба, [math]N_x=N_y=N_z=N=2^k[/math]. Тогда сложность одномерного БПФ по каждому из направлений составляет [math]N(\text{log}_2 N)[/math] операций. Поскольку одномерное БПФ на каждом этапе алгоритма осуществляется [math]N^2[/math] раз, таких этапов 6, а количество операций на этапе 4 составляет [math]N^3[/math], то общее количество действий составляет [math]N^3(6\text{log}_2 N+1)[/math].

1.7 Информационный граф

Информационный граф алгоритма представим для этапов 1-4, поскольку этапы 5-7 реализуются аналогично этапам 1-3.

Зеленые прямоугольники обозначают одномерные сечения входного трехмерного массива. Красным кругом обозначена операция одномерного БПФ, например [math]FFT_{x11}[/math] означает БПФ вдоль оси x при [math]j=1,~k=1[/math]. Желтыми кругами представлены поэлементные преобразования массива для получения коэффициентов Фурье решения (этап 4 алгоритма), например [math]L_{2N,1,...,N}[/math] означает преобразование элементов [math]i=2,~j=N,~k=1,...,N[/math]. Целочисленные индексы для краткости записи перенумерованы от [math]0,...,N-1[/math] до [math]1,...,N[/math]

Информационная зависимость между ярусами графа заключается в том, что одномерное БПФ зависит от результата произведенного ранее БПФ по перпендикулярному направлению (т.е. с предыдущего яруса), только если обрабатываемые этими БПФ одномерные сечения массива пересекаются. Следовательно, каждое из БПФ по второй координате, [math]FFT_{i,y,k},~i=1,...,N[/math] зависит от результатов каждого БПФ по первой координате [math]FFT_{x,j,k},~j=1,...,N[/math], и только от них, если эти преобразования производятся в одной плоскости [math]k=K[/math]. Соответственно, каждое БПФ по третьей координате [math]FFT_{i,j,z},~j=1,...,N[/math] зависит от каждого БПФ по второй [math]FFT_{i,y,k},~k=1,...,N[/math] в одной плоскости [math]i=I[/math].

1.8 Ресурс параллелизма алгоритма

В описанном выше алгоритме можно выделить, по меньшей мере, два уровня параллелизма. Во-первых, вычисление каждого одномерного БПФ может быть распределено между вычислительными ядрами. И, во-вторых, на каждом этапе алгоритма (ярусе графа) одномерные БПФ независимы друг от друга и также могут быть выполнены паралельно (координатный параллелизм). Для сопоставления параллельной (при координатном распараллеливании) и последовательной сложности алгоритма определим в качестве основных операций одномерное БПФ и поэлементный перерасчет массива (этап 4 алгоритма). Тогда последовательный алгоритм будет состоять из последовательно выполняемых [math]6N^2[/math] одномерных БПФ и [math]N^3[/math] операций над отдельными элементами массива, параллельный же алгоритм будет выполнен за 6 шагов одномерного БПФ и 1 операцию поэлементного преобразования. Если же выразить введенные макрооперации через элементарные арифметические опрации, то получим, что сложность последовательного алгоритма - [math]6N^3(\text{log}_2N)+N^3[/math], а сложность параллельного - [math]6N(\text{log}_2N)+1[/math]. Тогда при больших [math]N[/math] отношение последовательной сложности к параллельной стновится [math]\propto N^2(6\text{log}_2N \text{ln}2+\text{ln}2+5)[/math].

1.9 Входные и выходные данные алгоритма

В качестве входных данных выступает трехмерный массив [math]N \times N \times N[/math] правой части уравнения. Выходной массив - трехмерный массив решения той же размерности.

1.10 Свойства алгоритма

Как было показано выше, при неограниченном количестве вычислительных устройств и больших объемах входных данных вычислительная сложность параллельного алгоритма падает быстрее, чем [math]N^2[/math].

Поскольку объем входных данных составляет [math]N^3[/math], вычислительная мощность последовательного алгоритма становится [math]6\text{log}_2N+1[/math], а параллельного алгоритма - [math]\frac{6N\text{log}_2N+1}{N^3} \propto N^{-2}[/math] (при больших [math]N[/math]).

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Приведем пример реализации алгоритма на языке Фортран-90 с применением библиотеки FFTW. В этом случае трехмерное прямое преобразование Фурье правой части уравнения реализуется как последовательность трех одномерных (этапы 1-3 в п.1.5). Полученные коэффициенты Фурье делятся на собственное число оператора Лапласа (этап 4 в п.1.5) (см. комментарии в коде):

         ! x - transform
         do k = 1, k1
           do j = 1, j1
             workfor_x(1:i1) = cmplx(f_r(1:i1,j,k),f_i(1:i1,j,k))
             call FFTW_EXECUTE_DFT(planfor_x,workfor_x,workfor_x)
             f_r(1:i1,j,k) = real(real (workfor_x(1:i1)) )
             f_i(1:i1,j,k) = real(aimag(workfor_x(1:i1)) )
           enddo
         enddo
         ! y - transform
         do k = 1, k1
           do i = 1, i1
             workfor_y(1:j1) = cmplx(f_r(i,1:j1,k),f_i(i,1:j1,k))
             call FFTW_EXECUTE_DFT(planfor_y,workfor_y,workfor_y)
             f_r(i,1:j1,k) = real(real (workfor_y(1:j1)) )
             f_i(i,1:j1,k) = real(aimag(workfor_y(1:j1)) )
           enddo
         enddo
         ! z - transform and dividing by eigenvalue
         do j = 1, j1
           do i = 1, i1
             workfor_z(1:k1) = cmplx(f_r(i,j,1:k1),f_i(i,j,1:k1))
             call FFTW_EXECUTE_DFT(planfor_z,workfor_z,workfor_z)
             f_r(i,j,1:k1) = real(real (workfor_z(1:k1)) )
             f_i(i,j,1:k1) = real(aimag(workfor_z(1:k1)) )
             ! Dividing by eigenvalue of Laplace operator
             f_r(i,j,1:k1) = f_r(i,j,1:k1)/(sinx(i)+siny(j)+sinz(1:k1))
             f_i(i,j,1:k1) = f_i(i,j,1:k1)/(sinx(i)+siny(j)+sinz(1:k1))
           enddo
         enddo

Как только коэффициенты Фурье решения найдены, аналогично производится обратное преобразование Фурье:

         ! inverse x - transform
         do k = 1, k1
           do j = 1, j1
             workback_x(1:i1) = cmplx(f_r(1:i1,j,k),f_i(1:i1,j,k))
             call FFTW_EXECUTE_DFT(planback_x,workback_x,workback_x)
             f_r(1:i1,j,k) = real(real (workback_x(1:i1)) )/real(i1)
             f_i(1:i1,j,k) = real(aimag(workback_x(1:i1)) )/real(i1)
           enddo
         enddo
         ! inverse y - transform
         do k = 1, k1
           do i = 1, i1
             workback_y(1:j1) = cmplx(f_r(i,1:j1,k),f_i(i,1:j1,k))
             call FFTW_EXECUTE_DFT(planback_y,workback_y,workback_y)
             f_r(i,1:j1,k) = real(real (workback_y(1:j1)) )/real(j1)
             f_i(i,1:j1,k) = real(aimag(workback_y(1:j1)) )/real(j1)
           enddo
         enddo
         ! inverse z - transform
         do j = 1, j1
           do i = 1, i1
             workback_z(1:k1) = cmplx(f_r(i,j,1:k1),f_i(i,j,1:k1))
             call FFTW_EXECUTE_DFT(planback_z,workback_z,workback_z)
             f_r(i,j,1:k1) = real(real (workback_z(1:k1)) )
             f_i(i,j,1:k1) = real(aimag(workback_z(1:k1)) )
           enddo
         enddo

Как видим, вложенность циклов соответствует порядку расположения элементов массивов в Фортране - по столбцам - это позволяет существенно сократить время обращения к памяти. Многократно используются одни и те же вспомогательные массивы, что при небольших размерах сетки должно обеспечить быстроту работы с кэш-памятью. Однако, данная реализация не является оптимальной. Так, вместо многократного вызова подпрограммы FFTW_EXECUTE_DFT в циклах, можно было бы обращаться к одной подпрограмме, выполняющей заданное множество одномерных БПФ.

В приведенных выше листингах очевиден также и параллелизм алгоритма: каждое одномерное преобразование Фурье выполняется независимо. Самым простым способом использования этого обстоятельства будет вставка соответствующих директив OpenMP перед внутренними циклами - в случае использования ядер на общей памяти. В случае же параллельного выполнения на кластерах с распределенной памятью, небоходимо будет позаботиться о распределении входного массива (правой части уравнения) между процессорами, а также "транспозиции" массивов при переходе от БПФ по одному направлению к БПФ по следующему.

Заметим также, что в приведенной выше реализации для расчета одномерного БПФ производится вызов процедуры библиотеки FFTW, обрабатывающей массив комплексных чисел. В то же время, существует вариант БПФ для преобразования действительных массивов, ускоряющий БПФ в два раза (более подробно см. на сайте проекта FFTW).

Важным обстоятельством является то, что большинство вариантов БПФ, включая алгоритм Кули-Тьюки, в арифметике с плавающей запятой имеют очень низкую погрешность. Верхняя граница относительной ошибки для алгоритма Кули-Тьюки составляет [math]O(\epsilon \log N)[/math] (для сравнения - относительная ошибка преобразования Фурье непосредственно по формуле дискретного преобразования Фурье - [math]O(\epsilon N^{3/2})[/math]) ^[2]. Поэтому для ускорения алгоритма можно использовать одинарную точность представления переменных без существенного увеличения ошибки.

2.2 Локальность данных и вычислений

В настоящем разделе мы рассмотрим свойства приведенного выше последовательного алгортитма с точки зрения оптимальности взаимодействия с кэш-памятью. С этой точки зрения ключевым фактором является локальность обращений к этой памяти - как пространственная локальность (обращение к близко раположенным адресам), так и временная (частое обращение к одним и тем же адресам). В случае, если алгоритм не обладает достаточной локальностью обращений к памяти, будут происходить частые обращения к более медленной памяти (кэш-памяти более высокого уровня или основной оперативной памяти) - т.н. кэш-промахи. Один кэш-промах на уровне L1 на современных процессорах "стоит" около 10 циклов, а на более высоких уровнях кэша - до 200 циклов.

Ниже мы приводим статистику по кэш-промахам обсуждаемого алгоритма, собранную утилитой cachegrind , входящей в состав пакета valgrind. Расчет произведены на процессоре Intel® Core™ i7-3520M CPU @ 2.90GHz × 4 со следующими уровнями кэш-памяти: L1d 32 КБ, L1i 32 КБ, L2 256 КБ, L3 4096 KБ (буквы i, d означают кэш для инструкций и кэш для данных, соответственно). В расчетах использовалась двойная точность.

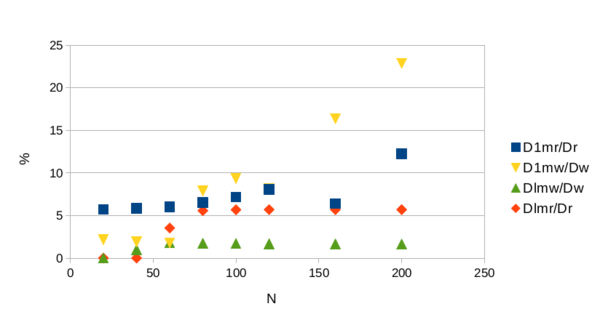
Доля кэш-промахов при реализации алгоритма на трехмерных сетках размера [math]N\times N\times N[/math]. Dw - общее число операций записи, Dr - общее число операций чтения, D1mr - промах чтения из кэш 1-го уровня, D1mw - промах записи в кэш 1-го уровня, Dlmr - промах чтения из кэш верхнего (в данном случае, 3-го) уровня, Dlmw - промах записи в кэш верхнего уровня

Из приведенной картинки можно сделать несколько выводов. Во-первых, количество промахов в кэш первого уровня больше, чем в кэш 3-го уровня, и это связано с соотношением размеров этих уровней. Во-вторых, с увеличением размера задачи кэш-промахи учащаются. В связи с этим отметим, что в тестируемом коде используется несколько трехмерных массивов, размер которых даже в задаче [math]20\times 20 \times 20[/math] не умещается в кэш 1-го уровня. Поэтому относительно небольшая доля кэш-промахов 1-го уровня свидетельствует об работе аппаратного алгоритма предварительной загрузки (предвыборки) в кэш (prefetching). Однако, при росте размера массивов, этот алгоритм, по-видимому, становится менее эффективным.

2.3 Возможные способы и особенности параллельной реализации алгоритма

Как было показано выше, существует, по меньшей мере, два уровня параллелизма в описываемом алгоритме. Во-первых, это параллельная реализация одномерных БПФ и, во-вторых, координатный параллелизм -- параллельное исполнение независимых одномерных БПФ. Эти два уровня могут быть скомбинированы, например, путем распределения разных БПФ между MPI-процессами, а каждого отдельного БПФ - между нитями на общей памяти (POSIX, OpenMP, и т.д.).

Рассмотрим соотношение вычислений и пересылок данных при MPI-реализации. Как показано выше, вычислительная сложность алгоритма при покоординатном распараллеливании, при запуске на [math]N^2[/math] MPI-процессах составляет [math] 6N(\log_2 N) + N[/math], или [math] \left(6N^3(\log_2 N) + N^3\right)/M[/math], на [math]M[/math] процессах.

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

↑ Марчук Г.И. Методы вычислительной математики, М., 1977, 456с.
↑ Gentleman, W. M.; Sande, G. (1966). "Fast Fourier transforms—for fun and profit". Proc. AFIPS 29: 563–578. doi:10.1145/1464291.1464352

Основные авторы описания: В.М.Степаненко, Е.В.Мортиков

4 Свойства и структура алгоритма

4.1 Общее описание алгоритма