Участник:Илья Карандеев(ВТМ, 403)/QR-Факторизация методом Хаусхолдера

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Ниже приведена моя реализация QR-факторизации методом Хаусхолдера. Это для одного процесса, нераспараллеленная программа. Ее ядро (то что отнимает больше всего времени при счете) - функции из cblas на 52-58 строке. После факторизации производится проверка - подсчет погрешности отношения нормы разности произведения вычисленных Q и R матриц и изначальной A-матрицы к норме матрицы A. Вычисленный порядок погрешности на персональном компьютере примерно 10^(-14), что есть довольно хорошо.

2.4 Масштабируемость алгоритма и его реализации

Вот исследование масштабируемости параллельной реализации QR-факторизации квадртной матрицы методом Хаусхолдера. Оно проводилось на суперкомпьютере "Ломоносов-2" суперкомпьютерного комплекса МГУ. В первом эксперименте, эксперименте на сильную масштабируемость, бралась матрица размером 14000 на 14000. Количество процессов в эксперименте рассматривалось таким: 1, 2, 4, 8. 14, 28, 56, 112, 224, 448, 700. Этот выбор обусловлен тем, что в одном узле на суперкомпьютере "Ломоносов-2" 14 ядер, а доступное количество узлов автору было равным 50. То есть максимум можно было задействовать 700 ядер.

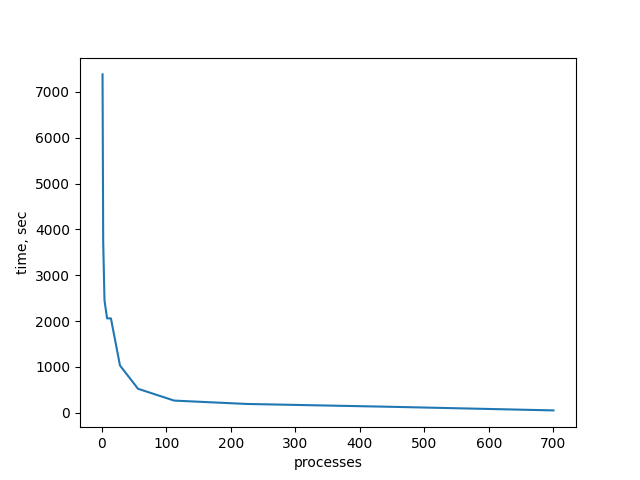
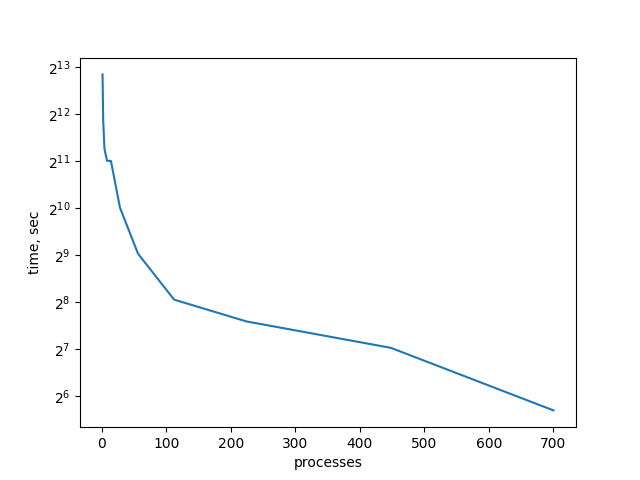
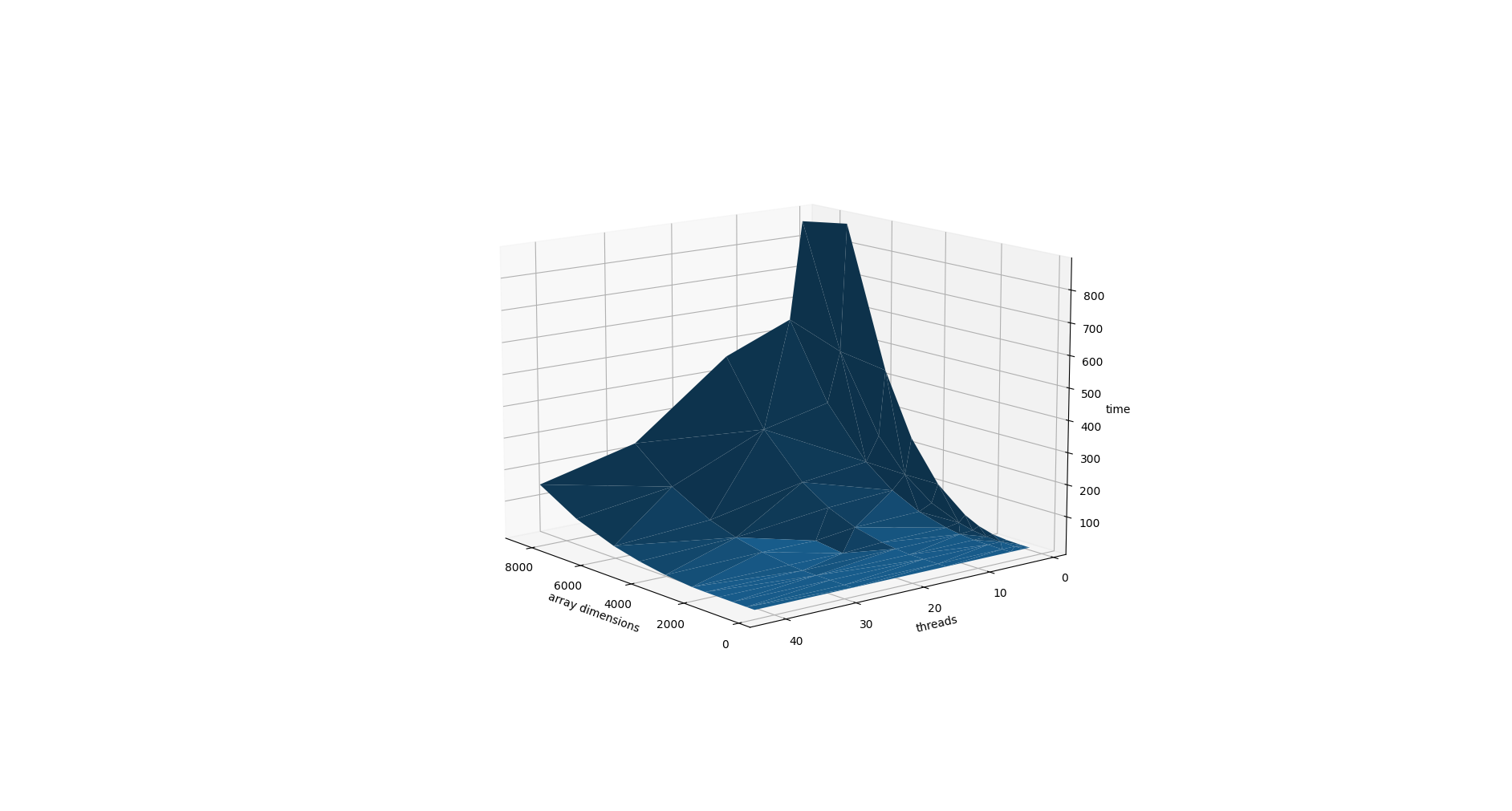
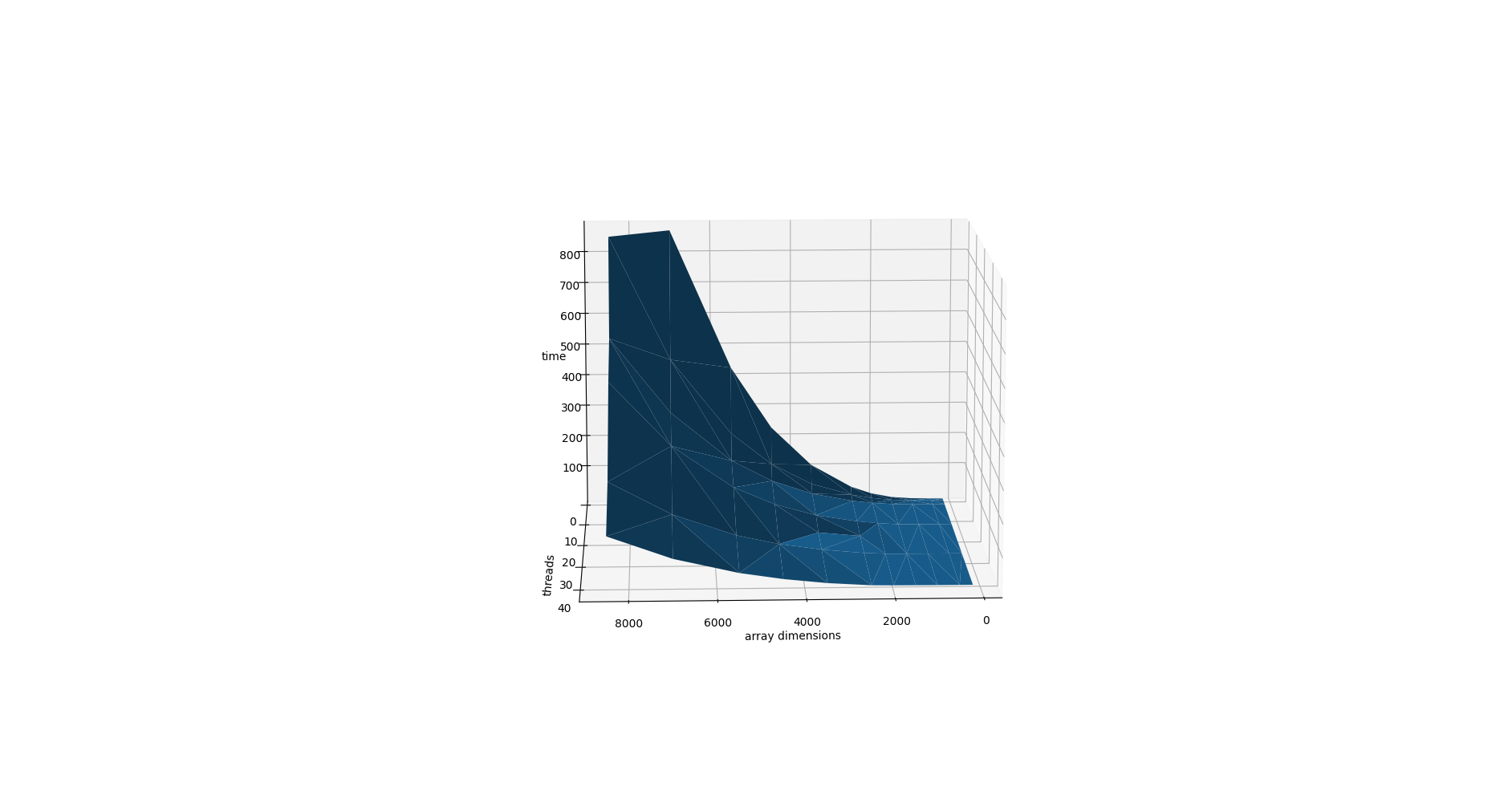
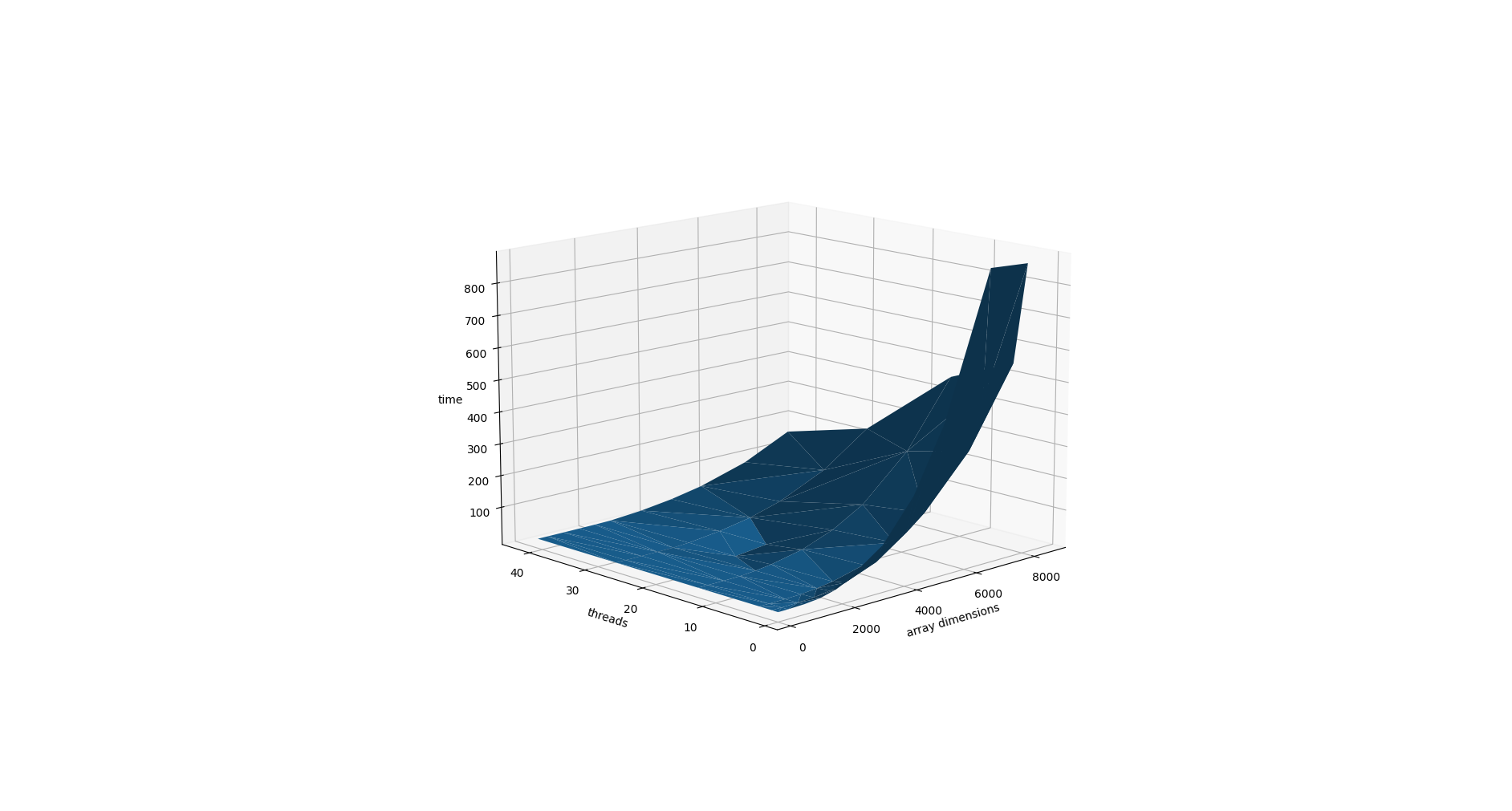
Следующая серия экспериментов на масштабируемость была проведена на 1, 2, 4, 14, 28 и 42 ядрах. Для матриц от 200 до 8500, выбранных более-менее произвольно. Вот график в разных проекциях, полученный по результатам экспериментов.

В целом, все работает объяснимо: больше размерность матрицы → больше время счета. Больше процессов → меньше время счета. Можно заметить, что на малых размерах матрицы при большом количестве процессов начинает падать эффективность. Возможно, это из-за накладных расходов из-за обмена сообщениями между процессами.

2.7 Существующие реализации алгоритма

Большинство пакетов: LINPACK, LAPACK, SCALAPACK и прочие - используют для QR-разложения матриц именно метод Хаусхолдера, правда, в различных модификациях (обычно с использованием BLAS). Существует большая подборка исследовательских работ по блочным версиям.

Можно найти и много пользовательских реализаций:

На языке Python: https://www.quantstart.com/articles/QR-Decomposition-with-Python-and-NumPy/
https://gist.github.com/Hsankesara/cd35edb30825df19f182a6ecf96e126e

На языке R: https://rpubs.com/aaronsc32/qr-decomposition-householder - R

Для MatLab: https://www.mathworks.com/matlabcentral/answers/169648-qr-factorization-using-householder-transformations

3 Литература

В. Б. Андреев: "Численные методы"