Cooley-Tukey, locality
Основные авторы описания: И.В.Афанасьев
Содержание
1 Программная реализация алгоритма: Cooley-Tukey, locality
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel). Условия запуска описаны здесь.
1.1 Локальность данных и вычислений
1.1.1 Локальность реализации алгоритма
1.1.1.1 Структура обращений в память и качественная оценка локальности
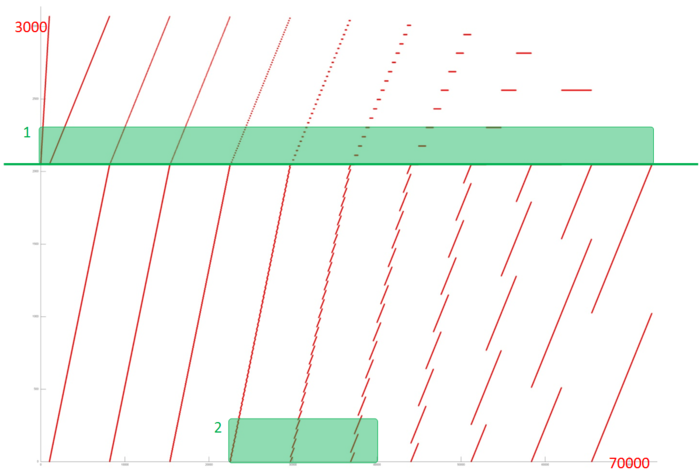
На рис. 1 представлен профиль обращений в память для реализации простого алгоритма Кули-Тьюки быстрого преобразования Фурье для степеней двойки. Данный профиль состоит из обращений к двум массивам (разделены зеленой линией). В целом можно увидеть, что общее число обращений заметно больше числа задействованных данных, поэтому многие элементы используются повторно. Также видно, что вначале элементы обоих массивов перебираются последовательно, однако затем порядок обращений изменяется. Чтобы понять, как устроено это изменение, рассмотрим профиль подробнее.
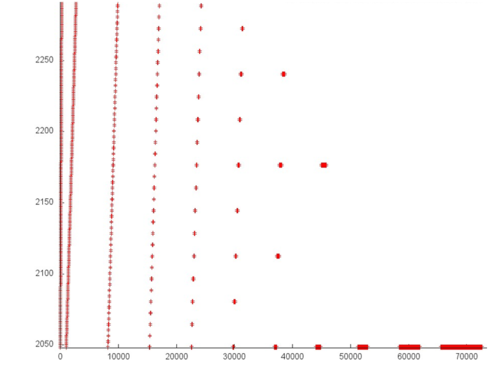
На рис. 2 представлен фрагмент 1 – обращения к началу первого массива на протяжении всей программы. Видно, что при каждом следующем переборе массива задействуется все меньше элементов – возрастает шаг, с которым выбираются элементы. Такое поведение характеризуется средней локальностью – с каждой итерацией увеличивается шаг, а значит, и ухудшается пространственная локальность. Однако при этом число обращений на итерацию уменьшается, а значит, уменьшается время до повторного обращения, т.е. улучшается временная локальность.
Особенно стоит отметить конец фрагмента, где видно множество обращений к самому началу массива. Из рис. 1 видно, что есть еще несколько элементов массива, к которым в конце профиля выполняется множество обращений. Такой профиль является идеальным с точки зрения локальности – и пространственная, и временная локальности принимают практически максимальное значение.
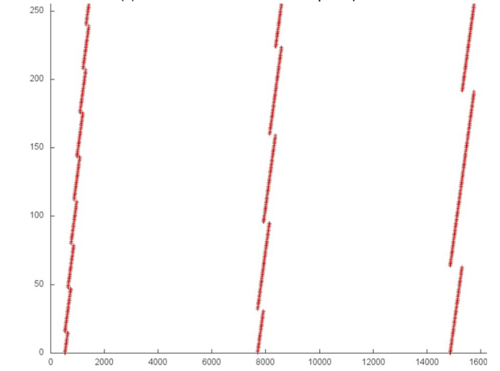
Далее рассмотрим рис. 3, на котором представлен характерный фрагмент для второго массива. Здесь можно увидеть, что строение каждой итерации очень похоже, только при переходе к следующей итерации увеличивается в 2 раза шаг по памяти, в результате чего видимые отрезки на рисунке увеличиваются вдвое. Такой фрагмент обладает не очень высокой пространственной локальностью, что связано с изменением шага, а также не очень высокой временной локальностью, поскольку между повторными обращениями на разных итерациях выполняется достаточно много обращений.
В целом можно сказать, что основная масса обращений общего профиля показывает среднюю локальность, как пространственную, так и временную. Однако отмеченные в конце первого массива обращения к одним и тем же элементам могут в значительной степени повлиять на общую оценку.
1.1.1.2 Количественная оценка локальности
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
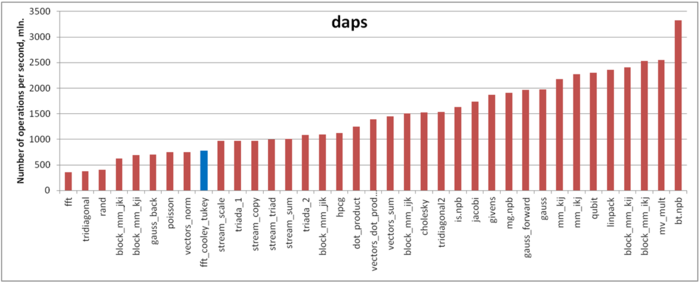
На рисунке 4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что данная программа показывает результат немного хуже среднего, что примерно соответствует нашим ожиданиям согласно качественной оценке. Отметим, что вывод относительно среднего значения делается на основе анализа абсолютных значений, а не положения на графике (здесь не представлена часть программ с низкими значениями). Обратим внимание, что значение daps очень близко к daps для реализации уравнения Пуассона. Это вполне закономерно, поскольку данная реализация построена с использованием данной реализации БПФ.
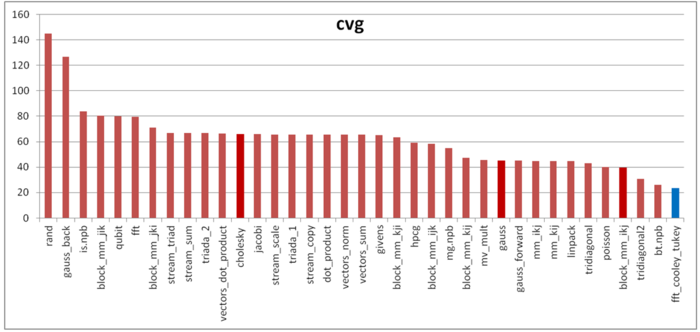
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рисунке 5 значения приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что данная реализация показывает наилучшее значение cvg среди всех рассмотренных программ. Это в определенной степени не соответствует качественному анализу и оценка daps. По всей видимости, здесь повлиял отмеченный выше фрагмент с обращениями к одним и тем же элементам, который в значительной степени улучшил значение оценки. Вероятно, стоит рассмотреть возможность модификации cvg для более аккуратного учета таких случаев.