Cooley-Tukey, scalability

Основные авторы описания: А.М.Теплов (раздел 1.2)

1 Программная реализация алгоритма: Cooley-Tukey, scalability

Исследованная параллельная реализация алгоритма.

1.2 Масштабируемость алгоритма и его реализации

1.2.2 Масштабируемость реализации алгоритма

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [4, 8 : 64] с шагом 8;
• размер вектора [128 : 32768] с шагом равным степени двойки.

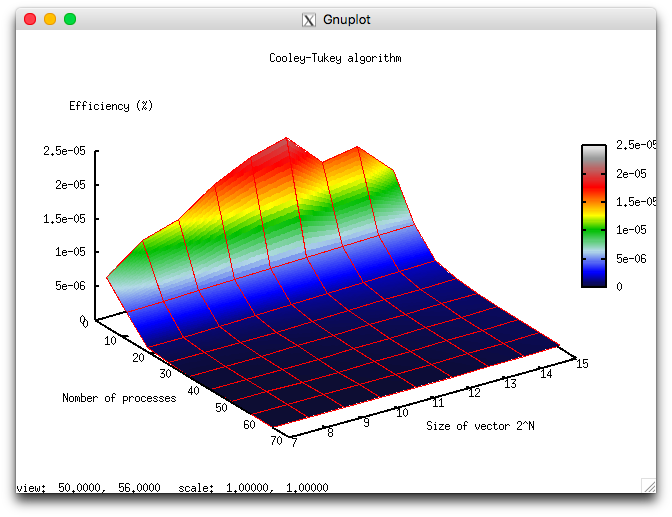
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 0.000000002% (1.85994069951e-09%);
• максимальная эффективность реализации 0.00002% (2.07351573426e-05%).

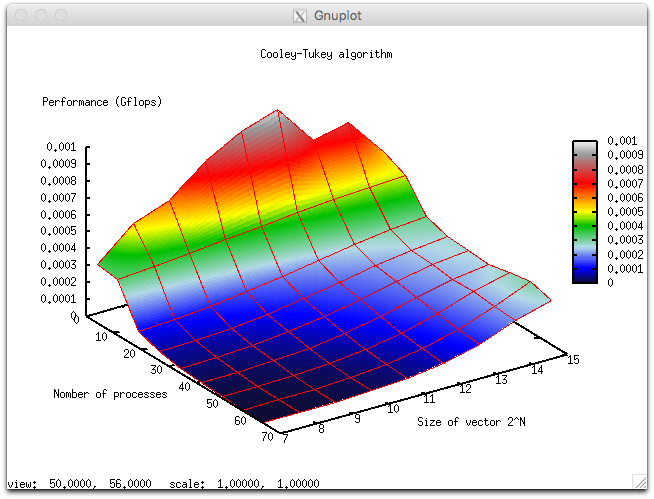
На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.

Рисунок 1. Параллельная реализация алгоритма. Изменение производительности в зависимости от числа процессоров и размера области.

Рисунок 2. Параллельная реализация алгоритма. Изменение эффективности в зависимости от числа процессоров и размера матрицы.

Алгоритм в силу своих особенностей имеет крайне низкую эффективность параллельного выполнения, связанную с крайне малым объемом вычислений на каждый процесс. Из-за этого накладные расходы на организацию параллельного выполнения становятся доминирующими при выполнении алгоритма.