Floyd-Warshall, scalability

Основные авторы описания: Екатерина Шевченко

3 Масштабируемость алгоритма и его реализации

3.1 Масштабируемость алгоритма

Возможность обрабатывать фрагменты независимо означает хорошую масштабируемость алгоритма. Сдерживающие факторы:
1)Пропускная способность памяти при чтении данных графа.
2)Соперничество потоков при выполнении атомарных операций с памятью.
3)Синхронизация после каждого подшага алгоритма.

Алгоритм Флойда-Уоршелла обладает большим потенциалом масштабируемости, так как вычисление кратчайших путей можно распределить между независимыми процессами вплоть до вычисления каждым отдельным процессом одного элемента матрицы смежности.

3.2 Масштабируемость реализации алгоритма

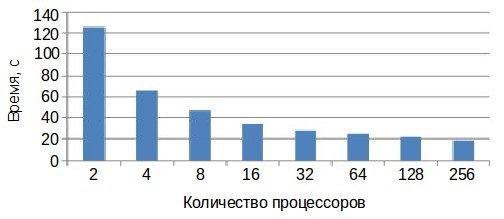
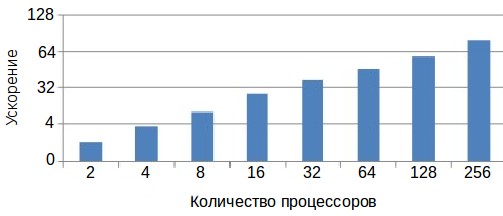
Проведём исследование масштабируемости параллельной реализации алгоритма. Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова. Сильная масштабируемость показывает, как меняется время решения задачи с увеличением количества процессоров (или вычислительных узлов) при неизменном общем объёме задачи.

Сравнение времени параллельной работы алгоритма Флойда-Уоршелла в зависимости от количества процессоров.

Ускорение параллельного алгоритма Флойда-Уоршелла с ростом числа процессоров.

Как видно из представленных графиков параллельный алгоритм сильно масштабируем.