Lanczos, C++, MPI

1 Ссылки

Для исследования масштабируемости рассматриваемого алгоритма Ланцоша без переортогонализации была реализована [программа на языке С++ с использованием технологии MPI https://sebsauvage.net/paste/?b5a95d1025186a6a#JtyXiy7JjDZHAHzZNPhuZp8bCwwYJ7DxzntaYS1KGO0=].

3 Масштабируемость алгоритма и его реализации

3.2 Масштабируемость реализации алгоритма

Дальнейшее исследование было проведено на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса МГУ.

Важно отметить, что реализованная программа выполняет только первую часть алгоритма - формирование трёхдиагональной матрицы [math]T_j[/math]. Вторая часть алгоритма (задача поиска собственных значений матрицы [math]T_j[/math]) может быть решена несколькими методами, каждый из которых обладает своей эффективностью распараллеливания и характерными свойствами. Подробно этот вопрос уже обсуждался в статье ранее, поэтому не будем ещё раз заострять на этом внимание и останавливаться.

Сборка осуществлялась со следующими параметрами:

• Компилятор intel/15.0.090
• Openmpi/1.8.4-icc

В серии проведённых расчётов рассматривались следующие числовые значения параметров:

• Размер [math]n[/math] задачи и, соответственно, матрицы [math]A[/math], задействованной в операции умножения на вектор: [2000 : 30000] с шагом 1000
• Число [math]p[/math] процессоров: 1, 2, 4, 16, 32, 48, 64, 96, 128, 192, 256
• Число итераций в алгоритме: [math]k=350[/math]

Число [math]k[/math] взято таким вопреки информации в начале статьи, где говорится, что значение [math]k[/math] редко превышает [math]10^2[/math] (хоть мы и имеем право брать его любым по нашему усмотрению). Это сделано исключительно для лучшей визуализации пиков на графиках в данном разделе и наглядности получаемых результатов, так как при меньших на порядок значениях параметра [math]k[/math] времена выполнения программ были слишком малы даже при минимальных числах процессоров и максимальных размерах [math]n[/math] задачи.
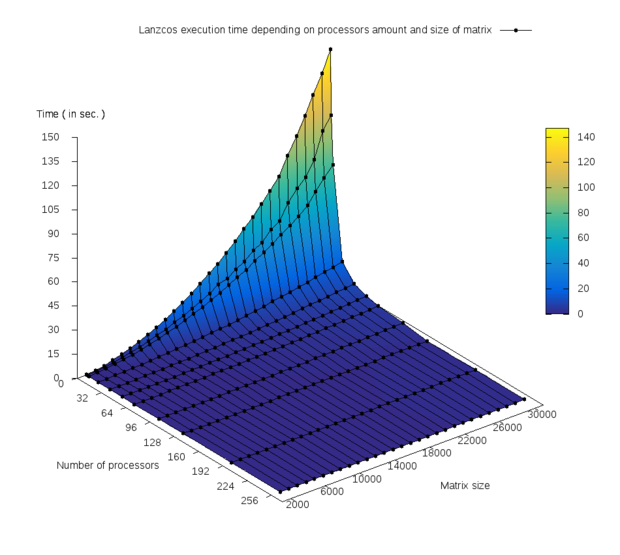
На рис. 1 изображён график зависимости времени выполнения программы от числа процессоров и размера [math]n[/math] задачи.

Рис. 1 График зависимости времени выполнения программы.

Рис. 2 График зависимости эффективности распараллеливания программы.

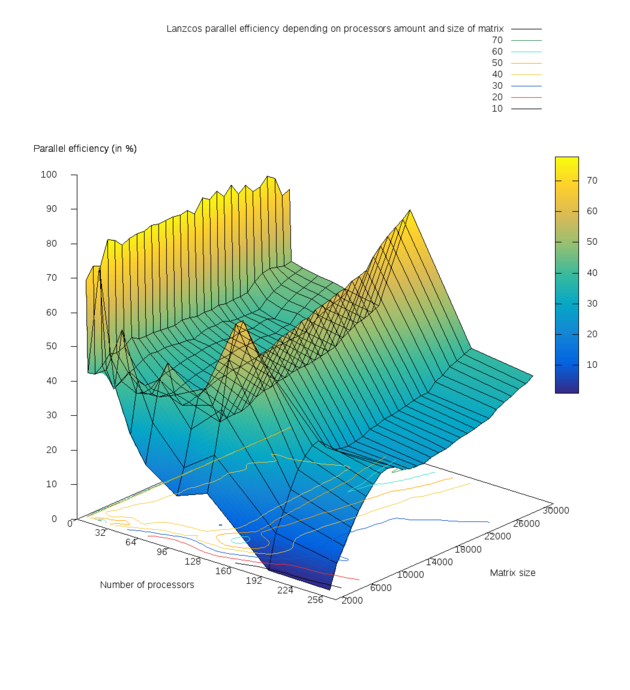
Многочисленные тесты показали при малых количествах ядер уменьшение времени выполнения программы почти в 2 раза при увеличении числа ядер в 2 раза на всём диапазоне размеров матриц, что и отражает сильный излом на первом графике. Изменение значений времени можно легко оценить по предоставленной цветовой шкале. Был построен график эффективности распараллеливания (parallel efficiency) в зависимости от числа процессоров и размера задачи, изображённый на рис. 2. Получены следующие результаты численных экспериментов:

• Средняя эффективность распараллеливания программы составила: 42.5576% ;
• Минимальная эффективность реализации: 0.674% (число процессоров 256 и минимальный размер матрицы 2000);
• Максимальная эффективность реализации: 77.773% (число процессоров 2, размер матрицы 20000).

Нужно понимать, что это лишь экстремумы, соответствующие двум экспериментам, которые сами по себе не дают полной картины и не позволяют однозначно судить о параллельных качествах алгоритма и реализующей его программы при столь большом числе параметров и проводимых расчётов.
На основании рис. 2 можно отметить следующие значимые и важные факты:

• Имеется ярко выраженный спад эффективности при минимальном рассматриваемом размере матрицы [math]n=2000[/math] вдоль всей оси OY, отвечающей за число процессоров;
• Присутствуют два пика эффективности (жёлтого цвета на рис. 3): при числе [math]p[/math] процессоров 2 и 128. Затем при дальнейшем увеличении числа процессоров с 128 до 256 наблюдается постепенное уменьшение эффективности реализации. Это связано с увеличением накладных расходов и затрат времени на обмены сообщениями между процессами.