Dense matrix-vector multiplication, locality
Основные авторы описания: Вад.В.Воеводин (раздел 2)
Содержание
1 Ссылки
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel).
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
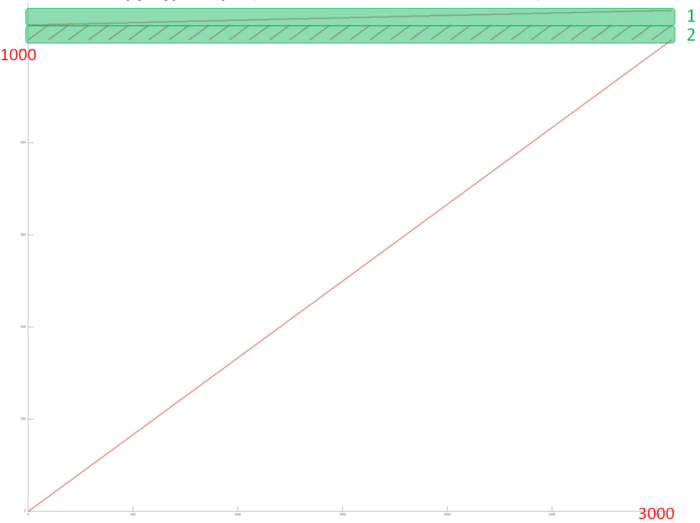
На рис.1 представлен профиль обращений в память для реализации умножения плотной матрицы на вектор. В данном алгоритме задействовано три массива. Выделенный зеленым фрагмент 1 образован обращениями к результирующему вектору; фрагмент 2 – обращениями к исходному вектору; остальные обращения (фрагмент 3) выполняются к матрице, на которую умножается исходный вектор.
Если посмотреть на исходный код, становится понятным, что каждый фрагмент устроен очень просто:
for(int i = 0; i < size; i++)
for(int j = 0; j < size; j++)
vec_out[i] += matrix[i][j] * vec_in[j];
Видно, что фрагмент 1 (обращения к массиву vec_out) состоит из последовательного перебора всех элементов вектора, только к каждому элементу происходит подряд size обращений. Во фрагменте 2 (массив vec_in) выполняется обычный последовательный перебор, который затем повторяется size раз. Фрагмент 3 также представляет собой последовательный перебор всех элементов матрицы, который выполняется только один раз.
Самой высокой локальностью обладает фрагмент 1 из-за повторяющихся подряд обращений к одним и тем же элементам. Однако фрагмент 2 также обладает высокой как пространственной, так и временной локальностью, поскольку число повторных проходов достаточно велико. Фрагмент 3, как и остальные, характеризуется высокой пространственной локальностью (из-за последовательного перебора), однако очень низкой временной локальностью – повторные обращения в нем просто отсутствуют.
2.1.2 Количественная оценка локальности
Условия запуска описаны здесь.
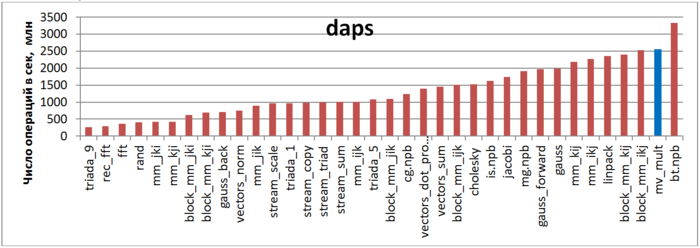
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рис.2 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность данной программы очень высока, даже немного выше, чем производительность теста Linpack. Одна из основных причин этому – очень высокая локальность обращений к векторам.
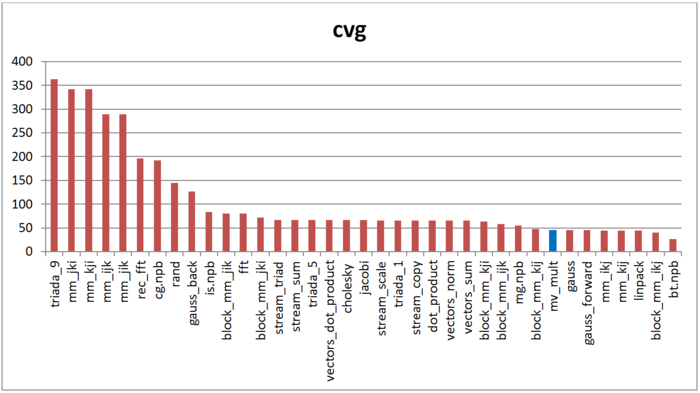
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рис.3 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, локальность реализации умножения матрицы на вектор высока, хотя и не среди первых значений. Однако можно заметить, что полученное значение лишь совсем немного ниже оценки cvg для, например, реализации метода Гаусса или лучших вариантов перемножения матрицы.