HPCG, locality
Основные авторы описания: Вад.В.Воеводин (раздел 2).
Содержание
1 Ссылки
Реализация, на основе которой были получены количественные оценки, приведена здесь (данная реализация взята отсюда).
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
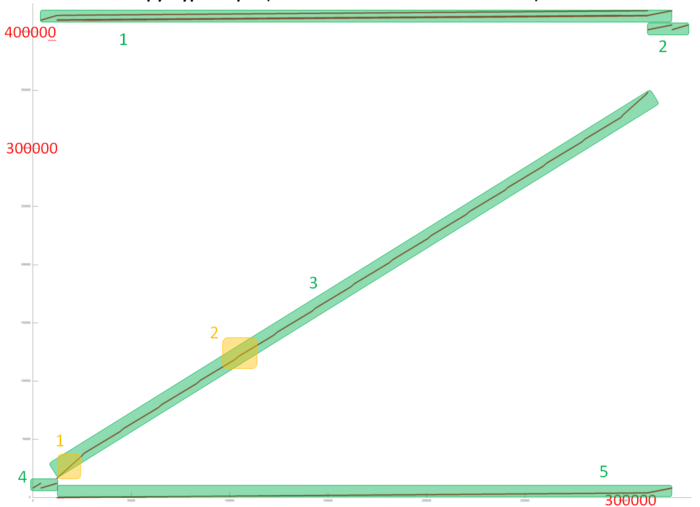
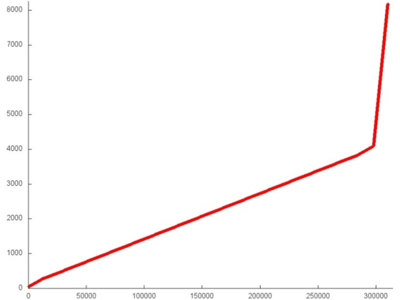
На рис.1 представлен общий профиль обращений в память для теста HPCG. В данном тесте выполняются операции над разреженной матрицей, поэтому большая часть элементов массивов не задействуются (поскольку являются нулевыми). В результате объем задействованной памяти (около 350-400 тысяч обращений) меньше общего числа обращений, т.е. в среднем к каждому элементу было выполнено менее 1 обращения. Данный профиль можно разбить на несколько фрагментов, которые выделены на рис.1 зеленым цветом.
Сразу отметим, что, поскольку в данной программе задействовано очень большое число массивов, мы не можем получать отдельные профили для каждого фрагмента и визуализировать их независимо. Поэтому мы используем фильтрацию общего профиля для получения нужного подмножества обращений. В этом случае графики для фрагментов остаются такими же, как и при независимо построении. Также номер обращения всегда начинается с нуля. Однако значения по оси ординат остаются соответствующими общему профилю и потому начинаются не с нуля.
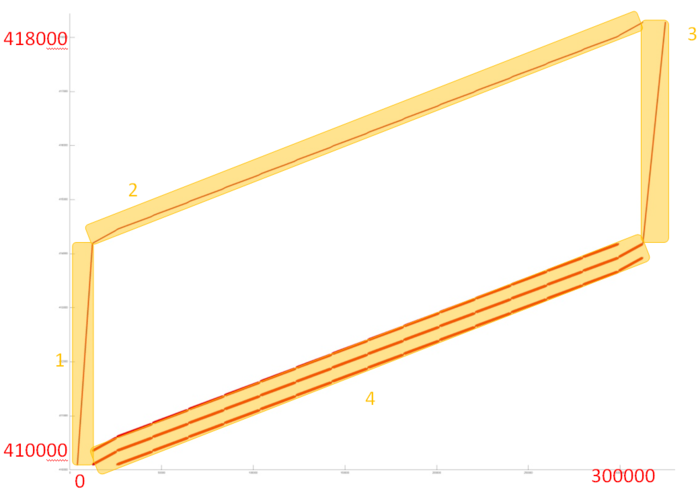
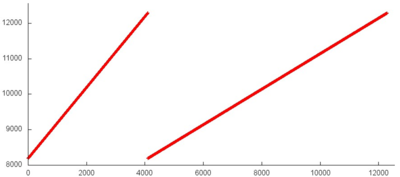
Фрагмент 1 представлен на рис.2. Он устроен достаточно сложно, однако явно обладает регулярной структурой. Для ее понимания рассмотрим отдельно ее различные части, выделенные на рисунке оранжевым цветом.
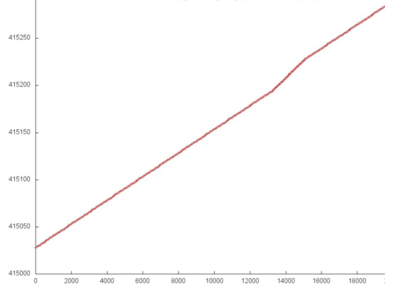
При ближайшем рассмотрении можно увидеть, что часть 1, как и подобная ей часть 3, представляют собой обычный последовательный перебор элементов, возможно, с некоторым небольшим шагом по памяти. На рис.3 представлена область из середины части 2. Можно заметить, что в данном случае также выполняется последовательный перебор элементов, однако шаг по памяти нерегулярный. По всей видимости, это связано с нерегулярностью наполненности разреженной матрицы.
В данном случае нерегулярность перебора элементов не влияет на локальность. Поэтому можно сказать, что части 1-3 обладают высокой пространственной локальностью, поскольку используется шаг по памяти, однако очень низкой временной локальностью, поскольку повторные обращения просто отсутствуют.
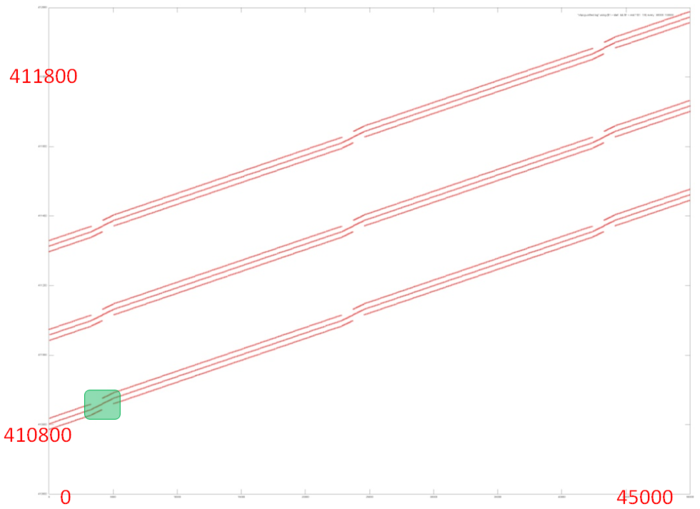
На рис.4 представлена область из середины части 4. При таком приближении заметно, что часть 4 состоит из трех параллельно идущих профилей, каждый из которых состоит из набора подобных итераций, выполняемых над другим набором элементов. Каждый итерация, в свою очередь, состоит из трех параллельно идущих переборов с одинаковым шагом (поскольку наклон линий одинаков).
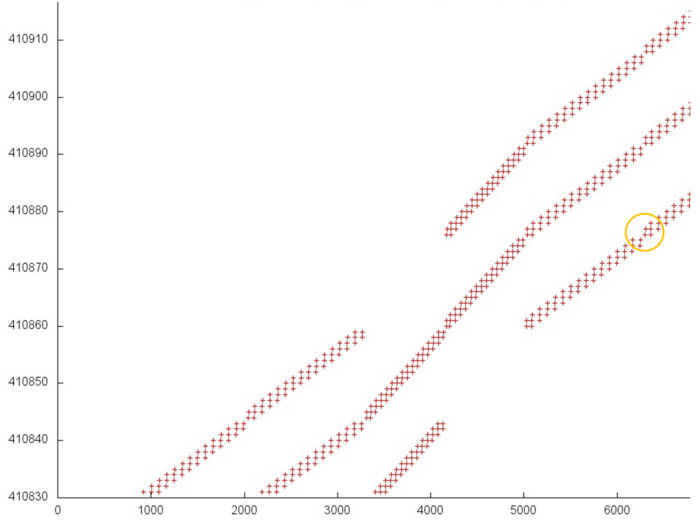
Рассмотрим более подробно область около перехода от одной итерации к другой (рис.5). Видно, что каждая итерация устроена заметно сложнее, чем просто последовательный перебор, однако регулярность обращений подтверждается. Каждый из трех параллельно идущих переборов итерации состоит из набора фрагментов с одинаковой структурой; переход от одного от одного фрагмента к следующему выделен на рисунке оранжевым кругом. Каждый такой небольшой фрагмент представляет собой последовательный перебор с шагом 1, однако на каждом шаге перебора происходит 3 обращения к идущим подряд элементам.
Переход от одной итерации к другой устроен похожим образом, только меняется число параллельно выполняемых переборов.
В целом видно, что часть 4 характеризуется высокой пространственной локальностью – обращения в каждой части выполняются к соседним элементам. При этом временная локальность также высока, поскольку повторные обращения происходят достаточно часто.
В результате про фрагмент 1 можно сказать, что он обладает хорошей пространственной локальностью, поскольку во все частях основным является последовательный перебор или его более сложный аналог. Про временную локальность сделать выводы сложнее, однако, с достаточно большой вероятностью, она тоже достаточно высока, поскольку основная часть обращений сосредоточена в части 4.
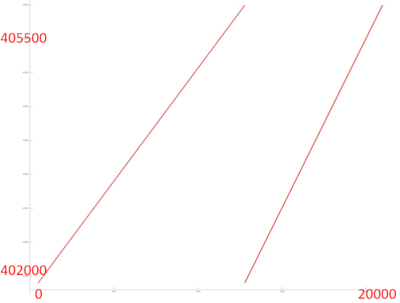
Теперь перейдем к рассмотрению фрагмента 2, профиль обращений которого показан на рис.6. Видно, что данный фрагмент состоит из существенно меньшего числа обращений, чем предыдущий фрагмент, и состоит из двух этапов, каждый из которых похож на перебор элементов массива. Более подробный анализ показывает, что в обоих случаях действительно выполняется обычный простой последовательный перебор с фиксированным шагом. Более того, шаг по памяти у них одинаков, а разный наклон вызван тем, что параллельно с первым перебором выполняется больше обращений к другим массивам, в результате чего кажется, что данный перебор выполняется дольше.
Подобный фрагмент обладает высокой пространственной и низкой временной локальностью.
Фрагмент 3, который задействует наибольший диапазон данных в программе, напоминает перебор элементов с нерегулярным шагом, о чем говорит ломаный характер линии. Отметим, что из рис.1 нельзя понять, не обладает ли на самом деле эта линия более сложным строением. Однако можно предположить, что основная часть фрагмента обладает схожей структурой, а в начале и конце данного фрагмента находятся две похожие области, которые явно отличаются от остальной части. Поэтому рассмотрим отдельно две части, отмеченные на рис.1 оранжевым цветом.
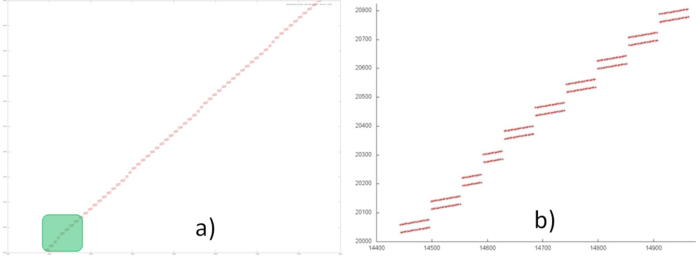
При более близком рассмотрении части 1 (рис.7a) становится понятным, что фрагмент 3 обладает более сложной структурой, чем простой перебор с нерегулярным шагом. Можно заметить наличие подобных областей, которые имеют разный размер, однако по виду схожую структуру. Если выполнить дальнейшее приближение (рис.7b, приближение выделенного зеленым участка на рис.7a), мы увидим, что, действительно, данные небольшие области подобны и представляют собой два параллельно выполняемых перебора элементов.
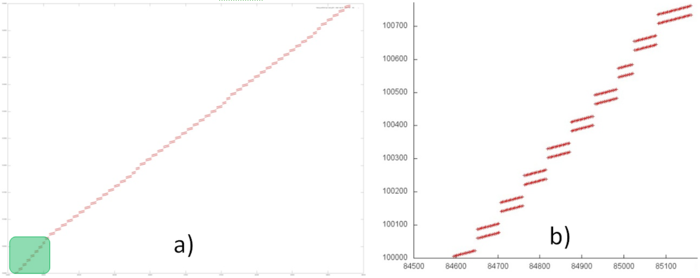
Подробное рассмотрение показывает, что часть 2 фрагмента 3 очень похожей структурой (рис.8). Более того, шаг по памяти примерно одинаков, поэтому можно предположить, что две данные части на самом деле однотипны. В этом случае разница в их представлении на рис.1 вызвана разным числом обращений к другим массивам: одновременно с частью 1 выполнялось меньше обращений к другим массивам, поэтому на графике угол наклона этой части кажется больше.
Таким образом, можно сказать, что данный фрагмент обладает достаточно высокой пространственной локальностью, поскольку зачастую следующее обращение происходит к соседнему элементу, и не очень высокой временной локальностью, поскольку число повторных обращений достаточно мало, хотя они и расположены близко друг к другу.
Фрагмент 4, представленный на рис.9, обладает ровно такой же структурой, что и фрагмент 2; меняется только число обращений, и как следствие, вероятно, число задействованных элементов.
Перейдем к рассмотрению последнего фрагмента. На рис.10 явно выделяется две области, однако в данном случае, также как и в остальных фрагментах, изменение в угле наклона связано с параллельно выполняемыми обращениями к другим массивам, и на самом деле структура двух областей одинакова.
При дальнейшем рассмотрении становится понятным, что данный профиль на самом деле представляет собой обычный последовательный перебор элементов с шагом 1.
В целом общий профиль рассматриваемой программы обладает непростой и не всегда регулярной структурой, поэтому сложно делать предположения относительно локальности в целом. Однако если резюмировать полученные выводы по фрагментам, можно предположить следующее, что пространственная локальность всего профиля достаточно высока, поскольку часто встречаются последовательные переборы; при этом временная локальность, наоборот, достаточно низка, так как повторные обращения встречаются нечасто.
2.1.2 Количественная оценка локальности
Условия запуска описаны здесь.
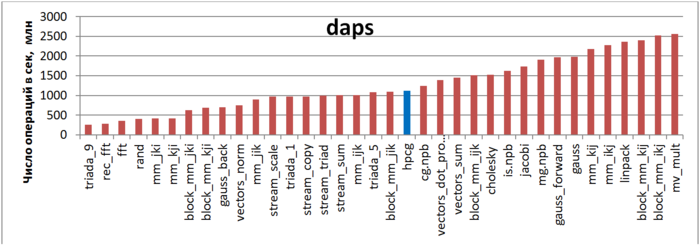
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рис.11 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что, несмотря на работу с разреженной матрицей, данная программа показывает достаточно высокие результаты, значительно выше теста со случайным доступом (rand) или обратного хода метода Гаусса решения СЛАУ (gauss_back).
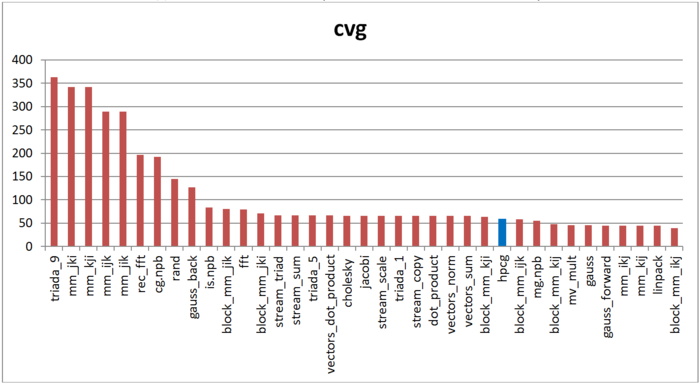
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рис.12 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, результаты hpcg даже несколько лучше по сравнению с оценкой daps. В первую очередь это связано с высокой пространственной локальностью, однако означает, что и временная локальность не так уж низка.