Repeated two-sided Thomas, locality
Содержание
1 Ссылки
2 Локальность данных и вычислений
Как видно по графу алгоритма, локальность данных по пространству хорошая - все аргументы, что нужны операциям, вычисляются "рядом". Однако по времени локальность вычислений не столь хороша. Если данные задачи не помещаются в кэш, то вычисления в "верхнем левом" и "нижнем правом" "углах" СЛАУ будут выполняться с постоянными промахами кэша. Отсюда может следовать одна из рекомендаций прикладникам, использующим прогонку, - нужно организовать все вычисления так, что бы прогонки были "достаточно коротки" для помещения данных в кэш.
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
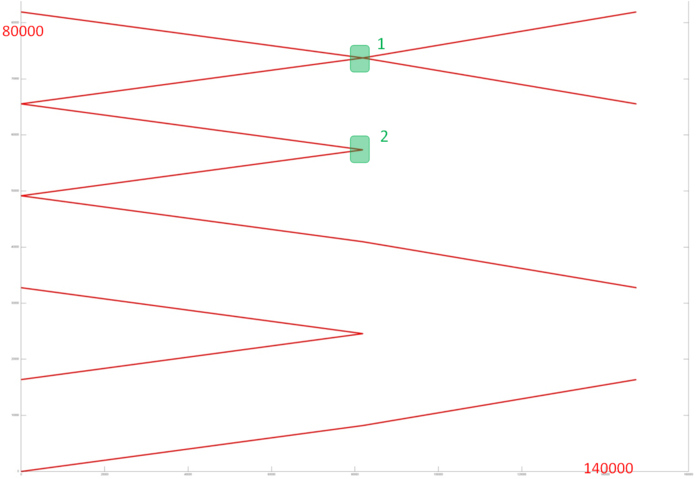
На рис. 1 представлен профиль обращений в память для реализации повторного варианта встречной прогонки. Данный профиль состоит из набора параллельно выполняемых последовательных переборов, как возрастающих, так и убывающих. В общем случае такой профиль характеризуется высокой пространственной локальностью, поскольку соседние обращения выполняются к близким по памяти данным, а также низкой временной локальностью, так как данные практически не используются повторно. Это подтверждает тот факт, что общее число обращений в память менее чем в два раза превышает число задействованных данных – достаточно плохой показатель производительности работы с памятью.
Из рисунка можно предположить, что переборы, скорее всего, устроены достаточно регулярно и не меняют своего поведения в течение программы. Однако нужно детально разобрать, как устроены эти переборы; для этого рассмотрим некоторые наиболее интересные фрагменты профиля более детально.
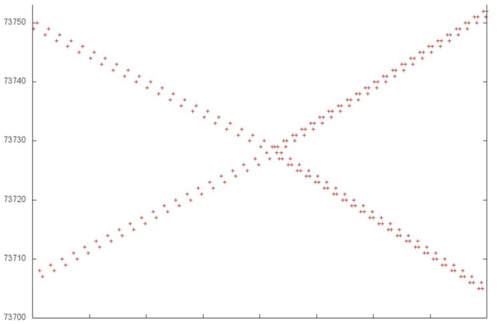
На рис. 2 приведен фрагмент 1 (выделен на рис. 1 зеленым). Видна регулярность обращений к памяти, которая нарушается только один раз, примерно по центру рисунка, где происходит смена этапов работы программы. На первом этапе параллельно выполняются два возрастающих и два убывающих последовательных перебора с небольшим шагом по памяти; на втором этапе число переборов возрастает в 1.5 раза, однако характер обращений остается примерно тем же. Подобный фрагмент, в отличие от обычного последовательного перебора, обладает более высокой временной локальностью, поскольку данные используются повторно по несколько раз, при этом большая часть повторных обращений расположена близко друг к другу.
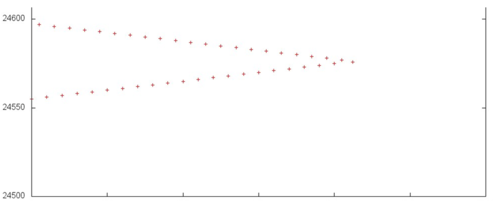
Далее рассмотрим фрагмент 2 (рис. 3). Здесь профиль устроен очень просто – параллельно выполняются возрастающий и убывающий переборы данных с небольшим шагом по памяти. Подобное поведение можно увидеть также во всех переборах, расположенных ниже фрагмента 2 на рис. 1.
В целом можно сказать, что данный профиль действительно состоит из небольшого числа возрастающих и убывающих последовательных переборов с небольшим шагом по памяти. Такое строение характеризуется высокой пространственной и достаточно низкой временной локальностью.
2.1.2 Количественная оценка локальности
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
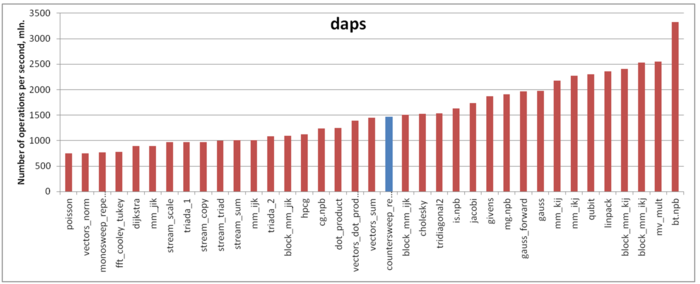
На рисунке 4 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что реализация данного алгоритма показывает достаточно неплохую производительность работы с памятью. Результаты daps примерно совпадают с результатами для реализации метод Холецкого и обгоняют большинство других алгоритмов, построенных на основе переборов элементов массива, таких как вычисление скалярного произведения, реализация повторного варианта монотонной прогонки и т.д.
3 Масштабируемость алгоритма и его реализации
О масштабируемости самой повторной встречной прогонки, как почти непараллельного алгоритма, говорить нельзя в принципе, за исключением разве что двухпроцессорных систем. Понятие масштабируемости неприменимо, поскольку описываемый алгоритм не предполагает параллельной реализации.
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
4 Динамические характеристики и эффективность реализации алгоритма
В силу существенно последовательной природы алгоритма и его избыточной локальности, исследование его динамических характеристик представляется малоценным.