Встречная прогонка, блочный вариант
| Встречная прогонка блочно-трёхдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | 8n-2 макроопераций |
| Объём входных данных | 4n-2 блоков |
| Объём выходных данных | n блоков |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | 2.5n-1 макроопераций |
| Ширина ярусно-параллельной формы | 4 макроопераций |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Встречная блочная прогонка - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида Ax = b, где
- A = \begin{bmatrix} A_{11} & A_{12} & 0 & \cdots & \cdots & 0 \\ A_{21} & A_{22} & A_{23}& \cdots & \cdots & 0 \\ 0 & A_{32} & A_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & A_{n-1 n-2} & A_{n-1 n-1} & A_{n-1 n} \\ 0 & \cdots & \cdots & 0 & A_{n n-1} & A_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \\ \end{bmatrix}, b = \begin{bmatrix} B_{1} \\ B_{2} \\ \vdots \\ B_{n} \\ \end{bmatrix}
Часто, однако, при изложении сути метода блочной прогонки[3] блоки правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид (N=n+1)
- A = \begin{bmatrix} C_{0} & -B_{0} & 0 & \cdots & \cdots & 0 \\ -A_{1} & C_{1} & -B_{1} & \cdots & \cdots & 0 \\ 0 & -A_{2} & C_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -A_{N-1} & C_{N-1} & -B_{N-1} \\ 0 & \cdots & \cdots & 0 & -A_{N} & C_{N} \\ \end{bmatrix}\begin{bmatrix} Y_{0} \\ Y_{1} \\ \vdots \\ Y_{N} \\ \end{bmatrix} = \begin{bmatrix} F_{0} \\ F_{1} \\ \vdots \\ F_{N} \\ \end{bmatrix}
Блочная встречная прогонка, как и монотонная, заключается в исключении из уравнений неизвестных, однако, в отличие от монотонной, в ней исключение ведут одновременно с обоих "краёв" СЛАУ (верхнего и нижнего). В принципе, её можно считать самым простейшим вариантом метода редукции (при m=1 и встречных направлениях монотонных блочных прогонок).
1.2 Математическое описание алгоритма
m здесь - номер уравнения, на котором "встречаются" две ветви прямого хода - "сверху" и "снизу".
В приведённых обозначениях во встречной прогонке сначала выполняют её прямой ход - вычисляют коэффициенты
"сверху":
\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0},
\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0},
\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}, \quad i = 1, 2, \cdots , m-1,
\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i}), \quad i = 1, 2, \cdots , m-1,
и "снизу":
\boldsymbol{\xi}_{N} = C_{N}^{-1} A_{N},
\boldsymbol{\eta}_{1} = C_{N}^{-1} F_{N},
\boldsymbol{\xi}_{i} = (C_{i}-B_{i}\boldsymbol{\xi}_{i+1})^{-1} A_{i}, \quad i = N-1, N-2, \cdots , m,
\boldsymbol{\eta}_{i} = (C_{i}-B_{i}\boldsymbol{\xi}_{i+1})^{-1}(F_{i}+B_{i}\boldsymbol{\eta}_{i+1}), \quad i = N-1, N-2, \cdots , m,
после чего вычисляют решение с помощью обратного хода
Y_{m} = (E-\boldsymbol{\xi}_{m}\boldsymbol{\alpha}_{m})^{-1}(\boldsymbol{\eta}_{m}+\boldsymbol{\xi}_{m}\boldsymbol{\beta}_{m}),
Y_{m-1} = (E-\boldsymbol{\alpha}_{m}\boldsymbol{\xi}_{m})^{-1}(\boldsymbol{\beta}_{m}+\boldsymbol{\alpha}_{m}\boldsymbol{\eta}_{m}),
Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}, \quad i = m-1, m-2, \cdots , 1, 0,
Y_{i+1} = \boldsymbol{\xi}_{i+1} Y_{i} + \boldsymbol{\eta}_{i+1}, \quad i = m, m+1, \cdots , N-1.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно, как и в случае блочной монотонной прогонки, представить состоящим из двух частей - прямого и обратного хода; однако их ширина вдвое больше, чем в монотонном случае. В прямом ходе ядро составляют две независимые последовательности умножения обратной к одной матрице на другую, умножения и сложения/вычитания матриц и векторов. В обратном ходе в ядре остаются только две независимые последовательности умножений и сложений матриц и векторов.
1.4 Макроструктура алгоритма
В дополнение к возможности представления макроструктуры алгоритма как совокупности прямого и обратного хода, прямой ход также может быть разложен на две макроединицы - прямой ход правой и левой прогонок, выполняемых "одновременно", т.е., параллельно друг другу, для разных половин СЛАУ. Обратный ход также может быть разложен на две макроединицы - обратный ход правой и левой прогонок, выполняемых "одновременно", т.е., параллельно друг другу, для разных половин СЛАУ. В этом блочная версия встречной прогонки аналогична точечной, с тем различием, что здесь основные операции более "тяжёлые", так как выполняются не над числами, а над блоками.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Инициализируется прямой ход прогонки:
\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0},
\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0},
\boldsymbol{\xi}_{N} = C_{N}^{-1} A_{N},
\boldsymbol{\eta}_{1} = C_{N}^{-1} F_{N}.
2. Последовательно выполняются формулы прямого хода:
\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}, \quad i = 1, 2, \cdots , m-1,
\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i}), \quad i = 1, 2, \cdots , m-1,
\boldsymbol{\xi}_{i} = (C_{i}-B_{i}\boldsymbol{\xi}_{i+1})^{-1} A_{i}, \quad i = N-1, N-2, \cdots , m,
\boldsymbol{\eta}_{i} = (C_{i}-B_{i}\boldsymbol{\xi}_{i+1})^{-1}(F_{i}+B_{i}\boldsymbol{\eta}_{i+1}), \quad i = N-1, N-2, \cdots , m.
3. Инициализируется обратный ход:
Y_{m} = (E-\boldsymbol{\xi}_{m}\boldsymbol{\alpha}_{m})^{-1}(\boldsymbol{\eta}_{m}+\boldsymbol{\xi}_{m}\boldsymbol{\beta}_{m})
Y_{m-1} = (E-\boldsymbol{\alpha}_{m}\boldsymbol{\xi}_{m})^{-1}(\boldsymbol{\beta}_{m}+\boldsymbol{\alpha}_{m}\boldsymbol{\eta}_{m})
4. Последовательно выполняются формулы обратного хода:
Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}, \quad i = m-1, m-2, \cdots , 1, 0,
Y_{i+1} = \boldsymbol{\xi}_{i+1} Y_{i} + \boldsymbol{\eta}_{i+1}, \quad i = m, m+1, \cdots , N-1.
1.6 Последовательная сложность алгоритма
Для выполнения блочной встречной прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется:
- 2n+2 умножений обратного одному блока на другой,
- 3n-2 сложений/вычитаний блоков,
- 3n-2 умножений блоков.
При классификации по последовательной сложности, таким образом, блочная встречная прогонка относится к алгоритмам с линейной макросложностью.
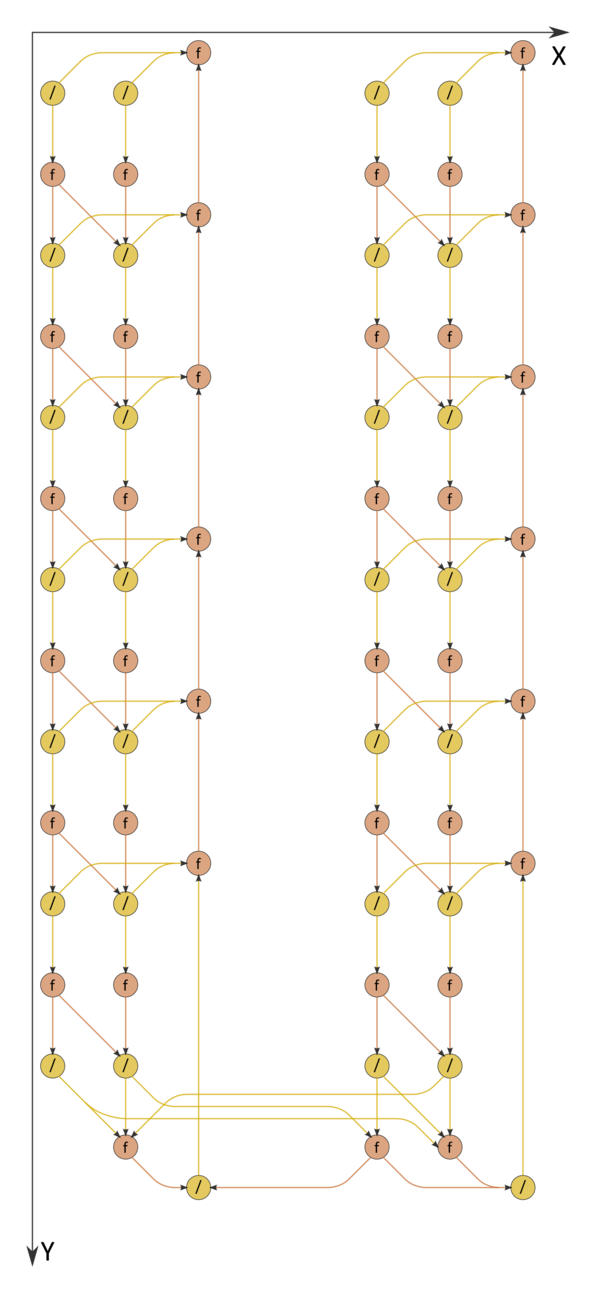
1.7 Информационный граф
Информационный макрограф встречной блочной прогонки изображён на рис.1. Как видно, он параллелен на прямом ходе со степенью не более 4, на обратном - не более 2. При выполнении прямого хода не только ветви, но и две подветви каждой из ветвей (левая - разложение матрицы, правая - решение первой из двухдиагональных систем) могут выполняться параллельно друг другу. Правые подветви соответствуют обратному ходу. По рисунку видно, что не только математическая суть обработки подвекторов, но даже структура графа алгоритма и направление потоков данных в нём вполне соответствуют названию "обратный ход".
1.8 Описание ресурса параллелизма алгоритма
Обе ветви прямого хода выполняются одновременно для N=2m-1, т.е. для n=2m. Тогда для выполнения встречной блочной прогонки требуется последовательно выполнить следующие ярусы:
- m+1 ярусов умножения блока, обратного к одному, на другой или на вектор (в каждом из ярусов, кроме одного, по 4 таких операции, в одном - 2),
- по 2m-1 ярусов умножений и сложений/вычитаний блоков (в m-1 ярусах - по 4 операции, в m-1 - по две, в одном - три операции).
При классификации по высоте ЯПФ, таким образом, блочная встречная прогонка относится к алгоритмам со сложностью O(n макропераций. При классификации по ширине ЯПФ его макросложность будет равна 4.
При нечётном n ветви нельзя выполнить синхронно, поэтому предпочтительнее выбирать чётные размеры задач.
1.9 Входные и выходные данные алгоритма
Входные данные: блочно-трёхдиагональная матрица A (блоки A_{ij}), вектор B (блоки B_{i}).
Выходные данные: вектор X (блоки X_i ).
Объём выходных данных: n блоков.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности, как хорошо видно, является константой (зависящей от размера блоков).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – тоже константа.
Алгоритм в рамках выбранной версии полностью детерминирован.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 блочными строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже элементов матрицы либо отдельно).
2.2 Возможные способы и особенности параллельной реализации алгоритма
Встречная прогонка задумана изначально для случая, когда нужно найти только какую-то близкую к "середине" блочную компоненту вектора решения, а остальные были не нужны (решение т.н. "частичной задачи"). При появлении параллельных компьютерных устройств оказалось, что у встречной блочной прогонки есть небольшой дополнительный ресурс параллелизма. Однако для получения массового параллелизма встречная блочная прогонка должна быть распараллелена на уровне блочных операций.