Метод Ньютона для систем нелинейных уравнений

Основные авторы статьи: К.О.Шохин и А.А.Лебедев,
О.Р.Гирняк и Д.А.Васильков (раздел 1.7).

Метод Ньютона решения систем нелинейных уравнений
Последовательный алгоритм
Последовательная сложность	[math]O(L \cdot n^3)[/math], если для решения СЛАУ использовать метод Гаусса, алгоритм сойдется за [math]L[/math] итераций, вычисление значения каждой функции системы и их производных в точке имеет оценку сложности [math]O(n)[/math]
Объём входных данных	[math]n[/math] функций от [math]n[/math] переменных, [math]n^2[/math] частных производных этих функций по каждой переменной, [math]n[/math]-мерный вектор(начальное приближение решения), [math]\varepsilon[/math] - требуемая точность, [math]{\rm max\_iter}[/math] - максимальное число итераций
Объём выходных данных	[math]n[/math]-мерный вектор

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Ньютона решения систем нелинейных уравнений является обобщением метода Ньютона решения нелинейных уравнений, который основан на идее линеаризации. Пусть [math] F(x) : {\mathbb R}^1 \to {\mathbb R}^1[/math] - дифференцируемая функция и необходимо решить уравнение [math]F(x) = 0[/math].

Взяв некоторое [math]x_0[/math] в качестве начального приближения решения, мы можем построить линейную аппроксимацию

[math]F(x)[/math] в окрестности [math]x_0 : F(x_0+h) \approx F(x_0)+F^\prime(x_0)h[/math] и решить получающееся линейное уравнение [math]F(x_0 )+F^\prime (x_0 )h =0[/math].

Таким образом получаем итеративный метод : [math] x_{k+1} = x_k - {F^\prime(x_k)}^{-1}F(x_k), \ k = 0,1,\ldots [/math] .

Данный метод был предложен Ньютоном в 1669 году. Более точно, Ньютон оперировал только с полиномами; в выражении для [math]F(x+h)[/math] он отбрасывал члены более высокого порядка по h , чем линейные. Ученик Ньютона Рафсон в 1690 г. предложил общую форму метода (т. е. не предполагалось что [math]F(x)[/math] обязательно полином и использовалось понятие производной), поэтому часто говорят о методе Ньютона—Рафсона. Дальнейшее развитие исследований связано с именами таких известных математиков, как Фурье, Коши и другие. Например, Фурье доказал в 1818 г., что метод сходится квадратично в окрестности корня, а Коши (1829, 1847) предложил многомерное обобщение метода и использовал метод для доказательства существования решения уравнения.

1.2 Математическое описание алгоритма

Пусть дана система из [math]n[/math] нелинейных уравнений с [math]n[/math] неизвестными.

[math] \left\{\begin{matrix} f_1(x_1, \ldots, x_n) = 0, \\ f_2(x_1, \ldots, x_n) = 0, \\ \vdots \\ f_n(x_1, \ldots, x_n) = 0. \end{matrix}\right. [/math] , где [math]f_i(x_1, \ldots,x_n) : {\mathbb R}^n \to {\mathbb R}, \ i = 1,\ldots,n[/math] - нелинейные функции, определенные и непрерывно дифференцируемые в некоторой области [math]G \subset {\mathbb R}^n[/math].

Запишем ее в векторном виде:

[math]\overline{x} = {(x_1,x_2,\ldots,x_n)}^T, F(x) ={[f_1(x),f_2(x),\ldots,f_n(x)]}^T, F(x)=0[/math]

Требуется найти такой вектор [math]\overline{x^*} = {(x^*_1,x^*_2,\ldots,x^*_n)}^T[/math], который, при подстановке в исходную систему, превращает каждое уравнение в верное числовое равенство.

При таком подходе формула для нахождения решения является естественным обобщением формулы одномерного итеративного метода:

[math]x^{(k+1)} = x^{(k)} - W^{-1}(x^{(k)})\cdot F(x^{(k)}) , k=0,1,2,\ldots[/math], где

[math] W = \begin{pmatrix} \frac{\partial{f_1(x_1)}}{\partial{x_1}} & \cdots & \frac{\partial{f_1(x_n)}}{\partial{x_n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial{f_n(x_1)}}{\partial{x_1}} & \cdots & \frac{\partial{f_n(x_n)}}{\partial{x_n}} \end{pmatrix}[/math] – матрица Якоби.

В рассмотренных предположениях относительно функции [math]F(\cdot)[/math] при выборе начального приближения [math]x^{(0)}[/math] из достаточно малой окрестности решения [math]\overline{x^*}[/math] имеет место сходимость последовательности [math]\{x^{(k)}\}[/math]. При дополнительном предположении [math]F(\cdot) \in C^2[/math] имеет место квадратичная сходимость метода.

В качестве критерия окончания процесса итераций обычно берут условие [math]\left \| x^{(k+1)} - x^{(k)} \right \| \lt \varepsilon[/math], где [math]\varepsilon[/math] - требуемая точность решения.

Основная сложность метода Ньютона заключается в обращении матрицы Якоби. Вводя обозначение [math]\Delta x^{(k)} = x^{(k+1)} - x^{(k)}[/math] получаем СЛАУ для вычисления [math]\Delta x^{(k)}:[/math] [math]\frac{\partial{F(x^{(k)})}}{\partial{x}} = -F(x^{(k)})[/math]

Тогда [math]x^{(k+1)} = x^{(k)}+ \Delta x^{(k)}.[/math]

Часто метод Ньютона модифицируют следующим образом. По ходу вычислений или заранее выбирают возрастающую последовательность чисел [math]n_0=0, n_1,\ldots[/math]

При [math]n_i \le k \lt n_{i+1}[/math] вычисление [math]\Delta x^{(k)}[/math] осуществляют по следующей формуле:

[math]\frac{\partial{F(x^{n_i})}}{\partial{x}} = -F(x^{(k)}).[/math]

Увеличение числа итераций, сопровождающее такую модификацию, компенсируется «дешевизной» одного шага итерации.

1.3 Вычислительное ядро алгоритма

Основная вычислительная нагрузка алгоритма заключается в решении СЛАУ:

[math]\frac{\partial F(x^{(k)})}{\partial x}\Delta x^{(k)} = -F(x^{(k)}) \qquad (1)[/math]

Для нахождения [math]\Delta x^{(k)}[/math], по которому вычисляется значение вектора [math]\overline{x}[/math] на очередной итерации: [math]x^{(k+1)} = x^{(k)} + \Delta x^{(k)}.[/math]

1.4 Макроструктура алгоритма

Как уже было сказано, основную часть каждой итерации метода составляет нахождение матрицы Якоби и решение СЛАУ [math](1)[/math] для нахождения [math]\Delta x^{(k)}.[/math]

1.5 Схема реализации последовательного алгоритма

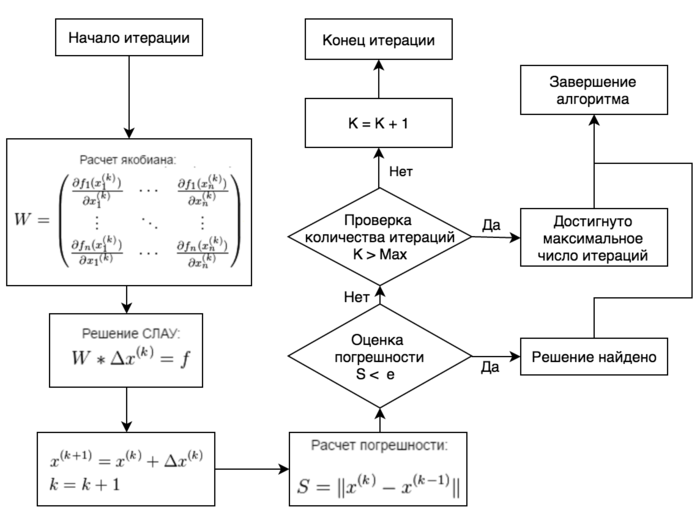
Формулы метода описаны выше. На рис 1. представлена блок-схема алгоритма, в которой:

1. [math]n[/math] - число уравнений в СЛАУ
2. Max - предельное число итераций
3. [math]\varepsilon[/math] - точность вычислений
4. [math]x^{(0)}[/math] - начальное приближение

Рис.1 Блок-схема последовательного алгоритма

1.6 Последовательная сложность алгоритма

Пусть вычисление значения первой производной функции [math]f_i(x_1,x_2,\ldots,x_n)[/math] в точке [math]x^{(k)}[/math] имеет оценку сложности [math]D_i[/math], решение СЛАУ [math](1)[/math] имеет оценку сложности [math]S[/math] (в эту оценку также включаются операции по нахождению элементов матрицы Якоби), а оценка сложности сложения векторов – [math]V[/math]. Тогда оценка сложности одной итерации представляется в виде:

[math]\sum^{n}_{i=1} {D_i} + S + V[/math]

Количество итераций определяется скоростью сходимости алгоритма. Скорость сходимости метода Ньютона в общем случае является квадратичной. Однако успех или неуспех применения алгоритма во многом определяется выбором начального приближения решения. Если начальное приближение выбрано достаточно хорошо и матрица системы линейных уравнений на каждой итерации хорошо обусловлена и имеет обратную матрицу, то метод Ньютона сходится к единственному в данной окрестности решению. На практике критерием работоспособности метода является число итераций: если оно оказывается большим (для большинства задач >100), то начальное приближение выбрано плохо.

В качестве примера можно рассмотреть алгоритм Ньютона, использующий для решения СЛАУ метод Гаусса. Рассмотрим решение системы, для которой справедливы следующие предположения:

• Вычисление значения каждой функции в заданной точке требует [math]O(n)[/math] операций.
• Вычисление значения производной каждой функции в заданной точке требует [math]O(n)[/math] операций.

В таких предположениях указанное выражение для вычисления сложности примет следующий вид:

[math]O(n^2) + O(n^3) + O(n) = O(n^3)[/math]

Предположим также, что выполнены все условия для квадратичной сходимости метода, и для решения системы потребуется небольшое (<100) количество итераций.

Пусть алгоритм сойдется за [math]L[/math] итераций, тогда итоговая сложность будет равна [math]O(L \cdot n^3)[/math].

1.7 Информационный граф

Рис.2 Информационный граф алгоритма

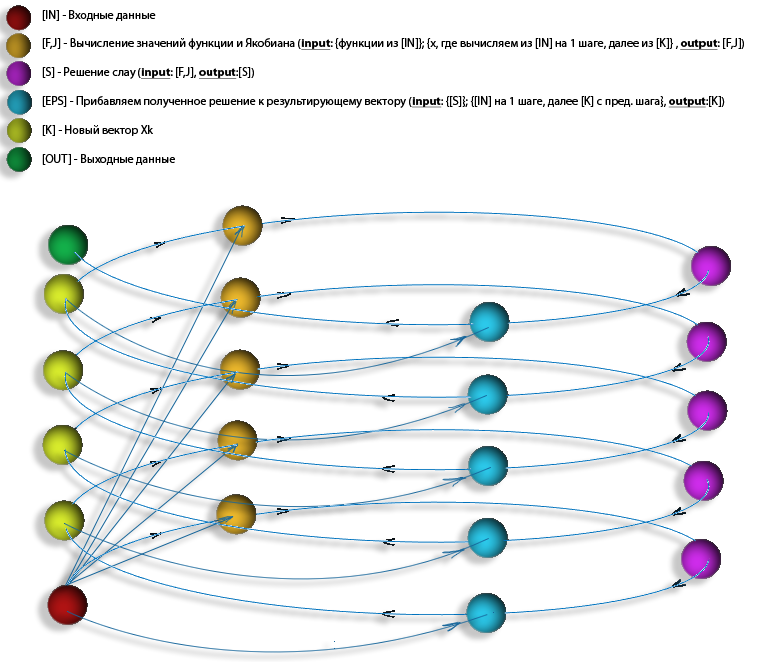
На рис. 2 изображена структура информационного графа алгоритма. Блок IN представляет собой выбор начального приближения, необходимой точности. Каждый блок IT соответствует одной итерации алгоритма, блок-схема итерации алгоритма представлена на рис. 3. Блок OUT соответствует успешному окончанию алгоритма.

Как видно, алгоритм является строго последовательным, каждая итерация зависит от результата предыдущей.

Рис.3 Блок-схема итерации алгоритма

Информационный граф метода Ньютона может быть также представлен в виде следующего рисунка:

Рис.4 Информационный граф алгоритма.

1.8 Ресурс параллелизма алгоритма

Хотя сам по себе алгоритм и является строго последовательным, в нем все же присутствует возможность ускорить выполнение за счет распараллеливания отдельных этапов. Основной ресурс параллелизма заключен в решении СЛАУ [math](1)[/math]. Применять можно любой из известных алгоритмов, ориентируясь на известные особенности структуры матрицы Якоби исходной системы.

В качестве примера рассмотрим метод Ньютона, использующий для решения СЛАУ параллельный вариант метода Гаусса, в котором между процессорами распределяются строки исходной матрицы. Оставаясь в тех же предположениях, что были сделаны при вычислении оценки последовательной сложности, получим оценку параллельной сложности алгоритма.

Пусть задача решается на [math]p[/math] процессорах, тогда сложность решения СЛАУ имеет оценку [math]O(\frac{n^3}{p})[/math].

Теперь каждому процессору нужно вычислить не [math]n[/math], а [math]\frac{n}{p}[/math] функций, поэтому для вычисления элементов матрицы Якоби и правой части СЛАУ потребуется [math]O(\frac{n^2}{p})[/math] операций.

Таким образом, получаем следующую оценку параллельной сложности одной итерации алгоритма: [math]O(\frac{n^2}{p}) + O(\frac{n^3}{p}) + O(n) = O(\frac{n^3}{p})[/math].

Пусть алгоритм сходится за [math]L[/math] итераций, тогда итоговая сложность будет равна [math]O(L \cdot \frac{n^3}{p})[/math].

1.9 Входные и выходные данные алгоритма

При определении объема входных и выходных данных алгоритма будем придерживаться следующих предположений:

• Рассматривается 64-битная система, таким образом каждый адрес занимает 64 бита.
• Все числа, с которыми оперирует алгоритм также занимают 64 бита.
• Каждая функция будет представлена своим адресом, таким образом вклад функций в объем входных данных будет равен [math]n[/math] чисел.
• Производная каждой функции также представлена своим адресом, и вклад производных в объем входных данных будет равен [math]n^2[/math] чисел.

Входными данными алгоритма являются:

1. Функции, образующие систему уравнений.
2. Производные функций, образующих систему уравнений, если их можно задать аналитически.
3. Точность, с которой требуется найти решение.
4. Максимальное число итераций, которое может быть проделано.
5. Начальное приближение [math]x^{(0)}[/math].

Объем входных данных алгоритма равен [math]n ^2 + 2\cdot n + 2 [/math] в случае, когда на вход алгоритму передаются частные производные ([math]n^2[/math] адресов частных производных [math]n[/math] функций по [math]n[/math] переменным, [math]n[/math] адресов функций, образующих систему уравнений, [math]n[/math]-мерный вектор начального приближения, требуемая точность и максимальное количество итераций), когда частные производные приближенно вычисляются непосредственно в программе, объем входных данных равен [math]2\cdot n + 2.[/math]

Выходными данными алгоритма в случае успеха является вектор, который удовлетворяет решению СЛАУ с заданной точностью, в случае выхода количества итераций за заданное ограничение, считается, что алгоритм не смог найти удовлетворяющее ограничениям решение, и выдается сообщение об ошибке.

Объем выходных данных: [math]n.[/math]

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложностей зависит от того, какие алгоритмы применяются для решения СЛАУ [math](1)[/math]. Результат работы алгоритма сильно зависит от выбора начального приближения решения. При удачном выборе алгоритм достаточно быстро сходится к искомому решению. Глобальная сходимость для многих задач отсутствует.

Существует теорема о достаточном условии сходимости метода Ньютона:

Пусть функция [math]F(x)[/math] непрерывно дифференцируема в открытом выпуклом множестве [math]G \subset {\mathbb R}^n[/math]. Предположим, что существуют [math]\overline{x^*} \in {\mathbb R}^n[/math] и [math]r,\beta \gt 0 [/math], такие что [math]N(\overline{x^*},r) \subset G , F(\overline{x^*}) = 0[/math] , и существует [math]W^{-1}(\overline{x^*})[/math], причем [math]\left \| W^{-1}(\overline{x^*})\right \| \le \beta [/math] и [math]W(x) \in Lip_{\gamma} (N(\overline{x^*},r))[/math]. Тогда существует [math]\varepsilon \gt 0[/math] такое, что для всех [math]x^{(0)} \in N(\overline{x^*}, \varepsilon)[/math] последовательность [math]x^{(1)},x^{(2)},\ldots[/math] порождаемая итерационным процессом сходится к [math]\overline{x^*}[/math] и удовлетворяет неравенству [math]\left \|x^{(k+1)} - \overline{x^*}\right \| \le \beta\cdot\gamma\cdot{\left \| x^{(k)}- \overline{x^*}\right \|}^2[/math].

Использовались следующие обозначения:

• [math]N(x,r)[/math] - открытая окрестность радиуса [math]r[/math] с центром в точке [math]x[/math];

• [math]W(x) \in Lip_{\gamma}(N(x,r))[/math] означает, что [math]W(x)[/math] непрерывна по Липшицу с константой [math]\gamma[/math] в области [math]N(x,r)[/math].

Оставаясь в предположениях, описанных при вычислении объема входных данных, имеем объем входных данных равный [math]n^2 + 2\cdot n + 2 = O(n^2)[/math] чисел.

Оценку числа операций возьмем для реализации метода Ньютона с помощью метода Гаусса: [math]O(n^3)[/math]. Тогда вычислительная мощность есть [math]O(n)[/math].