Poisson equation, solving with DFT, scalability
Основные авторы описания: В.М.Степаненко, Е.В.Мортиков.
Содержание
1 Ссылки
Для проведения экспериментов использовалась реализация алгоритма решения уравнения Пуассона дискретным преобразованием Фурье.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [4 : 100] со значениями квадрата целого числа;
- размер области [100x100x100 : 250x100x100] с шагом 50x100x100.
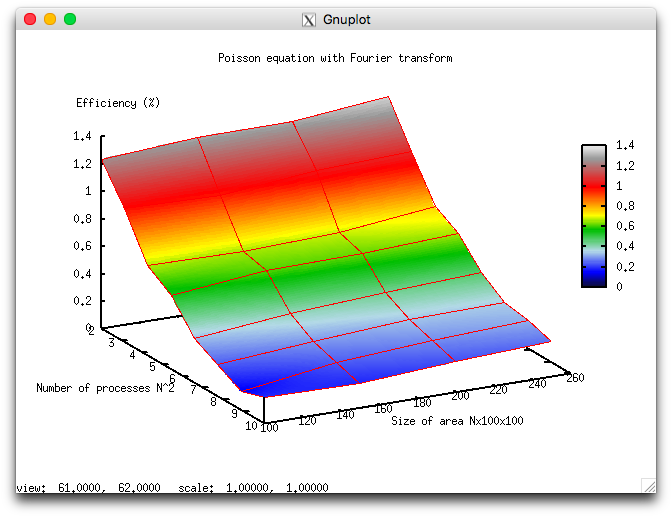
В результате проведенных экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0,132%;
- максимальная эффективность реализации 1,34%.
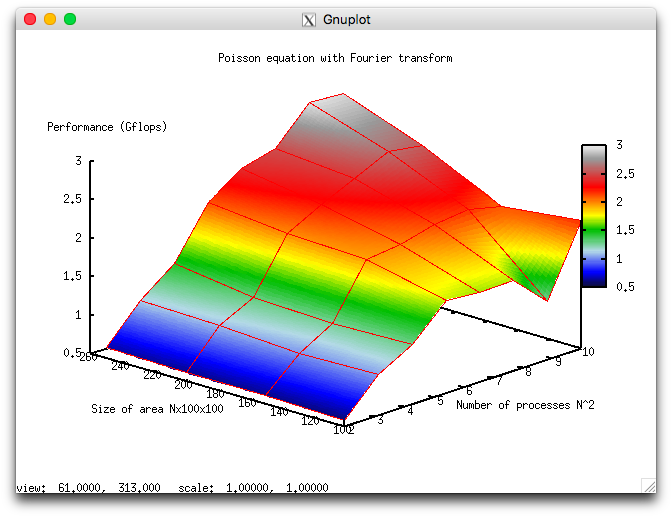
На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.
Приведенные результаты хорошо качественно согласуются с оценками, приведенными в предыдущем разделе. Так, на рис.8 видно, что с ростом N масштабируемость алгоритма повышается - производительность алгоритма быстрее растет с ростом числа ядер. Это согласуется с уменьшением \alpha при увеличении N, хотя выражение \alpha=12/(6\log_2 N+1) дает значительно более слабую зависимость. В целом же, алгоритм масштабируется достаточно слабо: при максимальном из задаваемых размеров области 250х100х100 при росте числа ядер в 25 раз (от 4 до 100), производительность вычислений вырастает только в 6 раз.
4 Динамические характеристики и эффективность реализации алгоритма
Все результаты получены на суперкомпьютере "Ломоносов". Использовались процессоры Intel Xeon X5570 с пиковой производительностью в 94 Гфлопс, а также компилятор 13.1.0. На рисунках показана эффективность реализации алгоритма решения уравнения Пуассона дискретным преобразованием Фурье на 64 процессах.
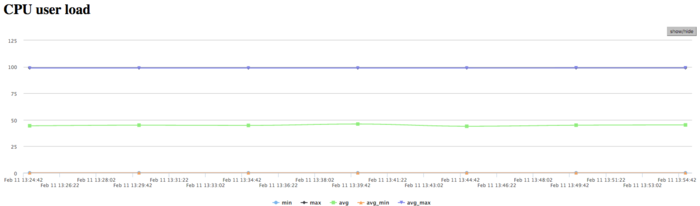
На графике загрузки процессора видно, что почти все время работы программы уровень загрузки составляет около 50%. Это указывает на равномерную загруженность вычислениями процессоров, при использовании 8 процессов на вычислительный узел и без использования Hyper Threading.
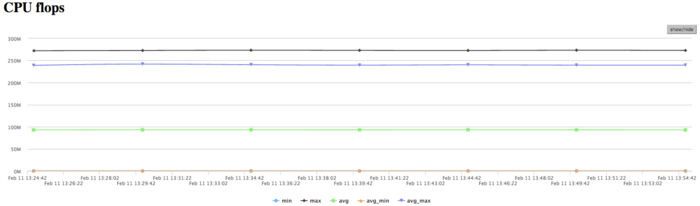
На Рисунке 4 показан график количества операций с плавающей точкой в секунду. На графике видна общая низкая производительность вычислений около 250 Мфлопс в пике и около 100 Мфлопс в среднем по всем узлам. Это указывает не дисбаланс вычислений.
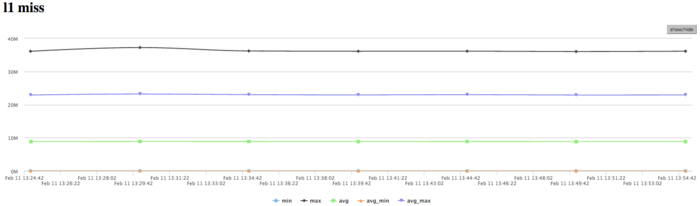
На графике кэш-промахов первого уровня видно, что число промахов достаточно большое для нескольких ядер и находится на уровне 25 млн/сек (в пике до 40 млн/сек), что указывает на интенсивные вычисления в части процессов. В среднем по всем узлам значения значительно ниже (около 9 млн/сек). Это указывает на неравномерное распределение вычислений.
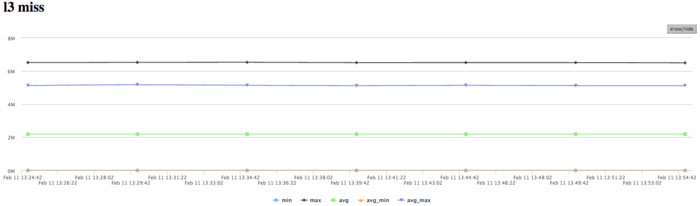
На графике кэш-промахов третьего уровня видно, что число промахов все еще достаточно большое и находится на уровне 5 млн/сек, однако в среднем по всем узлам значения около 2 млн/сек. Соотношение кэш промахов L1|L3 для процессов с высокой производительностью доходит до 9, однако в среднем около 4,5. Это указывает на достаточно хорошую локальность вычислений у части процессов, и возможно это и есть причина их высокой производительности. Для большинства процессов соотношение типично для такого класса задач.
На графике чтений из памяти на наблюдается неравномерная активность чтения из памяти процессами: несколько читают очень активно, остальные используют значительно менее эффективно. Однако активность тех нескольких процессов чтения из памяти достаточно высока, что в сочетании с показаниями достаточно высокого уровня кэш-промахов указывает на достаточно большой процент промахов из кэш в оперативную память.
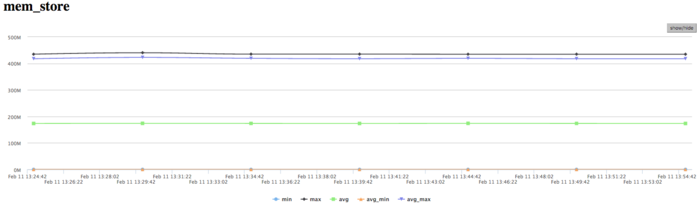
На графике записей в память видна похожая картина неравномерности вычислений, при которой одновременно активно выполняют запись только несколько процессов. Это коррелирует с другими графиками выполнения и указывает на низкую эффективность данной реализации. Стоит отметить, достаточно низкое число обращений на запись в память. Это указывает на хорошую организацию вычислений, и достаточно эффективную работу с памятью.
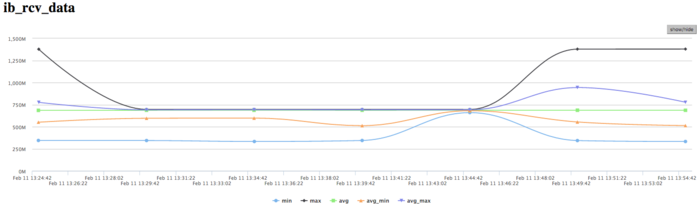
На графике скорости передачи данных по сети Infiniband наблюдается достаточно высокая скорость передачи данных в байтах в секунду. Это говорит о том, что процессы между собой обмениваются интенсивно и вероятно достаточно крупными порциями данных. Стоит отметить, что скорость передачи отличается между процессами, что указывает на дисбаланс вычислений.
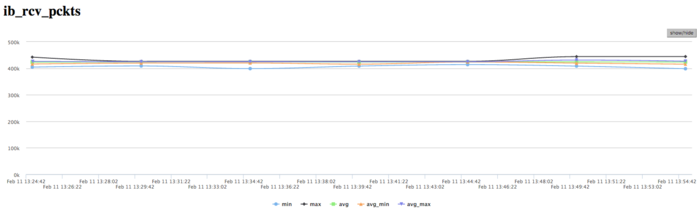
На графике скорости передачи данных в пакетах в секунду наблюдается очень высокая интенсивность передачи данных выраженная в пакетах в секунду. Это говорит о том, что, вероятно, процессы обмениваются существенными объемами данных, но очень интенсивно. Так же наблюдается почти отсутсвующий дизбаланс между процессами чем наблюдаемый в графиках использования памяти и вычислений и передачи данных в байтах/сек. Это указывает на то, что процессы обмениваются по алгоритму одинаковым числом пакетов, однако получают разные объемы данных и ведут неравномерные вычисления.
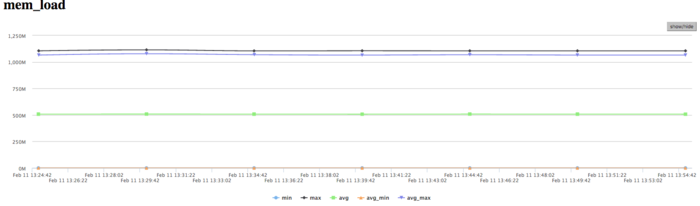
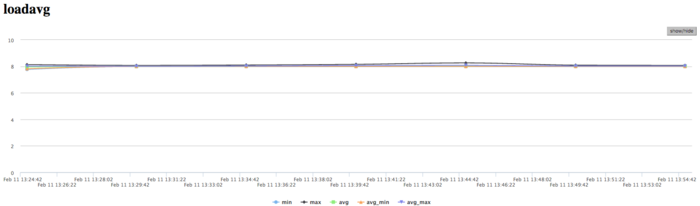
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 8. Это свидетельствует о стабильной работе программы с загруженными вычислениями всеми узлами. Это указывает на очень рациональную и статичную загрузку аппаратных ресурсов процессами. И показывает достаточно хорошую эффективность выполняемой реализации. В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала достаточно эффективно, и стабильно. Использование памяти интенсивное, а использование коммуникационной среды очень высоко интенсивное, при этом объемы передаваемых данных являются достаточно высокими. Это указывает на требовательность к коммуникационной среде алгоритмической части программы. Низкая эффективность связана судя по всему с достаточно высоким объемом пересылок на каждом процессе, интенсивными обменами сообщениями.