Полный метод циклической редукции
| Циклическая редукция для трёхдиагональной матрицы, точечный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n)[/math] |
| Объём входных данных | [math]4n-2[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(log n)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Циклическая редукция - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида [math]Ax = b[/math], где
- [math] A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}, b = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix} [/math]
Бывает, однако, что при изложении сути методов решения трёхдиагональных СЛАУ[3] элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид
- [math] A = \begin{bmatrix} b_{1} & a_{1} & 0 & \cdots & \cdots & 0 \\ c_{2} & b_{2} & a_{2} & \cdots & \cdots & 0 \\ 0 & c_{3} & b_{3} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & c_{n-1} & b_{n-1} & a_{n-1} \\ 0 & \cdots & \cdots & 0 & c_{n} & b_{n} \\ \end{bmatrix}\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix} = \begin{bmatrix} f_{1} \\ f_{2} \\ \vdots \\ f_{n} \\ \end{bmatrix} [/math]
или, если записывать отдельно по уравнениям, то
[math]b_{1} x_{1} + a_{1} x_{2} = f_{1}[/math],
[math]c_{i} x_{i-1} + b_{i} x_{i} + a_{i} x_{i+1} = f_{i}, 2 \le i \le n-1[/math],
[math]c_{n} x_{n-1} + b_{n} x_{n} = f_{n}[/math].
Циклическая редукция, как и все варианты прогонки, заключается [3][4] в исключении из уравнений неизвестных, однако, в отличие от них, в ней исключение ведут одновременно по всей СЛАУ. В принципе, её можно считать вариантом метода редукции, выполняемого максимально возможное для данной СЛАУ число раз.
1.2 Математическое описание алгоритма
Лучше всего схема циклической редукции[3] разработана для случая [math]n = 2^{m}-1[/math]. Эта схема состоит из прямого и обратного ходов. Прямой ход состоит из последовательного уменьшения в СЛАУ количества уравнений почти в 2 раза (за счёт подстановки из уравнений с нечётными номерами заменяются уравнения с чётными), пока не останется одно уравнение, обратный - в получении всё большего количества компонент решения исходной СЛАУ. Оба хода - как прямой, так и обратный - разбиты на шаги. Здесь мы приведём тот вариант алгоритма, в котором операции экономятся за счёт предварительной нормировки уравнений, используемых для исключения неизвестных.
1.2.1 Прямой ход редукции
В начале считается, что все [math]c^{(0)}_{i} = c_{i}, b^{(0)}_{i} = b_{i}, a^{(0)}_{i} = a_{i}, f^{(0)}_{i} = f_{i}, x^{(0)}_{i} = x_{i}[/math]
На k-м шаге теперь выполняем процедуру редукции системы уравнений размерности n.
Для каждого из уравнений
[math]c^{(k)}_{i} x^{(k)}_{i-1} + b^{(k)}_{i} x^{(k)}_{i} + a^{(k)}_{i} x^{(k)}_{i+1} = f^{(k)}_{i}[/math]
с нечётными [math]i[/math] с помощью деления уравнения на [math]b^{(k)}_{i}[/math] выполняется его замена на уравнение
[math] (c^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i-1} + x^{(k)}_{i} + (a^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i+1} = f^{(k)}_{i}/b^{(k)}_{i}[/math]
Уравнение
[math]b^{(k)}_{1} x^{(k)}_{1} + a^{(k)}_{1} x^{(k)}_{2} = f^{(k)}_{1}[/math]
аналогично меняется на уравнение
[math]x^{(k)}_{1} + (a^{(k)}_{1}/b^{(k)}_{1}) x^{(k)}_{2} = f^{(k)}_{1}/b^{(k)}_{1}[/math]:
а уравнение
[math]c^{(k)}_{n} x^{(k)}_{n-1} + b^{(k)}_{n} x^{(k)}_{n} = f^{(k)}_{n}[/math]
меняется на уравнение
[math](c^{(k)}_{n}/b^{(k)}_{n}) x^{(k)}_{n-1} + x^{(k)}_{n} = f^{(k)}_{n}/b^{(k)}_{n}[/math]:
Для каждого же из уравнений
[math]c^{(k)}_{i} x^{(k)}_{i-1} + b^{(k)}_{i} x^{(k)}_{i} + a^{(k)}_{i} x^{(k)}_{i+1} = f^{(k)}_{i}[/math]
с чётными [math]i[/math] (кроме [math]2[/math] и [math]n-2[/math]) выполняется, с учётом [math]x^{(k+1)}_{i/2} = x^{(k)}_{i}[/math] его замена на уравнение
[math]c^{(k+1)}_{i/2} x^{(k+1)}_{(i-2)/2} + b^{(k+1)}_{i/2} x^{(k+1)}_{i/2} + a^{(k+1)}_{i/2} x^{(k+1)}_{(i+2)/2} = f^{(k+1)}_{i/2}[/math]
при этом
[math]c^{(k+1)}_{i/2} = - c^{(k)}_{i}(c^{(k)}_{i-1}/b^{(k)}_{i-1})[/math],
[math]a^{(k+1)}_{i/2} = - a^{(k)}_{i}(a^{(k)}_{i+1}/b^{(k)}_{i+1})[/math],
[math]b^{(k+1)}_{i/2} = b^{(k)}_{i} - c^{(k)}_{i}(a^{(k)}_{i-1}/b^{(k)}_{i-1}) - a^{(k)}_{i}(c^{(k)}_{i+1}/b^{(k)}_{i+1})[/math],
[math]f^{(k+1)}_{i/2} = f^{(k)}_{i} - c^{(k)}_{i}f^{(k)}_{i-1}/b^{(k)}_{i-1} - a^{(k)}_{i}f^{(k)}_{i-1}/b^{(k)}_{i-1}[/math].
Для 2го уравнения выполняется его замена на уравнение
[math]b^{(k+1)}_{1} x^{(k+1)}_{1} + a^{(k+1)}_{1} x^{(k+1)}_{(2} = f^{(k+1)}_{1}[/math]
при этом
[math]a^{(k+1)}_{1} = - a^{(k)}_{2}(a^{(k)}_{3}/b^{(k)}_{3})[/math],
[math]b^{(k+1)}_{1} = b^{(k)}_{2} - c^{(k)}_{2}(a^{(k)}_{1}/b^{(k)}_{1}) - a^{(k)}_{2}(c^{(k)}_{3}/b^{(k)}_{3})[/math],
[math]f^{(k+1)}_{1} = f^{(k)}_{2} - c^{(k)}_{2}f^{(k)}_{1}/b^{(k)}_{1} - a^{(k)}_{2}f^{(k)}_{1}/b^{(k)}_{1}[/math]
[math]n-1[/math]-е уравнение заменяется на
[math]c^{(k+1)}_{(n-1)/2} x^{(k+1)}_{(n-3)/2} + b^{(k+1)}_{(n-1)/2} x^{(k+1)}_{(n-1)/2} = f^{(k+1)}_{(n-1)/2}[/math]
при этом
[math]c^{(k+1)}_{(n-1)/2} = - c^{(k)}_{n-1}(c^{(k)}_{n-2}/b^{(k)}_{n-2})[/math],
[math]b^{(k+1)}_{(n-1)/2} = b^{(k)}_{n-1} - c^{(k)}_{n-1}(a^{(k)}_{n-2}/b^{(k)}_{n-2}) - a^{(k)}_{n-1}(c^{(k)}_{n}/b^{(k)}_{n})[/math],
[math]f^{(k+1)}_{(n-1)/2} = f^{(k)}_{n-1} - c^{(k)}_{n-1}f^{(k)}_{n-2}/b^{(k)}_{n-2} - a^{(k)}_{n-1}f^{(k)}_{n-2}/b^{(k)}_{n-2}[/math].
По окончании всех этих манипуляций размерность k+1-й СЛАУ оказывается равной [math](n-1)/2[/math].
Шаги повторяются до тех пор, пока после [math]m-1[/math] шагов редукции размерность СЛАУ не становится равной 1 и остаётся одно уравнение
[math]b^{(m-1)}_{1} x^{(m-1)}_{1} = f^{(m-1)}_{1}[/math]
1.2.2 Обратный ход редукции
Из последнего уравнения, полученного прямым ходом, вычисляется
[math]x^{(m-1)}_{1} = f^{(m-1)}_{1}/b^{(m-1)}_{1}[/math]
Теперь, последовательно уменьшая верхние индексы неизвестных, используется нечётные уравнения каждого шага для вычисления неизвестных с соотвествующими нечётными номерами. Чётные неизвестные получаются из тождеств [math]x^{(k)}_{i} = x^{(k+1)}_{i/2}[/math], а для нечётных [math]i[/math]
[math]x^{(k)}_{i} = f^{(k)}_{i}/b^{(k)}_{i} - (c^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i-1} - (a^{(k)}_{i}/b^{(k)}_{i}) x^{(k)}_{i+1} [/math]
c "левого края" системы будет
[math]x^{(k)}_{1} = f^{(k)}_{1}/b^{(k)}_{1} - (a^{(k)}_{1}/b^{(k)}_{1}) x^{(k)}_{2}[/math]
а с "правого"
[math]x^{(k)}_{n} = f^{(k)}_{n}/b^{(k)}_{n} - (c^{(k)}_{n}/b^{(k)}_{n}) x^{(k)}_{n-1}[/math]
После вычисления всех [math]x^{(0)}_{i}[/math] значения искомых неизвестных [math]x_{i} = x^{(k)}_{i}[/math].
1.3 Вычислительное ядро алгоритма
Видно, что, поскольку вычисляемые на каждом шаге прямого хода редукции при преобразовании нечётных уравнений отношения коэффициентов
[math] c^{(k)}_{i}/b^{(k)}_{i} , a^{(k)}_{i}/b^{(k)}_{i} , f^{(k)}_{i}/b^{(k)}_{i}[/math]
почти все используются для преобразований двух чётных уравнений, то при выделении "микровычислений", из которых следует составить шаги редукции и которые составляют его ядро, лучше отнести вычисления этих отношений к предыдущему шагу редукции. Таким образом, на "подготовительном шаге" микроядро будет для каждого [math]i[/math] состоять только из трёх делений (кроме [math]2[/math] и [math]n[/math] - там будет по 2 деления), а затем на каждом последующем шаге редукции для каждого [math]i[/math] - из двух умножений и двух вычислений выражений типа [math]a-bc-de[/math], с последующими тремя делениями (на "краях" часть этих операций отсутствует или урезана, но общую картину это не очень меняет).
Что касается шагов обратного хода, то там для каждого [math]i[/math] рано или поздно выполняется одна операция типа [math]a-bc-de[/math] (на "краях" - типа [math]a-bc[/math]).
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
Метод циклической редукции изначально спроектирован для параллельного исполнения, поскольку является по отношению к, например, классической прогонке, алгоритмом с избыточными вычислениями. Поэтому смысла в его последовательной реализации не очень много и они не встречаются в библиотеках программ.
1.6 Последовательная сложность алгоритма
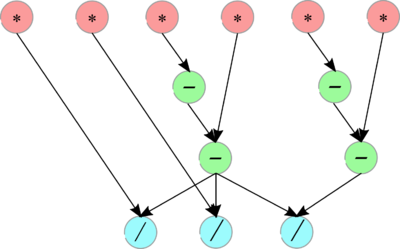
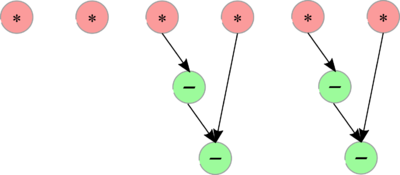
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Литература
- ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
- ↑ Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
- ↑ 3,0 3,1 3,2 Ильин В.П., Кузнецов Ю.И. Трехдиагональные матрицы и их приложения. М.: Наука. Глав-ная редакция физико-математической литературы, 1985г., 208 с.
- ↑ Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Параллельные вычислительные технологии (ПаВТ’2016): труды международной научной конференции (г. Архангельск, 28 марта – 1 апреля 2016 г.). Челябинск: Издательский центр ЮУрГУ, 2016. С. 347-360.