Уровень алгоритма

Алгоритм Качмажа

Материал из Алговики
Перейти к навигации Перейти к поиску


Алгоритм Качмажа (S. Kaczmarz)
Последовательный алгоритм
Последовательная сложность [math]k \cdot O(n)[/math], где [math]k[/math] - количество итераций
Объём входных данных система линейных алгебраических уравнений ([math]m[/math] уравнений) с [math]n[/math] неизсветными, где [math]m \geq n[/math]; [math]m \cdot n + m + n[/math] ячеек ОЗУ.
Объём выходных данных приближенное решение: [math]n[/math] ячеек ОЗУ


Основные авторы описания: Е.С. Козлова, А.А. Иванов.

Синонимы названия алгоритма: метод алгебраической реконструкции, Algebraic Reconstruction Technique, Projection onto Convex Sets.

Содержание

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Метод алгебраической реконструкции полностью последовательный строковый (row-action method) метод с длинной историей, богато описанный в литературе. В классическом виде метод был впервые сформулирован и предложен польским математиком С. Качмажем (Stefan Kaczmarz) для решения систем линейных алгебраических уравнений с квадратными и невырожденными матрицами, а в последствии независимо был использован Р. Гордоном и др. (R. Gordon; R. Bender; Herman) для реконструкции изображений по их проекционным данным в задаче рентгеновской компьютерной томографии.

В более общем случае последовательность, полученная по методу итераций С. Качмажа, также сходится к решению и для переопределенных, но обязательно совместных с.л.а.у. (систем линейных алгебраических уравнений). На каждой итерации алгоритма используется только одно уравнение с.л.а.у., но в результате пересчитывается каждая компонента приближенного решения на данной итерации.

Далее представим наивный вывод итерационного метода следуя общим представлениям. Запишем с.л.а.у. с невырожденной матрицей коэффициентов [math]A \cdot u=f,\, A\in R^{n\times n},\, u\in R^{n},\, f\in R^{n}[/math]. Проследим процедуру минимизации с использованием метода оптимального координатного спуска, описанную, например, в [1]. Рассмотрим функцию ошибки: [math]\Phi\left(u\right)=\Vert u_{*}-u\Vert^{2}[/math], где [math]u_{*}[/math] - единственное решение системы в смысле метода наименьших квадратов.

Будем искать решение системы на некотором линейном подпространстве [math]\Lambda\left(\varphi_{1},\ldots,\varphi_{p}\right)[/math] в виде итерационной последовательности: [math]u^{0}=\Theta,\, u^{k+1}=u^{k}\,+\, C_{k}\varphi_{j\left(k\right)}[/math], где [math]j\left(k\right)\in\left\{ 1,2,\ldots,p\right\}[/math], а [math]C_{k}[/math] - некоторый неизвестный коэффициент. Легко заметить, что [math]\Phi\left(u^{k+1}\right)=\Vert u_{*}-u^{k+1}\Vert^{2}=\Vert u_{*}-u^{k}-C_{k}\varphi_{j\left(k\right)}\Vert^{2}[/math]

Обозначим вектор [math]z^{k}=u_{*}-u^{k}[/math] - вектор ошибок приближения решения с.л.а.у. на шаге с номером [math]k[/math]. Предположим также, что [math]\Vert\varphi_{i}\Vert=1,\,\forall i[/math]. С учетом этого: [math]\Phi\left(u^{k+1}\right)=\Vert z^{k}-C_{k}\varphi_{j\left(k\right)}\Vert^{2}=\Vert z^{k}\Vert^{2}-2C_{k}\left(z^{k},\varphi_{j\left(k\right)}\right)+C_{k}^{2}[/math].

Продифференцируем последнее уравнение по [math]C_{k}[/math] и приравняем к нулю, в результате получим, что [math]C_{k}=\left(z^{k},\varphi_{j\left(k\right)}\right)[/math].

Возвращаясь к с.л.а.у., пусть вектора в линейной оболочке [math]\Lambda[/math] выбраны как [math] \varphi_{i}=\frac{a_{i}}{\Vert a_{i}\Vert}[/math], тогда [math]\left(z^{k},a_{j\left(k\right)}\right)=f_{j\left(k\right)}-a_{j\left(k\right)}^{T}u^{k}[/math] и последовательность приобретает законченный вид, основная формула алгоритма:

[math]u^{k+1}=u^{k}+\frac{f_{j\left(k\right)}-\left(a_{j\left(k\right)},u^{k}\right)}{\Vert a_{j\left(k\right)}\Vert^{2}}a_{j\left(k\right)}[/math].

Мы показали достаточно наивное построение алгоритма, которое не доказывает ни факт сходимости ни тем более к решению задачи - это предмет доказательства теоремы о сходимости при определенном задании отображения [math]j\left(k\right)[/math] (при построении мы не накладывали на него никаких ограничений). Однако данное построение позволяет проследить идею о минимизации ошибки решения (а не невязки с.л.а.у.) и связь алгоритма Качмажа с методом координатного спуска по векторам [math]\varphi_{i}[/math].

Все дальнейшие модификации данной формулы, а, соответсвенно, и самого алгоритма, основаны на:

  • введения параметра т.н. релаксации,
  • экзотических способах задания отображения [math]j\left(k\right)[/math],
  • выборе специальных критериев останова итераций,
  • переходе к блочным модификациям.

1.2 Библиография

Стефан Качмаж - польский математик, родился 1895 г. в городе Самбор (Sambor) Галиция (Galicia), Австро-Венгрия (Austria-Hungary), ныне Украина. Стефан Качмаж был профессором математики на факультете машиностроения университета Яна Казимира (Jan Kazimierz University) в городе Львов (Lwów) с 1919 по 1939 год, там же сотрудничал с Стефаном Банахом. Предложенный им итерационный метод решения с.л.а.у. послужил основой для многих современных технологий в обработке изображений, в том числе в задачах компьютерной томографии [2].

Применение метода С. Качмажа или т.н. метода алгебраической реконструкции наиболее известно в задачах реконструктивной компьютерной томографии высокого разрешения. Для интерпретации данных, полученных в результате неразрушающего сканирования некоторого объекта, с 60-70-х годов применяются различные аппаратные и программные реализации итерационного метода, разработанного польским математиком С. Качмажем (S. Kaczmarz) в 1937 году[3]; этот метод был использован Г. Хаусфилдом (G.N. Hounsfield) - конструктором первого томографа «ЭМИ-сканнер»[4] (нобелевская премия по физиологии и медицине в 1979 году).

Так же данный метод можно часто встретить под следующими названиями: Algebraic Reconstruction Technique (ART)[5][6][7], Projection onto Convex Sets (PCS)[8], Kaczmarz Algorithm [9] или метод ортогональных проекций.

Конструированию различных алгоритмов на основе итераций С. Качмажа посвящено существенное количество работ: согласно исследованию польского математика и библиографа А. Сигелски (A. Cegielski), на начало 2010 года статья С. Качмажа цитируется более чем в четырехстах реферируемых и значимых публикациях ученых из различных областей знаний. В Советской и Российской научных школах исследования итераций С. Качмажа представлены в литературе такими известными учеными как: В.Н. Ильин, Г.П. Васильченко, А.А. Светлаков и другие, например, в работах[10][11]. Общие идеи о проекционных методах так же представлены в классической работе Л. Г. Гурина, Б. Т. Поляка, Э. В. Райка[12], где впервые предлагается и обосновывается идентичный алгоритм для решения систем линейных алгебраических неравенств и уравнений.

В 2008 году американскими математиками Т. Штромером (T. Strohmer) и Р. Вершининым (R. Vershynin) в [13] была предложена рандомизированная модификация итерационного метода, в которой последовательность приближений к решению для совместных и переопределенных с.л.а.у. сходится с экспоненциальной скоростью.

Множество модификаций идеи метода ортогональных проекций нашли свое практическое применение в различных областях знаний, связанных с обработкой и интерпретацией больших объемов данных: при реконструкции синограмм в медицине, биологии, геологии; при решении задач диагностики плазмы, кристаллографии[14], дефектоскопии и микроскопии, параллельных вычислений и распределенного анализа[15] и др.

1.3 Математическое описание алгоритма

1.3.1 Математическое описание

Запишем совместную (в общем случае - переопределенную) с.л.а.у.

[math]Au=f,\, A\in \mathbb{R}^{m\times n},\, u\in \mathbb{R}^{n},\, f\in \mathbb{R}^{m},[/math]

тогда итерации согласно алгоритму определяются последовательностью

[math]u^{k+1}=u^{k}+\lambda_{k}\frac{f_{j\left(k\right)}-\left(a_{j\left(k\right)},u^{k}\right)}{\Vert a_{j\left(k\right)}\Vert^{2}}a_{j\left(k\right)},[/math]

где

[math]A=\left(a_{1},\, a_{2},\,\ldots\,,\, a_{m}\right)^{T}\in \mathbb{R}^{m\times n},\, u\in \mathbb{R}^{n},\, f=\left(f_{1},\, f_{2},\,\ldots\,,\, f_{m}\right)\in \mathbb{R}^{m},[/math]

а последовательность проектирования в классическом варианте алгоритма определяется как

[math]j\left(k\right)=\left(k\ \bmod\ m\right)+1,\, k=\overline{0,\infty},[/math]

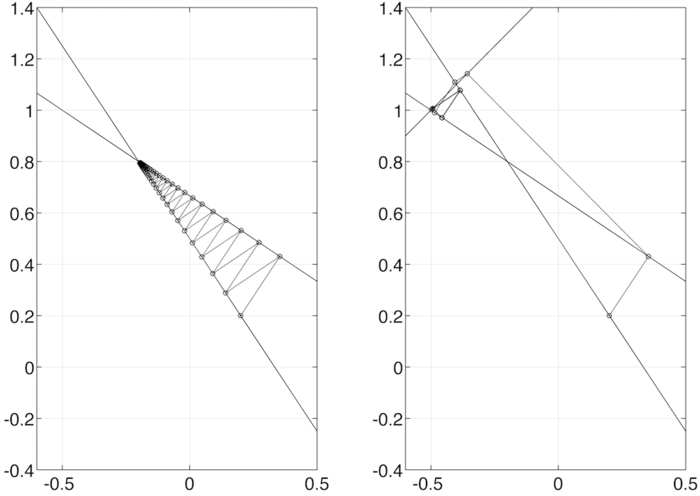
где [math]k[/math] - номер итерации, [math]u^{0}[/math] - начальное приближение, а [math]\lambda_{k} \in \left(0,2\right)[/math] - параметр релаксации (Рисунки 1 и 2 построены для случая, когда [math]\lambda_{k}=1,\,\forall k[/math]).

1.3.2 Геометрическая интерпретация

Метод алгебраической реконструкции достаточно просто формулируется с использованием его геометрической интерпретации. Рассмотрим совместную с.л.а.у. с двумя неизвестными 

[math]A=\begin{pmatrix}3 & 2\\
2 & 3
\end{pmatrix},\text{ }f=\begin{pmatrix}1\\
2
\end{pmatrix}[/math]

и несовместную переопределенную, полученную добавлением к этой системе дополнительного уравнения [math]-u_{1}+u_{2}=1.5[/math]. Каждое уравнение из с.л.а.у. можно интерпретировать как гиперплоскость в пространстве координат, а решение совместной с.л.а.у. - как точку пересечения всех этих гиперплоскостей. При использовании метода алгебраической реконструкции для решения с.л.а.у. поиск приближенного решения осуществляется в направлениях, перпендикулярных к гиперплоскостям, каждая из которых описывается отдельным уравнением решаемой системы (см. Рис.1).

Рисунок 1. К геометрической интерпретации метода алгебраической реконструкции: слева - случай совместной с.л.а.у., справа - несовместной с.л.а.у.

Интерактивная диаграмма для совместного случая подготовлена авторами статьи здесь (Notes about S. Kaczmarz algorithm - consistent case), а для несовместного случая здесь (Notes about S. Kaczmarz algorithm - inconsistent case). Данные диаграммы позволяют регулировать параметры с.л.а.у. и начальное приближение, что позволяет наглядно демонстрировать сходимость итерационной последовательности.

Описанные результаты наводят на очевидную идею - проекционная последовательность влияет на скорость сходимости метода ортогональных проекций. Обратите внимание на Рис.2.

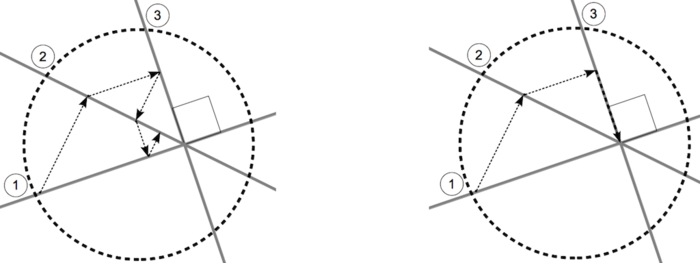
Рисунок 2. Выбор последовательности проектирования в алгоритме С. Качмажа: К выбору последовательности ортогональных проекций: слева - последовательность проектирования начинается от первого к последнему уравнению и в обратном порядке - от последнего к предпоследнему (symART[16][17][18]), а справа - последовательность строится циклическим способом (от последнего к первому уравнению и т.д.)

Как показано на Рис. 2 - итерационная последовательность, в случае Рис. 2 (справа) сходится вообще за конечное число итераций.

1.4 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма Качмажа состоит из двух частей:

  • предварительный расчет норм всех строк матрицы и задание начального приближения к решению,
  • серия итераций на каждой из которых приближенное решение пересчитывается с использованием одной операций SAXPY (scalar multiplication and vector addition) [19] и одного скалярного произведения векторов.

Часть предварительного расчета необходима для оптимизации вычислений внутри итерационного процесса, для этого требуется выделение дополнительной памяти ([math]m[/math] числовых ячеек памяти) для хранения норм строк матрицы.

Расчет очередного приближения решения с.л.а.у. и оценки точности его вычисления выполняются в цикле вплоть до выхода по одному из условий:

  1. достижение необходимой точности;
  2. достижение максимального числа итераций.

Для расчета очередного приближения к решению используются такие макрооперации, как скалярное произведение, умножением вектора на число и сложение векторов.

Оценку сходимости последовательности можно проводить, например, по невязке (на что будут потрачены дополнительные вычислительные ресурсы) или контролируя норму разности приближенных решений между итерациями. Количество сложений, умножений и сравнений прямо пропорционально количеству итераций.

1.5 Макроструктура алгоритма

Опуская предварительный расчет, базовой макрооперацией алгоритма является операция SAXPY. Параллелизация алгоритма ограничена его итерационной природой, а эффективность параллельных реализаций операции SAXPY и скалярного произведения увеличивается с увеличением размерности задачи (фактически, с увеличением количества неизвестных в с.л.а.у. [math]n[/math]). Это особенно важно в задачах обработки изображений.

1.6 Схема реализации последовательного алгоритма

  1. Инициализируем вектор решения первым приближением: [math]u = u^{0}[/math]. В качестве первого приближения зачастую используется нулевой вектор.
  2. Рассчитываем нормы строк матрицы с.л.а.у.: [math]{\Vert A \Vert}[/math].
  3. Вычисляем очередной номер проекции: [math]j\left(k\right)=\left(k\ \bmod\ m\right)+1,\, k=\overline{0,\infty}[/math].
  4. Для целей обеспечения устойчивости, проверяем, что норма соответствующей проекции не близка к нулю и продолжаем вычисления, иначе переходим к новой итерации (пункт 3).
  5. Запоминаем предыдущее приближение решения и вычисляем новое: [math]u^{k+1}=u^{k}+\lambda_{k}\frac{f_{j\left(k\right)}-\left(a_{j\left(k\right)},u^{k}\right)}{\Vert a_{j\left(k\right)}\Vert^{2}}a_{j\left(k\right)}[/math].
  6. Если решение вычислено с заданной точностью, то выходим из цикла; иначе переходим к новой итерации (пункт 3).

1.7 Последовательная сложность алгоритма

Вычислительная сложность алгоритма Качмажа определяется сложностью реализации операции SAXPY - [math]O(n)[/math]. Затраты на предварительный расчет обычно не включают в сложность самого алгоритма. В итоге, общая сложность алгоритма Качмажа зависит от количества итераций и равна [math]k \cdot O(n)[/math], где [math]n[/math] - количество неизвестных в с.л.а.у. При этом, в определенных случаях, можно сделать верхние оценки необходимого количества итераций для нахождения приближенного решения с заданной точностью.

К важным особенностям необходимо отнести, что алгоритмическая сложность каждой итерации не зависит от ее номера, а общий объем памяти, необходимый для реализации алгоритма, линейно зависит от [math]n[/math], но не от [math]m[/math].

1.8 Информационный граф

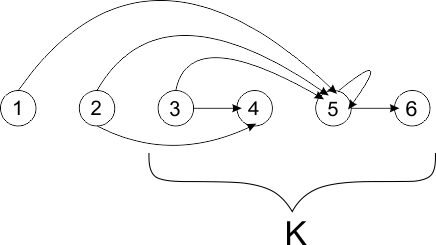
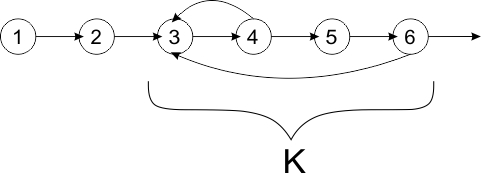
Исходя из описания алгоритма можно построить информационный и операционные графы алгоритма (см. Рис. 3 и 4). В качестве вершин графа выступают этапы последовательного алгоритма (см. пункт 1.6). Графы алгоритма являются параметризованными (зависят от входных данных) и недетерминированными (в смысле, что количество вычислений зависит от начальных данных).

Рисунок 3. Информационный граф алгоритма Качмажа.
Рисунок 4. Операционный граф алгоритма Качмажа.

Из приведенных графов следует, что зависимость каждой итерации цикла от предыдущей исключает параллельную реализацию алгоритма. Фактически, в качестве подготовительных действий возможно одновременно рассчитать начальное приближение, нормы строк матрицы и порядок обхода (номера проекций), остальная часть алгоритма выполняется исключительно последовательно.

1.9 Ресурс параллелизма алгоритма

Алгоритм Качмажа, как любой итерационный алгоритм, является последовательным и в строковой версии алгоритма ресурс для параллелизма оказывается небольшим - только за счет параллельных реализаций операции SAXPY и скалярного произведения.

Однако, существуют различные блочные версии алгоритма Качмажа, где проектирование осуществляется не на конкретную гиперплоскость, а на их пересечение в рамках выбранного блока. Такие модификации имеют существенно больший ресурс для распараллеливания и связаны с трудоемкими задачами псевдообращения и задачей выбора оптимального размера блока (в общем случае не предполагается, что с.л.а.у. разбивается на блоки равных размеров, что еще больше усложняет задачу).

1.10 Входные и выходные данные алгоритма

Входными данными алгоритма являются:

  1. матрица с.л.а.у. [math]A\in R^{m\times n}[/math],
  2. вектор правых частей [math]f\in R^{m}[/math],
  3. требуемая точность [math]\epsilon\gt 0[/math],
  4. а так же максимальное количество итераций [math]K_{max}\in N[/math].

Объем входных данных составляет [math]m \cdot n + m + 2[/math] ячеек памяти.

Выходными данными алгоритма является вектор решения с.л.а.у. [math]u\in R^{n}[/math]. Объем выходных данных составляет [math]n[/math] ячеек памяти.

Важно отметить, что для начала итераций (в случае, когда этап предварительных расчетов опускается) вся с.л.а.у. не нужна, достаточно всего одного уравнения, остальные можно подавать в "решатель" последовательно. Таким образом, в задачах обработки результатов измерений нет необходимости запоминать в оперативной памяти все результаты измерений, достаточно результаты каждого измерения подавать в "решатель" и по завершению итерации - забывать их (особенно интересно, в случае, когда провести измерение повторно оказывается дешевле, чем сохранить его результаты). Как считают авторы, данный факт играл решающую роль в выборе алгоритма для решения задач компьютерной томографии, в которых измерения (срезы синограммы) появляются последовательно, а повторение измерения лишь увеличивает лучевую нагрузку на сканируемый объект и само время сканирования (но, объем лучевой нагрузки, естественно, является критичным для биологических объектов).

1.11 Свойства алгоритма

Вычислительную мощность алгоритма подсчитать затруднительно, так как формально, последовательность приближений сходится к точному решению в пределе.

Вопрос о вычислительной устойчивости алгоритма остается открытым, для уменьшения артефактов вычислений в арифметике с плавающей точкой рекомендуется не использовать в проекционной последовательности те строки матрицы, нормы которых близки к нулю.

Алгоритм недетерминирован по структуре вычислительного процесса: число итераций, а значит и число операций, зависят от входных данных. С другой стороны, алгоритм детерминирован в том смысле, что выдаёт всегда одинаковый результат при одинаковых входных данных (естественно, исключая рандомизированные модификации алгоритма Качмажа).

2 ЧАСТЬ. Программная реализация алгоритма

Ниже представлен прототип программной реализации алгоритма на языке MatLab. Большое количество вариантов реализации и различных модификаций представлено в этих пакетах [20][21]. 

function [ u ] = ART(A, f, maxit, tol)
%ART1 - алгоритм алгебраической реконструкции (С. Качмажа) с циклическим обходом
%   A, f - исходные данные задачи
%   tol - чувствительность правила останова
	[m,n] = size(A); u = zeros(n,1);
	% Нормы строк матрицы с.л.а.у. рассчитываются заранее
	nrma2 = full(abs(sum(A.*A',1)));
	for k = 1:1:maxit     
		j = mod(k-1,m) + 1;
		if (nrma2(j) <= 0), continue, end;
		u_prev = u;
		u = u + (f(j) - (A(j,:)*u))/nrma2(j) * A(j,:)';
		if (norm(u_prev-u) <= tol), break, end;
	end;
end;

2.1 Особенности реализации последовательного алгоритма

В качестве критерия завершения итераций используют наиболее популярные правила останова (но не всегда эффективные): критерий останова по невязке [math]\left\Vert A\cdot u_{k}-f\right\Vert \lt \epsilon[/math] или [math]\left\Vert u_{k-1}-u_{k}\right\Vert \lt \epsilon[/math] (как в представленной реализации). Последний критерий может слишком рано завершать итерации, в виду того, что часто, алгоритм имеет медленную скорость сходимости.

2.2 Локальность данных и вычислений

Алгоритм Качмажа характеризуется высокой пространственной и временной локальностью, которые обуславливаются использованием внутри алгоритма векторных операций (например операции SAXPY).

Важно, при реализации учитывать структуру хранения двумерных массивов в оперативной памяти для выбранной архитектуры. К примеру в языках С/С++, двумерный массив (матрица) из трех строк и четырех колонок будет сохранен в памяти в следующей последовательности: (1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4) - элементы матрицы выписываются последовательно, по строкам.

Однако, при реализации на языке FORTRAN эта же матрица будет сохранена в следующей последовательности: (1,1),(2,1),(3,1),(1,2),(2,2),(3,2),(1,3),(2,3),(3,3),(1,4),(2,4),(3,4) - элементы матрицы выписываются последовательно, по столбцам [22]. При реализации на FORTRAN подобных языках, матрицу [math]A[/math] из входных данных следует хранить в оперативной памяти в транспонированном виде, таким образом существенно возрастает пространственная локальность векторных операций, в которых участвуют строки матрицы с.л.а.у.

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

Как было сказано выше, ресурсом параллелизма в алгоритме являются векторные операции: SAXPY и скалярное произведение векторов. Данные макрооперации имеют высокую степень параллелизма и могут быть реализованы для различных классов архитектур. Однако факт того, что вычисления выполнятюся многократно в цикле, требующем полного вектора решения на этапе проверки достижения необходимой точности, говорит о целесообразности применения архитектур с общей памятью.

Так же стоит отметить что графические процессоры хорошо зарекомендовали себя для реализации матричных и векторных операций, в частности той же операции SAXPY, например, в [23].

2.7 Существующие реализации алгоритма

Множество модификаций алгоритма Качмажа реализовано в следующих расширениях для математического пакетата MatLab:

  • Hansen, P. C. AIR Tools – A MATLAB package of algebraic iterative reconstruction methods [20]
  • Hansen, P. C. Regularization Tools: A MATLAB package for Analysis and Solution of Discrete Ill-Posed Problems. Version 4.1. [24]
  • Ivanov, A. A. Regularization Kaczmarz Tools Version 1.4 for Matlab, Matlabcentral Fileexchange [21].

3 ЧАСТЬ. Дополнительная информация

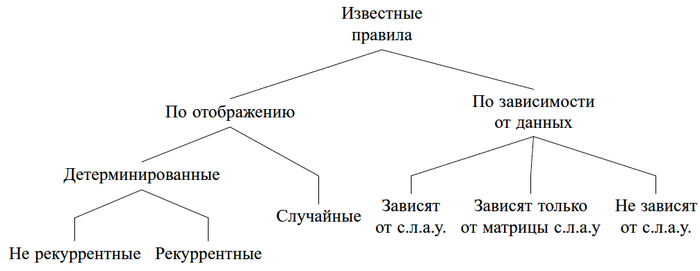
3.1 Классификация проекционных последовательностей

Под проекционной последовательностью понимается порядок обхода уравнений системы в процессе итераций алгоритма Качмажа. А рассматриваемая последовательность задается с использованием правила [math]j\left(k\right)[/math], где [math]k\in N_{0}[/math] которое позволяет вычислить номер используемого уравнения на итерации с номером [math]k[/math]. Правило [math]j\left(k\right)[/math]рассматривать как сюръективное отображение множества [math]N_{0}[/math] на множество [math]\left\{ 1,2,\ldots,m\right\}[/math], где [math]m[/math] - количество уравнений в с.л.а.у. [math]Au=f,\ A\in R^{m\times n},\ u\in R^{n},\ f\in R^{m}[/math].

Отображения такого вида могут быть как детерминированными, так и случайными, рандомизированными. В последнем случае [math]j\left(k\right)[/math] является дискретной случайной величиной с заданным законом распределения. Например, к детерминированным отображениям необходимо отнести:

  • правило циклического обхода [math]j\left(k\right)=\left(k\ \bmod\ m\right)+1,\, k=\overline{0,\infty}[/math];
  • метод четной перестановки - эвристический метод для задач компьютерной томограции из [25];
  • симметричное правило (symmetric ART), в котором последовательность проектирования на гиперплоскости идет в начале в прямом порядке от первого уравнения к последнему, а затем в обратном порядке - от последнего - к первому.

Существенно важной является классификация рассматриваемых правил по их зависимости от данных. Например, результат из [13], где [math]j\left(k\right)[/math] является дискретной случайной величиной с заданным законом распределения [math]P\left(j\left(k\right)=i\right)=\frac{\left\Vert a_{i}\right\Vert _{2}^{2}}{\left\Vert A\right\Vert _{F}^{2}}[/math], где [math]\left\Vert \cdot\right\Vert _{F}[/math] - матричная норма Фробениуса и [math]\left\Vert a_{i}\right\Vert[/math] - евклидова норма строки матрицы с.л.а.у. с номером [math]i=\overline{1,m}[/math]. Этот результат качественно отличается от всех известных рандомизированных способов наличием зависимости от матрицы с.л.а.у - от исходных данных задачи.

Рисунок 3. Классификация правил для задания проекционной последовательности в алгоритме C. Качмажа

3.2 Рандомизированная версия алгоритма и скорость сходимости

При решении с.л.а.у. сверхбольшой размерности использование всех уравнений системы может оказаться избыточным, более того, учесть все уравнения системы, полученные в результате некоторых измерений, может не быть технической возможности, что обусловлено ограниченными ресурсами ЭВМ. Существуют подходы, связанные с обработкой данных решаемой задачи, цель которых состоит в отборе только информативных результатов измерений.

Например, при решении задачи идентификации оптических искажающих систем [26] следует использовать не весь объем измерений, а только тот, что выполнен для в определенном смысле информативных фрагментов изображений. Формально это соответствует удалению части уравнений из с.л.а.у., которые оказываются линейно зависимыми и отрицательным образом влияют на обусловленность задачи [27], что, в свою очередь, приводит к крайне медленной скорости сходимости известных итерационных алгоритмов.

Таким образом, основная цель рандомизации итерационных проекционных алгоритмов решения с.л.а.у. состоит в том, чтобы обеспечить скорость сходимости (а значит и вычислительную сложность), независимую от количества уравнений в системе (количества измерений) [28], но при решении не использовать систему целиком, а только отдельные уравнения, выбранные определенным случайным образом.

Наиболее простым и очевидным способом случайную последовательность [math]j\left(k\right)[/math] определяют с использованием дискретного равномерного закона распределения [math]P\left(j\left(k\right)=i\right)=\frac{1}{m}[/math].

Таким образом, в процессе итераций все уравнения системы будут участвовать в решении задачи примерно одинаковое число раз. Данный способ задания [math]j\left(k\right)[/math] обширно используют в работах [13] [29], посвященных рандомизации итерационных алгоритмов, в качестве базового, для демонстрации преимущества новых подходов. В указанных работах, их авторы произвели настоящую революцию в рандомизации алгоритма Качмажа, указав закон распределения, определяющий последовательность [math]j\left(k\right)[/math] таким образом, что итерационная последовательность имеет экспоненциальную скорость сходимости. Их результат формулируется в виде следующей важной теоремы:

Пусть [math]Au=f\ A\in R^{m\times n},\ u\in R^{n},\ f\in R^{m}[/math] - совместная переопределенная \left(m\geq n\right) с.л.а.у., а [math]u_{0}[/math] - некоторое начальное приближение к ее решению, и для рекуррентной формулы алгоритма Качмажа значения последовательности [math]j\left(k\right)[/math] определяются с использованием закона распределения: [math] P\left(j\left(k\right)=i\right)=\frac{\left\Vert a_{i}\right\Vert _{2}^{2}}{\left\Vert A\right\Vert _{F}^{2}}, [/math] где [math]\left\Vert \cdot\right\Vert _{F}[/math] - матричная норма Фробениуса.

Тогда последовательность приближенных решений в алгоритме Качмажа сходится к решению с.л.а.у. со средней ошибкой, которая на каждой итерации оценивается с использованием неравенств

[math] M\left[\left\Vert u^{k}-u^{*}\right\Vert _{2}^{2}\right]\leq\left(1-\kappa\left(A\right)^{-2}\right)^{k}\left\Vert x^{0}-x^{*}\right\Vert _{2}^{2}, [/math]

[math] \left(1-2k\cdot\kappa\left(A\right)^{-2}\right)\left\Vert x^{0}-x^{*}\right\Vert _{2}\leq M\left[\left\Vert u^{k}-u^{*}\right\Vert _{2}\right]. [/math]

В приведенных неравенствах величина [math]\kappa\left(A\right)=\left\Vert A\right\Vert _{F}\left\Vert A^{+}\right\Vert _{2}[/math] является одной из оценок [math]1\leq\frac{\kappa\left(A\right)}{\sqrt{n}}\leq k\left(A\right)[/math] спектрального числа обусловленности матрицы с.л.а.у. [math]k\left(A\right)=\left\Vert A\right\Vert _{2}\left\Vert A^{+}\right\Vert _{2}[/math], предложенной в [30] (здесь [math]A^{+}[/math] - псевдообратная матрица, в то же время левая обратная матрица для [math]A[/math]).

До публикации работ Штромера (Strohmer, T.) не существовало оценок скорости сходимости алгоритма Качмажа в терминах числа обусловленности матрицы с.л.а.у. Данная теорема также наиболее точно демонстрирует цель рандомизации - показать, что скорость сходимости не зависит от [math]m[/math] - количества уравнений в системе, но зависит от порядка системы [math]n[/math].

3.3 Алгоритм Качмажа как метод максимального уменьшения ошибки на каждой итерации

3.4 Алгоритм Качмажа с четной перестановкой

Данная эвристика оказывается, пожалуй, одной из самых изящных и определяет отображение [math]j\left(k\right)[/math] следующим образом. В работе [31] предлагается алгоритм MLS (multilevel scheme) для переупорядочивания строк в матрице таким образом, чтобы каждое следующее проецирование в итерационной последовательности осуществлялось на гиперплоскость, наиболее ортогональную к текущей (только для матриц в задачах томографии). Допустим, что имеется 8 проекций (в матрице с.л.а.у. - всего восемь строк), снятых под углами в 0, 22.5, 45 ,67.5, 90, 112.5, 135 и 157.5 градусов, тогда период последовательности [math]j\left(k\right)[/math] выглядит как: [math]{0,4,2,6,1,5,3,7}[/math].

Когда количество проекций (строк в с.л.а.у.) является степенью двойки, то [math]j\left(k\right)[/math] совпадет с последовательностью, которая используется для реализации алгоритма «на месте» одномерного быстрого преобразования Фурье, например в [32].

Формально, данная модификация эквивалентна исходному алгоритму с циклическим правилом обхода, который применяется к с.л.а.у. [math]D \cdot A \cdot u=D \cdot f[/math] , где [math]D\in R^{m\times m}[/math] суть - перестановочная матрица.

В чем же состоит изящность данного способа задания отображения [math]j\left(k\right)[/math]? Правило четной перестановки, было специально разработано для решения задачи восстановления данных по измерениям, выполненным с использованием компьютерного томографа с параллельной схемой сканирования. Правило построено его авторами из интуитивных соображений о структуре самих данных, а не их значений.

4 Литература

  1. ↑ Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М.: Лаборатория Базовых Знаний, 2000.
  2. ↑ Natterer, Frank (2001), "V.3 Kaczmarz's method", The Mathematics of Computerized Tomography, Classics in Applied Mathematics 32, SIAM, p. 128, ISBN 9780898714937.
  3. ↑ Kaczmarz, S. Angenäherte Auflösung von Systemen linearer Gleichungen [Текст] / S. Kaczmarz // Bulletin International de l'Académie Polonaise des Sciences et des Lettres / Classe des Sciences Mathématiques et Naturelles. Série A, Sciences Mathématiques. — 1937. — Vol. 35. — С. 355-357.
  4. ↑ Hounsfield, G. N. A Discussion on Recent Developments in Medical Endoscopy and Related Fields [Текст] / G. N. Hounsfield // Proceedings of the Royal Society of London. Series B, Biological Sciences. — 1977. — Vol. 195, N. 1119. — С. 281-289.
  5. ↑ Gordon, R. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography [Текст] / R. Gordon, R. Bender, G. T. Herman // Journal of theoretical biology. — 1970. — Vol. 29, Issue 3. — С. 471–481.
  6. ↑ Micke, A. The Mathematics of Computerized Tomography [Текст] / A. Micke, F. Natterer // ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik (Journal of Applied Mathematics and Mechanics). — 1987. — Vol. 67, Issue 11. — С. 580. —ISBN 3-519-02103-X and 0-471-90959-9.
  7. ↑ Herman, G. T. Fundamentals of computerized tomography: Image reconstruction from projection [Текст] : 2nd ed. / G. T. Herman. — Springer, 2009. — 300 с.
  8. ↑ Sezan, K. M. Applications of convex projection theory to image recovery in tomography and related areas [Текст] / K. M. Sezan, H. Stark // Image Recovery: Theory and Application / H. Stark, editor. — Academic Press, 1987. — С. 415-462.
  9. ↑ Cegielski, A. Bibliography on the Kaczmarz method [Электронный ресурс] : Faculty of Mathematics, Computer Science and Econometrics University of Zielona Gora ; Poland, March, 28th, 2010 / Режим доступа: http://www.uz.zgora.pl/~acegiels/Publikacje-Kaczmarz.pdf
  10. ↑ Ильин, В. П. Об итерационном методе Качмажа и его обобщениях [Текст] / В. П. Ильин // Сибирский журнал индустриальной математики. — 2006. — Т. 9, вып. 3. — С. 39–49.
  11. ↑ Г. П. Васильченко, А. А. Светлаков, “Проекционный алгоритм решения систем линейных алгебраических уравнений большой размерности”, Ж. вычисл. матем. и матем. физ., 20:1 (1980), 3–10.
  12. ↑ Л. Г. Гурин, Б. Т. Поляк, Э. В. Райк, “Методы проекций для отыскания общей точки выпуклых множеств”, Ж. вычисл. матем. и матем. физ., 7:6 (1967), 1211–1228
  13. ↑ 13,0 13,1 13,2 Strohmer, T. A Randomized Kaczmarz Algorithm with Exponential Convergence [Текст] / T. Strohmer, R. Vershynin // Journal of Fourier Analysis and Applications. — 2009. — Vol. 15, Issue 2. — С. 262-278.
  14. ↑ Marks, L. D. A feasible set approach to the crystallographic phase problem [Текст] / L. D. Marks, W. Sinkler, E. Landree // Acta Crystallographica Section A. — 1987. — Vol. 55, Issue 4. — С. 601-612.
  15. ↑ JElble, J. M. GPU computing with Kaczmarz’s and other iterative algorithms for linear systems [Текст] / J. M. Elble, N. V. Sahinidis, P. Vouzis // Parallel Computing. — 2010. — Vol. 36, Issues 5-6. — С. 215–231.
  16. ↑ Bjorck, A. Accelerated projection methods for computing pseudoinverse solutions of systems of linear equations [Текст] / A. Bjorck, T. Elfving // BIT Numerical Mathematics. — 1979. — Vol. 19, Issue 2. — С.145-163.
  17. ↑ Nikazad, T. Algebraic Reconstruction Methods [Текст] : PhD. Thesis, Linköping University / T. Nikazad. — Linköping, 2008.
  18. ↑ Kamath, G. Component-Average Based Distributed Seismic Tomography in Sensor Networks [Текст] / G. Kamath, L. Shi, W.-Z. Song // IEEE International Conference on Distributed Computing in Sensor Systems. — 2013. — С. 88-95.
  19. ↑ Mark Harris. Six Ways to SAXPY https://devblogs.nvidia.com/parallelforall/six-ways-saxpy/
  20. ↑ 20,0 20,1 Hansen, P. C. AIR Tools – A MATLAB package of algebraic iterative reconstruction methods [Электронный ресурс] / Режим доступа: http://www2.compute.dtu.dk/~pcha/AIRtools/
  21. ↑ 21,0 21,1 Ivanov, A. A. Regularization Kaczmarz Tools Version 1.4 for Matlab, Matlabcentral Fileexchange [Электронный ресурс] / Режим доступа: http://www.mathworks.com/matlabcentral/fileexchange/43791
  22. ↑ How FORTRAN Stores Two-Dimensional Arrays in Memory, https://support.microsoft.com/en-us/kb/27780
  23. ↑ А.Ю. Суравикин, В.В. Коробицын Оценка производительности связывания CUDA с графическим API на примере задачи SAXPY / Математические структуры и моделирование. - 2010ю - Т.21. - С. 96-103.
  24. ↑ Hansen, P. C. Regularization Tools: A MATLAB package for Analysis and Solution of Discrete Ill-Posed Problems. Version 4.1., http://www2.compute.dtu.dk/~pcha/Regutools/
  25. ↑ Guan H. A projection access order for speedy convergence of ART (algebraic reconstruction technique): a multilevel scheme for computed tomography [Текст] / Guan H., R. Gordon // Physics in Medicine and Biology. — 1994. — Vol. 39, N. 11. — С. 2005-2022.
  26. ↑ Фурсов, В.А. Идентификация оптических искажающих систем с отбором информативных фрагментов изображений [Текст] / В.А. Фурсов // Компьютерная оптика. — 1995. —Вып. 15, ч.1. — С. 79–89.
  27. ↑ Фурсов, В.А. Введение в идентификацию по малому числу наблюдений. [Текст] / В.А. Фурсов. — М. : Изд-во МАИ, 1991. —36 с.
  28. ↑ Sabelfeld, K Stochastic iterative projection methods for large linear systems [Текст] / K. Sabelfeld, N. Loshchina // Monte Carlo Methods and Applications. — 2010. — Vol. 16, Issue 3-4. — С. 343-359.
  29. ↑ Strohmer, T. A randomized solver for linear systems with exponential convergence [Текст] / T. Strohmer, R. Vershynin // Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. — Springer; 2006. С. 499-507.
  30. ↑ Demmel, J. The probability that a numerical analysis problem is difficult [Текст] / J. Demmel // Mathematics of Computation. . — 1988. — Vol. 50, Issue 182. — С. 449–480.
  31. ↑ Guan H. A projection access order for speedy convergence of ART (algebraic reconstruction technique): a multilevel scheme for computed tomography [Текст] / Guan H., R. Gordon // Physics in Medicine and Biology. — 1994. — Vol. 39, N. 11. — С. 2005-2022.
  32. ↑ Cooley, J.W. An algorithm for the machine calculation of complex Fourier series [Текст] / J.W. Cooley, J. W. Tukey // Mathematics of Computation. — 1965. — Vol. 19, N. 90. — С. 297–301.
Источник — https://algowiki-project.org/w/ru/index.php?title=Алгоритм_Качмажа&oldid=3958