Метод Гаусса решения СЛАУ (прямой ход)

2 Программная реализация

2.2 Описание локальности данных и вычислений

2.2.2 Описание локальности реализации алгоритма

2.2.2.1 Описание структуры обращений в память и качественная оценка локальности

Рисунок 12.1. Прямой ход метода Гаусса решения СЛАУ. Общий профиль обращений в память

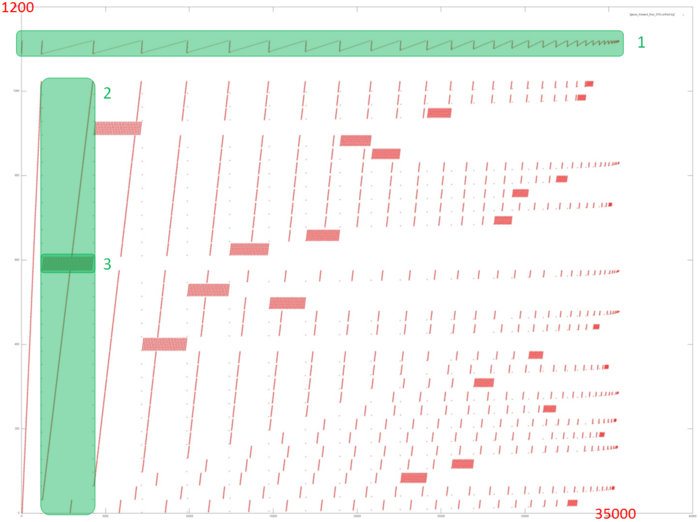
На рисунке 12.1 представлен профиль обращений в память для прямого хода метода Гаусса решения СЛАУ. Из исходного кода, как и из рисунка, видно, что в программе задействовано 2 основных массива: профиль обращений к элементам первого выделен зеленым (фрагмент 1); все остальные обращения происходят к элементам второго массива. Видно, что общий профиль всей программы устроен достаточно сложно. Основное, что можно заметить из данного рисунка, – это итерационная природа профиля, причем каждая следующая итерация содержит меньше обращений. Это особенно хорошо видно по фрагменту 1.

Далее, как известно, в прямом ходе Гаусса на каждой итерации отбрасывается из рассмотрения одна из строк СЛАУ. Это отчетливо видно и на рис. 12.1: на каждой итерации (одна из них выделена как фрагмент 2) выполняется серия обращений, связанных с отбрасываемой строкой (фрагмент 3), после чего обращения к этим элементам больше не выполняются. Также можно заметить, что фрагменты, подобные фрагменту 3, на каждой последующей итерации становятся все меньше, как по числу обращений, так и по числу элементов, к которым происходят обращения.

Однако на основе подобной общей картины очень сложно дать даже качественные оценки локальности. Перейдем к более подробному рассмотрению фрагмента 1, соответствующего обращениям к одному из двух массивов.

Рисунок 12.2. Фрагмент 1 (профиль обращений к первому массиву)

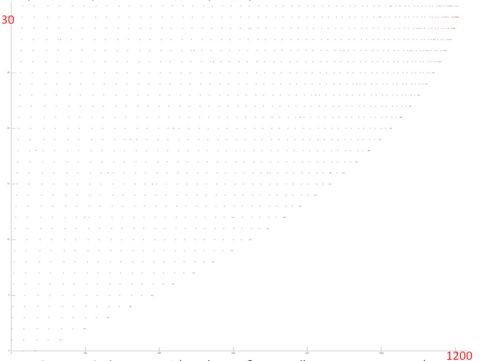
На рис. 12.2 показан отдельно фрагмент 1, выделенный на рис. 12.1 зеленым. Наблюдается довольно интересная картина: исходя из рис. 12.1, складывалось впечатление, что данный профиль образуется чередованием итераций двух разных циклов, причем итерация первого цикла заметно короче итераций второго цикла. На самом же деле, из рис. 12.2 можно увидеть, что профиль состоит из однотипных итераций, в рамках которых производится последовательный перебор элементов массива. При этом на каждой следующей итерации отбрасывается элемент с минимальным индексом. Иллюзия наличия двух разных циклов обусловлена исключительно числом обращений к другому массиву – когда число таких обращений велико, итерация данного фрагмента кажется длиннее. При этом во фрагменте 1 (как видно на рис. 12.2) число обращений всего лишь около 1200, тогда как весь профиль обращений состоит из 34 тысяч. То есть на долю обращений к первому массиву приходится всего 3.5% всех обращений в программе.

Поскольку основа данного профиля – последовательный перебор элементов массива, можно сказать, что данный фрагмент обладает высокой пространственной локальностью. А поскольку итераций с перебором элементов достаточно много, также видно, что и временна́я локальность достаточно высока.

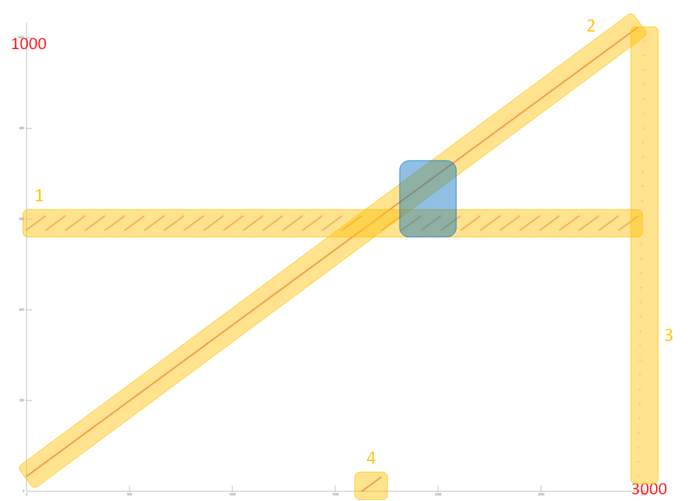
Теперь перейдем к рассмотрению профиля обращений ко второму массиву, который значительно больше и сложнее первого профиля. На рис. 12.3 отдельно представлен фрагмент 2, выделенный на рис. 12.1. Такой фрагмент устроен из четырех частей, отмеченных на рисунке оранжевым.

Рисунок 12.3. Фрагмент 2 (итерация профиля обращений ко второму массиву)

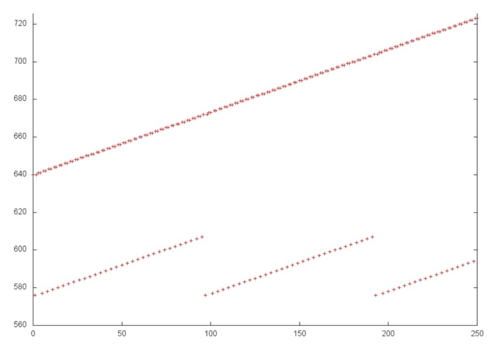
Часть 1 очень похожа на повторяющийся последовательный перебор одного и того же небольшого числа элементов в цикле. При более близком рассмотрении можно убедиться, что это действительно так. На рис. 12.4 показано приближение фрагмента 2, выделенное на рис. 12.3 синим цветом. Также на этом рисунке видно, что часть 2 представляет собой практически полное подобие последовательного перебора всех элементов данного массива. Таким образом, обе эти части обладают высокой пространственной локальностью (из-за последовательного перебора). При этом часть 1 обладает также высокой временной локальностью, поскольку перебор повторяется в цикле, в отличие от части 2, где к каждому элементу выполняется только одно обращение.

Часть 3 состоит всего из нескольких обращений и представляет собой перебор всех элементов массива, выполненных с достаточно большим шагом, гораздо большим, чем в части 2. В данном случае, из-за достаточно большого шага, наблюдается невысокая пространственная локальность и отсутствие временно́й локальности, так как перебор выполняется единожды.

Часть 4 представляет собой последовательный перебор части массива, по размеру соответствующей числу отброшенных из рассмотрения элементов; чем ближе к концу профиля, тем больше обращений расположено в части 4. Эта часть обладает теми же свойствами локальности, что и часть 2. Отличие заключается в числе обращений, однако в данном случае это не оказывает сильное влияние на локальность.

При рассмотрении фрагмента 2 в целом основное влияние оказывают части 1 и 2, поэтому можно утверждать, что это фрагмент обладает достаточно высокой и пространственной, и временно́й локальностью. Однако на последующих итерациях (см. рис. 12.1) локальность в целом будет постепенно снижаться, поскольку на каждой итерации отбрасывается из рассмотрения некоторая часть элементов.

Рисунок 12.4. Приближение фрагмента 2

2.2.2.2 Количественная оценка локальности

Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

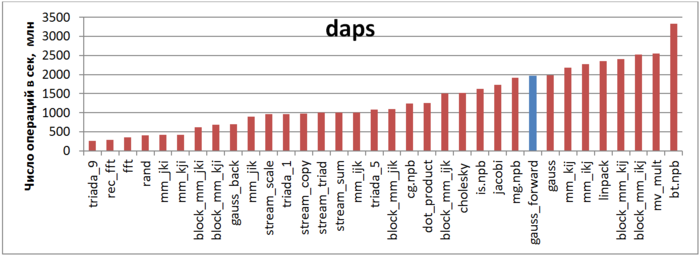
На рисунке 12.5 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что отмеченный синий столбец, соответствующий прямому ходу метода Гаусса, расположен в правой части и показывает достаточно высокую производительность, немного ниже производительности теста Линпак. Также отметим, что значение daps для данной задачи практически совпадает со значением daps для всего метода Гаусса (столбец «gauss»), объединяющего как прямой, так и обратный ход. Это связано с тем, что обратный ход состоит из гораздо меньшего числа обращений, нежели прямой ход, поэтому оказывает меньшее влияние.

Рисунок 12.5. Сравнение значений оценки daps

Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.

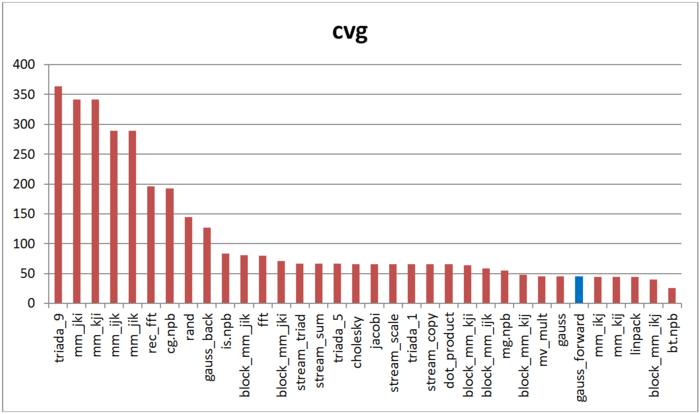
На рисунке 12.6 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, как и в случае с оценкой daps, прямой ход метода Гаусса обладает высокой локальностью. Причем согласно данной оценке тест Линпак показывает практически те же результаты. Отметим, что снова значение оценки для отдельно прямого хода и совокупности прямого и обратного ходов (столбец «gauss») совпадают.

Рисунок 12.6. Сравнение значений оценки cvg

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Описание масштабируемости реализации алгоритма

Рисунок 1. Параллельная реализация Скалярного произведения векторов Максимальная производительность.

Рисунок 2. Параллельная реализация Скалярного произведения векторов Максимальная эффективность.

Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:

• число процессоров [4 : 256]
• размер матрицы [1024 : 5120]

Эффективность выполнения реализации алгоритма

• Минимальная эффективность 0,11 %
• Максимальная эффективность 6.65%

Оценка масштабируемости

• По числу процессов: -0.000101 – при увеличении числа процессов эффективность в целом уменьшается по рассматриваемой области, хотя и менее интенсивно, чем при увеличении числа процессов. Учитывая разницу между максимальным и минимальным значением эффективности в 6,5% можно сделать вывод, что на рассмотренной области снижение эффективности, скорее всего, достаточно равномерное. Снижение эффективности объясняется тем, что при росте вычислительной сложности существенно возрастают объемы передаваемых данных. Могут присутствовать области возрастания эффективности, на всех рассмотренных размерах матрицы. Это может объясняться увеличением вычислительной сложности задачи, что при постоянных накладных расходах на организацию параллельного взаимодействия приводит к общему увеличению эффективности работы.
• По размеру задачи:-0.00674– при увеличении размера задачи эффективность в целом уменьшается по рассматриваемой области. Это может свидетельствовать о том, что при увеличении размера задачи возрастают и накладные расходы на организацию параллельного взаимодействия. Так как интенсивность снижения эффективности по этому направлению выше, чем по направлению числа процессов, скорее всего падение интенсивности значительно при малом числе процессов более интенсивное, чем в присутствующих областях возрастания эффективности при большом числе процессов.
• По двум направлениям: -6.621e-05 – при рассмотрении увеличения, как вычислительной сложности, так и числа процессов по всей рассмотренной области значений уменьшается, однако интенсивность уменьшения эффективности очень мала. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров составляет почти 6,5 % говорит о том, что если на поверхности присутствуют области с очень интенсивным изменением эффективности, но очень малые по площади. На остальной поверхности изменения эффективности незначительны и находятся на приблизительно одном и том же уровне.