Участник:Kanast74/Алгоритм кластеризации, основанный на минимальном покрывающем дереве

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация - это задача статистического анализа, состоящая в разбиении множества объектов на группы, называемые кластерами, внутри которых объекты обладают одними и теми же свойствами (чаще всего, это означает близость относительно заданной метрики). Основное отличие от задачи классификации состоит в том, что группы заранее не заданы и определяются в процессе работы алгоритма. Необходимость кластеризовать объекты может возникнуть в любой сфере анализа данных, например, при разделении веб-документов на жанры, а также в задачах распознавания образов и анализа социальных сетей.

Таким образом, на начальном этапе решения задачи имеются набор тестовых примеров [math]X=\{x_1...x_n\}[/math], а также функция расстояния между ними [math]w(e)[/math]. При этом метрика выбирается исходя из требований задачи, но наиболее распространенные - это Евклидово расстояние, квадрат Евклидова расстояния, манхэттенская метрика, расстояние Чебышева и степенное расстояние. Далее необходимо применить один из алгоритмов кластеризации, которые можно разделить на две категории: иерархические, состоящие в последовательном поиске кластеров из уже найденных кластеров, а также неирархические, цель которых состоит в минимизации некоторой целевой функции. К последней группе относятся такие алгоритмы, как алгоритм k-средних, алгоритм EM, нечеткие алгоритмы, а также алгоритмы теории графов, к категории которых относится алгоритм, описываемый в данной статье.

Рассмотрим алгоритм кластеризации на k кластеров, основанный на построении минимального остовного дерева (MST) состоит в следующем:

1. По исходным данным строится взвешенный неориентированный граф: каждый объект представляется в виде вершины графа, а вес ребра, связывающего две вершины, есть расстояние между объектами в выбранной заранее метрике
2. Для полученного графа строится минимальное остовное дерево, то есть дерево, содержащее все вершины графа и имеющее минимальный суммарный вес своих ребер
3. Удаляется k-1 ребро минимального остовного дерева с максимальным весом
4. Получаются k компонент связности, которые интерпретируются как кластеры

Для построения минимального остовного дерева могут быть использованы различные алгоритмы, среди которых наиболее распространены:

1. Алгоритм Крускала
2. Алгоритм Борувки
3. Алгоритм Прима

Отметим, что в рамках проведенного исследования использовался алгоритм Крускала, наиболее подробно изучить который можно, пройдя по ссылке [Алгоритм Крускала], поэтому в данной статье его описание не приводится.

1.3 Вычислительное ядро алгоритма

Алгоритм Крускала — алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые описан Джозефом Крускалом в 1956 году.

Алгоритм Крускала находит безопасное ребро для добавления в растущий лес путем поиска ребра [math](u, v)[/math] с минимальным весом среди всех ребер, соединяющих два дерева в лесу. Обозначим два дерева, соединяемые ребром [math](u, v) [/math], как [math]C_1[/math] и [math]C_2[/math]. [math](u, v)[/math] — безопасное для [math]C_1[/math] ребро. Алгоритм Крускала является жадным, поскольку на каждом шаге он добавляет к лесу ребро с минимально возможным весом.

1.4 Макроструктура алгоритма

1. Построение графа путем задания списков ребер. В общем случае, когда задано некоторое множество объектов, для построения графа может быть использован алгоритм, позволяющий рассчитать расстояние от каждого объекта до каждого за [math]O(n^2)[/math] операций, где [math]n[/math] число объектов (вообще говоря, данная операция требует [math]O(E)[/math] операций, где [math]E[/math] - число ребер в графе, но в нашем случае число ребер подразумевается равным [math]E=\frac{D (n(n-1))}{2}[/math], [math]D[/math] - плотность графа). Однако в рамках данного исследования для тестирования алгоритма использовалась такая технология построения графов, когда в качестве веса каждого ребра назначается некоторое произвольное число из заданного промежутка (например, от 1 до 1000), что также требует [math]O(n^2)[/math]
2. Построение минимального остовного дерева на основании полученного ранее графа, для чего может быть использован один из известных и наиболее распространенных алгоритмов (алгоритм Крускала, алгоритм Борувки или алгоритм Прима). Рассмотрим, например, алгоритм Крускала. На начальном этапе имеется граф, состоящий из вершин - объектов исходной выборки и не содержащий ребер, следовательно, каждая из вершин изначально представляет собой компоненту связности и даже дерево. Алгоритм состоит в выборе на каждом шаге ребра с минимальным весом и добавлении его в дерево, если оно соединяет два дерева. Алгоритм будет работать максимально эффективно, если изначально ребра графа, полученного на первом шаге будут отсортированы (например, по возрастанию).
3. Наконец, для получения [math]k[/math] необходимо удалить из получившегося минимального остовного дерева [math]k-1[/math] ребро с максимальным весом. В частности, в случае, если на предыдущем шаге мы пользовались алгоритмом Крускала для построения MST, ребра получившегося дерева отсортированы по возрастанию, значит для удаления указанных выше ребер потребуется лишь [math]O(1)[/math] операций

1.4.1 Используемые обозначения и структуры данных

Для построения минимального остовного дерева используются три операции, опишем здесь каждую из них:

1. операция MakeSet([math]v[/math]) генерирует дерево (множество) для вершины графа [math]v[/math], являющейся корнем искомого дерева
2. операция Find([math]v[/math]) определяет, которому из деревьев принадлежит интересующая вершина [math]v[/math]. Условимся, что данная операция возвращает ту вершину, которая является корнем искомого дерева
3. операция Union([math]u, v[/math]) объединяет два множества (два дерева, содержащих соответствующие вершины) под одним корнем

1.5 Схема реализации последовательного алгоритма

Приведем здесь псевдокод основной части алгоритма - а именно построения локального минимального остовного дерева при помощи алгоритма Крускала.

Kruskal ( G=(V,E) ):

1. mst = ∅;

2. сортировать E по возрастанию;

3. для каждой вершины v из множества вершин V:

4. MakeSet(v);

5. для каждого ребра e = (u, v) из множества ребер E:

6. if Find(u) ≠ Find(v):

7. mst = mst ∪ { (u,v) };

8. Union(u, v);

9. return mst;

1.6 Последовательная сложность алгоритма

Сперва оценим последовательную сложность составных частей алгоритма.

0. O(V): Формирование графа

1. O(1): Инициализация пустого множества.

2. O(Elog(E)): сортировка ребер из множества E.

3. O(V): Инициализация одноточечного множества для каждой вершины из V.

4. ▲ MakeSet за O(1).

5. O(Elog(V)): Операции Union и Find для каждого ребра из E.

6. ▲ Find за O(1).

7. ▲ Присоединение элемента за O(1).

8. ▲ Union за O(log(V)).

9. O(1): Удаление k-1 ребра для получения k компонент связности

10. O(1): Return.

Таким образом, с учетом того, что, получаем:

[math]T( G = (V, E) ) = O(1) + O(E\log(E)) + O(V) + O(E\log(V)) = O(E\log(E)) + O(E\log(V)) = O(E\log(V)) + O(E\log(V))[/math]

Итак, оценка сложности алгоритма есть [math]T( G = (V, E) ) = O(E\log(V)) + O(\log(V))[/math]

1.7 Информационный граф

Рисунок 1. Информационный граф алгоритма

1.8 Ресурс параллелизма алгоритма

Описанный алгоритм позволяет произвести распараллеливание, источник которого будет описан в данном пункте. Прежде всего, необходимо отметить, что данный алгоритм допускает преобразование в гибридную параллельную версию, а именно версию с использованием технологий MPI и OpenMP.

Следующее свойство позволяет использовать алгоритм Крускала для организации параллельного или распределённого вычисления минимального остовного дерева.

Ассоциативность по рёбрам. Пусть [math]MSF(E)[/math] – минимальный остовный лес графа с рёбрами [math]E[/math]. Тогда

[math] MSF(E_1 \cup E_2 \cup \dots \cup E_k) = MSF(MSF(E_1) \cup MSF(E_2) \cup \dots \cup MSF(E_k)). [/math]

В том случае, когда все объекты заранее известны, и между ними можно рассчитать все попарные расстояния, первый шаг - построение графа - позволяет произвести распараллеливание при помощи обеих вышеуказанных технологий, а именно: разделить объекты между процессами при помощи MPI, а внутри каждой из полученных групп будем рассчитывать попарные расстояния параллельно на нескольких ядрах, использовав технологию OpenMP. Однако в данном исследовании кластеризуемые объекты предполагались заранее неизвестными, так как попарные расстояния между объектами задаются случайным образом, а это означает, что произвести распараллеливание этого шага, которое бы дало хотя бы небольшое ускорение (уменьшение времени работы), не получится.

Если все же объекты заранее были известны, можно сохранить полученную на предыдущем этапе группировку их на отдельные процессы и внутри каждого произвести сортировку расстояний между объектами по возрастанию при помощи алгоритма QSort с использованием технологии OpenMP (в противном случае параллельная структура алгоритма поддерживается начиная с этого шага).

Далее внутри каждой группы объектов (каждый процесс в отдельности) строим минимальное остовное дерево, в конце шага деревья объединяются в одно - общее MST для всех объектов, поддерживая при этом отсортированность расстояний по возрастанию.

Наконец, будем удалять необходимое количество ребер глобального остовного дерева для того, чтобы получить требуемое количество кластеров - компонент связности графа.

1.8.1 Способы разделения графа

Наивный подход к разделению графа на подграфы, которые будут обрабатываться различными процессами, а именно обычное разделение входных данных на несколько подгрупп может не дать желаемых результатов в увеличении производительности алгоритма, так как, вообще говоря, при вычислении каждого локального минимального остовного дерева будет удалено незначительное количество ребер (например, потому, что многие ребра будут принадлежать различным компонентам связности, что приведет к отсутствию циклов, а значит и отсутствию необходимости удалять какие-либо ребра).

Правильный подход к разделению графа на подграфы состоит в том, чтобы каждая из подзадач имела в качестве входных данных связный подграф исходного графа, состоящий из вершин и соединяющих их ребер.

2 Программная реализация алгоритма

2.3 Возможные способы и особенности параллельной реализации алгоритма

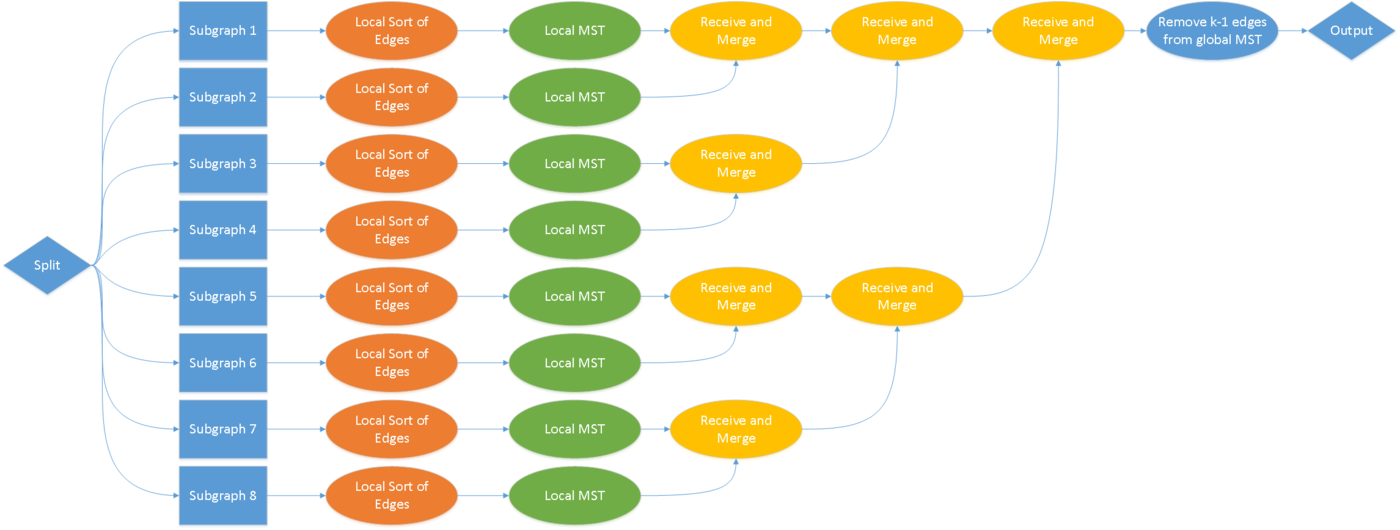
Необходимо отметить, что несмотря на всю простоту идеи распараллеливания алгоритма, описанную выше, существует несколько стратегий реализовать ее на практике. При этом, как будет показано далее, указанные стратегии дают различные приросты в производительности. Перечислим некоторые из них:

1. первая стратегия, наиболее очевидная, состоит в том, чтобы в самом начале главный процесс считал данные о ребрах и распределил считанную информацию между остальными процессами, причем каждый из них не имеет доступа к файлу с данными. Далее каждый из процессов рассчитывает локальное минимальное остовное дерево и передает его обратно главному процессу, который объединяет деревья в одно, глобальное
2. вторая стратегия во многом напоминает первую, но основное различие между ними состоит в том, что во втором случае файл с исходными данными не разделяется между процессами, а является доступным для каждого из них в полном объеме. Таким образом, каждый процесс способен считать данные о ребрах, за которые они отвечают, самостоятельно, что значительно снижает объем коммуникации между процессами. Также еще одно улучшение состоит в том, что теперь главный процесс не простаивает во время работы остальных, а, как и остальные, рассчитывает локальное минимальное остовное дерево
3. наконец, третья стратегия состоит в том, чтобы оптимизировать процесс слияния локальных минимальных остовных деревьев. Предлагается сделать так, чтобы не только главный процесс занимался слиянием, но каждый процесс участвует в процессе слияния. Для того, чтобы добиться максимальной эффективности будем предполагать, что число процессов . В этом случае потребуется шагов, чтобы выполнить слияние. На каждом шаге половина активных процессов пересылает свое локальное дерево процессу с меньшим номером на единицу, а другая половина занимается приемом и слиянием. Таким образом, через шагов главный процесс, который имеет номер 0, будет иметь в своем распоряжении глобальное минимальное остовное дерево.