Участник:Anton goy/Самоорганизующиеся карты Кохонена

Материал из Алговики
Перейти к навигации Перейти к поиску


Автор: Гой Антон, 617 группа.

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Рисунок 1. Структура самоогранизующейся карты Кохонена с шестиугольной решеткой

Самоорганизующаяся карта Кохонена (англ. Self-Organizing Map или сокращено SOM) - это разновидность нейронных сетей, относящаяся к алгоритмам обучения без учителя. Основная цель - найти скрытые закономерности в данных по средством снижения размерности исходного пространства. Важным свойством карт Кохонена является то, что они строят отображение в пространство низкой размерности (обычно двумерное) таким образом, что топология исходного пространства сохраняется. Результат данного отображения - правильная решетка из обученных нейронов - называется "картой" исходного пространства. Алгоритм был разработан известным финским учёным, заслуженным академиком Финской Академии Наук Теуво Кохоненом в 1984(2) году. Карты Кохенана находят успешное применение в задачах кластеризации и визуализации, а также для снижения размерности и детектирования аномалий в данных.

Карты Кохонена и по своей архитектуре, и по методу обучения отличаются от обычных нейронных сетей прямого распространения. C точки зрения метода обучения, карты Кохонена не используют градиентные методы для минимизации ошибки (как это делается в сетях прямого распространения), поскольку являются алгоритмом обучения без учителя и никак не могут учитывать информацию и метках классов. Поэтому нейронная сеть обучается через соревнование между нейронами: на каждом шаге алгоритма для случайного объекта из обучающей выборки выбирается нейрон-победитель (best matching unit, BMU), который в определенном смысле наиболее похож на данный объект.

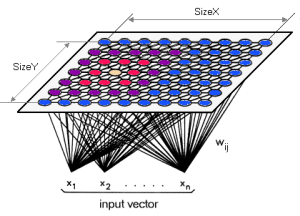
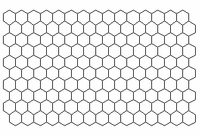
Рисунок 2б. Топология слоя Кохонена с прямоугольными ячейками
Рисунок 2а. Топология слоя Кохонена с шестиугольными ячейками

А архитектура карты Кохонена (Рис. 1) представляет два слоя: первый слой состоит из входных нейронов (их количество равно размерности исходного пространства), второй слой (его называют слоем Кохонена) представляет собой строго упорядоченную решетку, в узлах которой расположены нейроны-сумматоры, соедененные со всеми входами сети. Для визуализации топологии слоя Кохонена (Рис. 2) используют либо шестиугольные (Рис. 2а), либо прямоугольные (Рис. 2б) ячейки, в которых распологаются нейроны. Шестиугольные ячейки часто являются более предпочтительными, так как расстояние от центра выбранной ячейки до ее соседей одинаково.

Каждый нейрон [math]n_j[/math] слоя Кохонена описывается вектором весов [math]\mathbf{w}_j[/math], размерность которого совпадает с размерностью исходного пространства, и координатами нейрона на двумерной плоскости - [math]\mathbf{r}_j[/math].

Процесс обучения состоит в настройке векторов весов [math]\mathbf{w}_j[/math].

1.2 Математическое описание алгоритма

Пусть [math]\mathcal{L} = \left\{ \mathbf{x}_i \right\}_{i=1}^{N}[/math] - некоторое подмножество точек пространства [math]\mathbb{R}^D[/math], [math]\mathbf{x}_i = \left( x_{i}^{(1)}, \dots, x_{i}^{(D)} \right) \in \mathbb{R}^D[/math]. В машинном обучении множество [math]\mathcal{L}[/math] называют обучающей выборкой.

Пусть задано [math]L = X \times Y[/math] общее количество нейронов в слое Кохонена. И каждому нейрону [math]n_j[/math] поствлен в соответствие вектор весов [math]\mathbf{w}_{j} = \left( w_{j}^{(1)}, \dots, w_{j}^{(D)} \right) \in \mathbb{R}^D[/math] и вектор [math]\mathbf{r}_j \in \mathbb{R}^2[/math], определющий его положение на двумерной плоскости.

Алгоритм обучения (online version):

  1. Задать начальные приближение весов [math]\mathbf{w}_{j}[/math], [math]\forall j=1, \dots, L[/math].
  2. Выбрать случайно номер объекта [math]i \sim Unif[1, N][/math].
  3. Найти расстояние между объектом [math]\mathbf{x}_i[/math] и всеми векторами весов [math]\mathbf{w}_{j}[/math]: [math]\rho(\mathbf{x}_i, \mathbf{w}_{j}) = \left\| \mathbf{x}_i - \mathbf{w}_{j} \right\|^2, \quad \forall j=1, \dots, L[/math]
  4. Найти нейрон-победитель [math]n_b[/math], [math] b = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\mathbf{x}_i, \mathbf{w}_{j})[/math], наиболее близкий к текущему объекту [math]\mathbf{x}_i[/math].
  5. Для всех неронов [math]n_j[/math] пересчитать их веса по следующей формуле: [math]\mathbf{w}_{j} \leftarrow \mathbf{w}_{j} + \alpha(t)h_{b, j}(t)(\mathbf{x}_i - \mathbf{w}_{j})[/math], где [math]\alpha(t)[/math] - темп обучения (learning rate), монотонно убывающая функция от номера итерации [math]t[/math], [math]h_{b, j}(t)[/math] - функция определяющая "меру соседства" нейронов [math]n_b[/math] и [math]n_j[/math].
  6. Проверить критерий останова. При необходмости перейти на шаг 2.

Данное выше описание является довольно общим и не раскрывает некоторых деталей:

  • Начальное приближение для [math]\mathbf{w}_j[/math]
    • Инициализация случайными значениями. Самый простой способ - [math]w_j^{(d)} \sim Unif[0, 1][/math]. Данный подход может потребовать большое количество итераций, так как вектора весов неупорядочены и могут находится на значительном расстоянии от точек обучающей выборки.
    • Инициализация объектами обучающей выборки. Данный способ может позволить уменьшить количество итераций, так как вектора весов будут изначально находятся в области пространства, в которой расположены объекты выборки. Но проблема с неупорядоченностью остается.
    • Инициализация при помощи PCA. При помощи PCA находятся первые две главные компоненты [math]e_1, e_2[/math]. Затем в плоскости натянутой на ветора [math]e_1, e_2[/math] выбирается регулярная сетка точек, которыми и инициализируются вектора [math]\mathbf{w}_j[/math]. Этот способ является наиболее предпочтительным и на практике показывает хорошие результаты.
  • Задание [math]\alpha(t)[/math]
    • [math]\alpha(t) = \alpha_0 \exp \left\{ -\frac{t}{\lambda} \right\}[/math]
    • [math]\alpha(t) = \frac{1}{t}[/math]
    • [math]\alpha(t) = \lambda^{\frac{t}{T}}, \lambda \in (0, 1)[/math]
  • Задание [math]h_{b,j}(t)[/math]
    • Наиболее популярный способ: [math]h_{b,j}(t) = \exp \left\{ - \frac{\| \mathbf{r}_b -\mathbf{r}_j \|^2}{2\sigma(t)^2} \right\}[/math], где [math]\sigma(t)[/math] - убывающая функция.

Кроме онлайн алгоритма обучения часто на практике применяют более эффективную с точки зрения вычислений batch-версию. Пусть выбрано [math]B \in \mathbb{N}[/math]. Тогда batch-версия алгоритма описывается следующим образом:

Алгоритм обучения (batch version):

  1. Задать начальные приближение весов [math]\mathbf{w}_{j}[/math], [math]\forall j=1, \dots, L[/math].
  2. Случайно выбрать множество [math]\mathcal{B} \subset \{1, \dots, N \}[/math] размера [math]B[/math].
  3. Для каждого объекта [math]\mathbf{x}_i[/math], [math]i \in \mathcal{B}[/math], найти нейрон-победитель [math]n_{b(i)}[/math], где [math] b(i) = \arg \min_{\forall j \in \{1, \dots, L\}} \rho(\mathbf{x}_i, \mathbf{w}_{j})[/math]
  4. Пересчитать веса для всех нейронов [math]\mathbf{w}_j \leftarrow \frac{\sum_{i \in \mathcal{B}}h_{b(i),i}\mathbf{x}_i}{\sum_{i \in \mathcal{B}}h_{b(i),i}}[/math], [math]\forall j=1, \dots, L[/math].
  5. Проверить критерий останова. При необходимости перейти на шаг 2.

Интерпретация шага 2 состоит в следующем: веса нейронов преставляют собой выпуклую комбинацию объектов с номерами из [math]\mathcal{B}[/math].

1.3 Вычислительное ядро алгоритма

Рассмотрим batch-версию алгоритма. Основные вычисления приходятся на шаг 2, где необходимо вычислять расстояния между всеми [math]\mathbf{x}_i[/math], [math]i \in \mathcal{B}[/math] и весами нейронов [math]\mathbf{w}_j[/math], [math]j \in \{ 1, \dots, L \}[/math] и затем искать минимум:

[math]d_{ij} = \left\| \mathbf{x}_i - \mathbf{w}_j \right\|^2 = \left\|\mathbf{x}_i\right\|^2 - 2 \mathbf{x}_i^{T}\mathbf{w}_j + \left\|\mathbf{w}_j\right\|^2[/math]

Так как нас будет интересовать минимум по [math]j[/math], то первое слагаемое [math]\left\|\mathbf{x}_i\right\|^2[/math] можно не учитывать. Тогда все что нам нужно это вычислить матрицу квази-расстояний [math]\mathbf{D} = \| \hat{d}_{ij} \|_{B \times L}[/math], где [math]\hat{d}_{ij} = \left\|\mathbf{w}_j\right\|^2 - 2 \mathbf{x}_i^{T}\mathbf{w}_j [/math]

Сложность вычисления [math]\mathbf{D}[/math] составляет [math]O\left(L D B \right)[/math], учитывая что [math]\left\|\mathbf{w}_j\right\|^2[/math] можно вычислить за один проход по всем нейронам.

Далее поиск минимум в каждой строке матрицы [math]\mathbf{D}[/math] занимает [math]O(LB)[/math]

1.4 Макроструктура алгоритма

Пусть [math]\mathbf{X}_{\mathcal{B}}[/math] - матрица, строками которой являются объекты [math]\mathbf{x}_i[/math] таких, что [math]i \in \mathcal{B}[/math], а [math]\mathbf{W}[/math] - матрица, строками которой являются веса нейронов.

Тогда на макроуровне можно выделить следующие операции:

  1. [math]\mathbf{D} \leftarrow ComputePairwiseDistances(\mathbf{X}_{\mathcal{B}}, \mathbf{W})[/math]
  2. [math]\mathbf{b} \leftarrow FindClosestNeurons(\mathbf{D})[/math]
  3. [math]\mathbf{W} \leftarrow ComputeWeightedSumsAcrossObjects(\mathbf{X}_{\mathcal{B}}, \mathbf{b})[/math]

Здесь мы дали описание макроопераций в терминах функций, возвращающих соответствующии значения.

Функция [math]ComputePairwiseDistances[/math] вычисляет квазирасстояния между объектами и нейронами и возвращает матрицу [math]\mathbf{D} \in \mathbb{R}^{B \times L}[/math].

Функция [math]FindClosestNeurons[/math] в каждой строке матрицы [math]\mathbf{D}[/math] находит минимальное значение и возвращает вектор [math]\mathbf{b} \in \mathbb{R}^B[/math], такой что элемент в позиции [math]i[/math] соответствует номеру нейрона-победителя для объекта [math]\mathbf{x}_i[/math].

Функция [math]ComputeWeightedSumsAcrossObjects[/math] вычисляет новые значения весов для каждого нейрона, суммируя строки матрицы [math]\mathbf{X}_{\mathcal{B}}[/math] с весами пропорциональными их мере соседства с соответствующим нейроном-победителем. Неявно данная функция также использует вектор положений [math]\mathbf{r}_j[/math] нейронов на двумерной плоскости, но так как эти положения остаются неизменными в продолжении всего обучения, мы не будем указывать их явно в аргументах.

1.5 Схема реализации последовательного алгоритма

В этой секции, используя макрооперции из предыдущего раздела, дадим очень краткий псевдокод batch-версии алгоритма, который легко позволяет понимать основные строительные блоки данного алгоритма:

Рисунок 3. Способ инициализации [math]\mathbf{r}_j[/math] как узлов шестиугольных ячеек на плоскости

[math] \begin{align} \mathbf{W} := &InitializeWeights() \\ \mathbf{R} := &InitializeNeuronPositionsOnPlane() \\ \mathbf{FOR} & \ t=1 \ \mathbf{TO} \ MAX\_ITERATIONS \ \mathbf{DO} \\ & \mathcal{B} \leftarrow RandomSample\left( \{1, \dots, N\} \right) \\ & \mathbf{D} \leftarrow ComputePairwiseDistances(\mathbf{X}_{\mathcal{B}}, \mathbf{W}) \\ \quad & \mathbf{b} \leftarrow FindClosestNeurons(\mathbf{D}) \\ \quad & \mathbf{W} \leftarrow ComputeWeightedSumsAcrossObjects(\mathbf{X}_{\mathcal{B}}, \mathbf{b}) \\ \end{align} [/math]


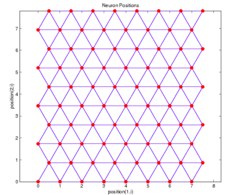
Здесь мы использовали [math]\mathbf{R} \in \mathbb{R}^{L \times 2}[/math] как обозначение для матрицы, строками которой являются [math]\mathbf{r}_j[/math]. Способ инициализации этих векторов для решетки с шестиугольными ячейками показан на Рис. 3.

Как видно из алгоритма, основной структурой данных, которая нам потребуется, будет обычная матрица, а также вектора. Стоит отметить, что алгоритм в целом неплохо оптимизируем в терминах матричных и веторных операций. Например, вычисление матрицы [math]\mathbf{D}[/math] на языке Python с использованием библиотеки оптимизированных матричных вычислений NumPy будет выглядить следующим образом: 

  W_norms = numpy.linalg.norm(W, axis=1)^2 # Вычисляем квадрат нормы для каждого вектора весов
  D = W_norms.T - 2 * numpy.dot(X, W.T) # Вычисляем матрицу квазирасстояний

А вычисление вектора [math]\mathbf{b}[/math] можно реализовать всего одной строчкой: 

  b = D.argmin(axis=1)

1.6 Последовательная сложность алгоритма

В разделе 1.3 мы уже попытались дать некоторые оценки сложности алгоритма обучения самоорганизующейся карты Кохонена. Ниже мы рассмотрим последовательную сложность более подробно.

Прежде всего необходимо понять в терминах каких операций нам следует оценить сложность алгоритма. В алгоритме преобладают арифметические операции над вещественными числами, поэтому в их терминах и будем определять сложность.

Пусть, как и ранее, [math]N[/math] - количество объектов в обучающей выборке, [math]L[/math] - количество нейронов в слое Кохонена, [math]D[/math] - размерность признакового пространства объектов (размерность векторов [math]\mathbf{x}_i[/math]) и [math]B[/math] - количество объектов в случайной подвыборке отбираемой на каждой итерации алгоритма.

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Anton_goy/Самоорганизующиеся_карты_Кохонена&oldid=5972