Алгоритм верхней релаксации численного решения двумерного уравнения Пуассона

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Разностная задача Дирихле для двумерного уравнения Пуассона, заданная в прямоугольнике [math]G=\{0\le x_1\le l_1,0\le x_2\le l_2\}[/math] с границей [math]\Gamma[/math] имеет вид :

[math] \begin{align} & \frac{\partial^2 U}{\partial x_1^2} + \frac{\partial^2 U}{\partial x_2^2} = f(x_1,x_2),(x_1,x_2) \in G,\\ & U(x_1,x_2) |_{\Gamma} = \mu (x_1,x_2).\\ \end{align} [/math]

Подобная модель может быть использована для описания установившегося течения жидкости, стационарных тепловых полей, процессов теплопередачи с внутренними источниками тепла и деформации упругих пластин и др.

Выберем пятиточечный шаблон разностной схемы "крест". На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

[math] \begin{align} &\frac{y_{i+1,j} -2y_{i,j} +y_{i-1,j}}{h_1^2} + \frac{y_{i,+1j} -2y_{i,j} +y_{i,j-1}}{h_2^2} = f_{i,j}, i= \overline{1,N_x -1},j= \overline{1,N_y -1}, \\ &y |_{\gamma_h} = \mu (x_1,x_2) |_{\gamma_h}, \\ \end{align} [/math]

где [math]\gamma_h[/math] – граничные узлы (кроме угловых узлов, они схемой не используются) .

Записанную систему линейных алгебраических уравнений относительно неизвестных [math]y_{i,j}[/math] обычно решают итерационными методами .

1.2 Математическое описание алгоритма

Рассмотрим систему линейных алгебраических уравнений:

[math] \begin{align} &\sum^{M}_{i=1} {a_{ij} u_j} = f_i. \\ \end{align} [/math]

Итерационный метод Зейделя в предположении, что диагональные элементы матрицы [math]A=(a_{ij})[/math] отличны от нуля, записывается в следующем виде:

[math] \begin{align} & \sum^{i}_{j=1} {a_{ij} y_j^{(k+1)}} + \sum^{M}_{j=i+1} {a_{ij} y_j^{(k)}} = f_i,\\ \end{align} [/math]

где [math]y_j^{(k)}[/math] − [math]j[/math]-я компонента итерационного приближения номера [math]k[/math]. В качестве начального приближения выбирается произвольный вектор.

Запишем теперь итерационный метод Зейделя в матричной форме. Для этого представим матрицу [math]A[/math] в виде суммы диагональной, нижней треугольной и верхней треугольной матриц [math]A=D+L+U[/math].

Пользуясь этими обозначениями, запишем метод Зейделя в виде

[math] \begin{align} & \left ( D+L \right )y_{k+1}+Uy_k =f, k=0,1,... \\ \end{align} [/math]

Приведем эту итерационную схему к каноническому виду двухслойных схем

[math] \begin{align} & \left ( D+L \right ) \left ( y_{k+1}-y_k \right ) +Ay_k =f, k=0,1,... \\ \end{align} [/math]

Для ускорения сходимости метода Зейделя его модифицируют, вводя в итерационную схему параметр [math]\omega[/math], так что

[math] \begin{align} & \left ( D+\omega L \right ) \frac {y_{k+1}-y_k}{\omega} +Ay_k =f, k=0,1,... \\ \end{align} [/math]

Итерационный метод при [math]\omega \gt 1[/math] называется методом верхней релаксации.

Рассмотрим применение метода верхней релаксации для нахождения приближенного решения разностной задачи Дирихле для уравнения Пуассона, заданной на сетке узлов [math] \overline {\omega_{h}} = \{ ih_1,i=0,1,...,N_x, N_x h_1 = l_1, jh_2 = 0,1,...,N_y, N_y h_2=l_2 \}[/math] в прямоугольнике [math]\overline{G} =\{0\le x\le l_1,0\le y\le l_2\}[/math]:

[math] \begin{align} & \Lambda y = \sum^{2}_{\alpha=1} {y_{\overline{x_{\alpha}}x_{\alpha}}} = -\varphi(x), x \in \overline {\omega_{h}}, y(x)= \mu (x), x \in \gamma_h.\\ \end{align} [/math]

Перед началом вычислений нужно задать начальное (например, нулевое) приближение [math]y_{i,j}^0[/math] во внутренних точках сетки и заполнить значения [math]y_{i,j}^0[/math] в граничных узлах точными значениям [math]\mu_{i,j}[/math].

Если неизвестные упорядочены по строкам сетки [math]\overline {\omega_{h}}[/math], то разностная схема может быть записана в виде следующей системы алгебраических уравнений:

[math] \begin{align} &-\frac{1}{h_1^2} y(i-1,j) - \frac{1}{h_2^2} y(i, j-1) + \left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right) y(i, j) - \frac{1}{h_1^2} y(i+1,j) - \frac{1}{h_2^2} y(i, j+1) = \varphi (i,j)\\ \end{align} [/math]

для [math]i=1,2, ... ,N_x - 1,j=1,2,... ,N_y - 1, y(x)=g(x),x \in \gamma[/math].

Такой записи оператора [math]A[/math] соответствует представление [math]A[/math] в виде суммы [math]A=D+L+U[/math], где

[math] \begin{align} & Dy= \left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right) y,\\ & Ly(i,j)=-\frac{1}{h_1^2}\dot{y}(i-1,j) - \frac{1}{h_2^2}\dot{y}(i, j-1),\\ & Uy(i,j)=-\frac{1}{h_1^2}\dot{y}(i+1,j) - \frac{1}{h_2^2}\dot{y}(i, j+1).\\ \end{align} [/math]

Метод верхней релаксации для данной системы имеет вид:

[math] \begin{align} & y_{i,j}^{l+1} = \omega \left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right)^{-1} \left(\frac{y_{i+1,j}^{l}+y_{i-1,j}^{l}}{h_1^2} + \frac{y_{i,j+1}^{l}+y_{i,j-1}^{l}}{h_2^2} -f_{i,j} \right) + \left(1- \omega \right) y_{i,j}^l,\\ & y |_{\gamma_h} = \mu (x_1,x_2) |_{\gamma_h},\\ \end{align} [/math]

где [math]\omega \in (1,2)[/math].

Вычисления начинаются с точки [math]i=1, j=1[/math] и продолжаются либо по строкам, либо по столбцам сетки. Найденное [math]y_{i,j}^{l+1}[/math] размещается на месте [math]y_{i,j}^l[/math].

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма являются множественные вычисления по формуле :

[math] \begin{align} & F\left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)= \omega \left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right)^{-1} \left(\frac{u_{i+1,j}^{l}+u_{i-1,j}^{l}}{h_1^2} + \frac{u_{i,j+1}^{l}+u_{i,j-1}^{l}}{h_2^2} -f_{i,j} \right) +(1- \omega)u_{i,j}^l. \end{align} [/math]

1.4 Макроструктура алгоритма

Основную макрооперацию составляют вычисления .

1.5 Схема реализации последовательного алгоритма

do l = 1, [math]r_{it}[/math]
 do i = 1, [math]N_x-1[/math]
   do j = 1, [math]N_y-1[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
 enddo
enddo

1.6 Последовательная сложность алгоритма

Для реализации метода верхней релаксации требуется порядка

• [math]4r_{it}\left(N_{x}-1\right) \left(N_{y}-1\right)[/math] умножений;
• [math]4r_{it}\left(N_{x}-1\right) \left(N_{y}-1\right)[/math] сложений и вычитаний.

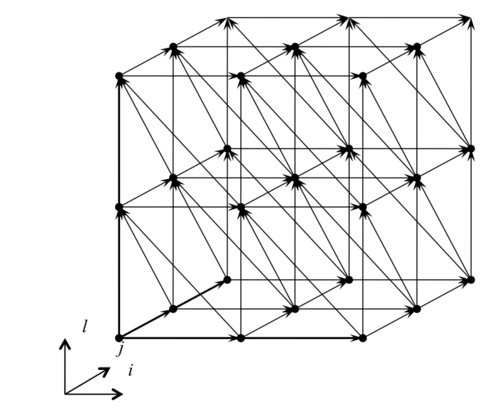
1.7 Информационный граф

Все зависимости алгоритма метода верхней релаксации являются однородными и выражаются векторами зависимостей (0,1,0), (0,0,1), (1,0,0), (1,0,–1), (1,–1,0) . В случае метода Зейделя вектор истинных зависимостей (1,0,0) отсутствует.

Рисунок 1 - Схематичнское изображение зависимостей алгоритма верхней релаксации

1.8 Ресурс параллелизма алгоритма

Алгоритм верхней релаксации обладает, так называемым, скошенным параллелизмом.

1.9 Входные и выходные данные алгоритма

Входные данные: матрица F (элементы [math]f_{ij}[/math]), вектор [math]\mu[/math], параметр [math]\omega[/math].

Выходные данные: матрица y (элементы [math]y_{ij}[/math]).

Объём выходных данных: [math]\left(N_{x}-1\right) \left(N_{y}-1\right)[/math].

1.10 Свойства алгоритма

Найдем оптимальное значение [math]\omega_{0}[/math] параметра [math]\omega[/math]. Для этого необходимо найти или оценить снизу минимальное собственное значение задачи (собственное значение задачи – определенные значения, при которых решение задачи существует)  :

[math] \begin{align} & y_{\overline{x_1}x_1} + y_{\overline{x_2}x_2} + \lambda \left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right)y=0, y(x)=0, x \in \gamma_h. \end{align} [/math]

Так как собственные значения разностного оператора Лапласа [math]\Lambda y = y_{\overline{x_1}x_1} + y_{\overline{x_2}x_2}[/math] известны

[math] \begin{align} & \dot \lambda_k = \frac{4}{h_1^2} \sin^2 \frac{k_1 \pi h_1}{2l_1} + \frac{4}{h_2^2} \sin^2 \frac{k_2 \pi h_2}{2l_2}, k_{\alpha} = 1,2,..., N_{\alpha} -1, \end{align} [/math]

то

[math] \begin{align} & \lambda_k = \frac {\dot \lambda_k} {\left(\frac{2}{h_1^2} + \frac{2}{h_2^2} \right)} = \frac{2h_2^2}{h_1^2+h_2^2} \sin^2 \frac{k_1 \pi h_1}{2l_1} + \frac{2h_1^2}{h_1^2+h_2^2} \sin^2 \frac{k_2 \pi h_2}{2l_2}. \end{align} [/math]

Следовательно,

[math] \begin{align} & \lambda_{min} = \frac{2h_2^2}{h_1^2+h_2^2} \sin^2 \frac{k_1 \pi h_1}{2l_1} + \frac{2h_1^2}{h_1^2+h_2^2} \sin^2 \frac{k_2 \pi h_2}{2l_2} \end{align} [/math]

и параметр [math]\omega_{0}[/math] находится по формуле

[math] \begin{align} & \omega_{0} = \frac{2}{1+\sqrt{\lambda_{min} \left( 2- \lambda_{min}\right)}} \in \left(1, 2 \right). \end{align} [/math]

В частном случае, когда [math]G+\Gamma[/math] – квадрат со стороной [math]l[/math] и сетка квадратная [math]\left( N_1=N_2=N_3 \right)[/math] имеем

[math] \begin{align} & \omega_{0} = \frac{2}{1+ \sin \frac{\pi}{N}}. \end{align} [/math]

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений [math]u_{i,j}[/math] не станут меньше некоторой требуемой точности вычислений.

Известно , что если оператор [math]A[/math] самосопряжен и положительно определен, а параметр [math]\omega[/math] удовлетворяет условию [math]0\lt \omega \lt 2[/math], то метод верхней релаксации сходится.

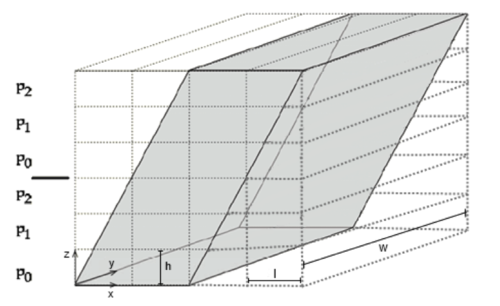
Существует блочный алгоритм, использующий скошенные циклы. Для получения блочного алгоритма используется тайлинг. Тайлинг (выделение макроопераций для получения алгоритмов блочного типа) применяется для построения эффективных параллельных алгоритмов и для уменьшения накладных расходов на использование иерархической памяти.

Для осуществления тайлинга трехмерного гнезда циклов надо выбрать три семейства гиперплоскостей и разбить итерационное пространство на макрооперации-тайлы. Семейства гиперплоскостей должны быть такими, чтобы макрооперации могли выполняться атомарно, как одна единица вычислений (допустимость тайлинга). Для генерации кода применяется предварительное аффинное преобразование итерационного пространства, при котором гиперплоскости, ограничивающие тайлы, становятся параллельными координатным плоскостям; далее применяется стандартная техника преобразования каждого цикла в двумерную циклическую конструкцию.

Использование тайлов предполагает уменьшение расходов на обмен данными между процессорами, адаптацию алгоритма к использованию иерархической памяти одного процессора.

Будем использовать семейства гиперплоскостей, задаваемые ортогональными гиперплоскостям векторами (1,0,0), (1,1,0), (1,0,1). Такой набор гиперплоскостей позволяет с минимально возможными скосами циклов произвести тайлинг по всем трем координатам.

Каждый из векторов (1,0,0), (1,1,0), (1,0,1) ортогонален двум из пяти векторов зависимостей (0,1,0), (0,0,1), (1,0,0), (1,0,–1), (1,–1,0): вектор (1,0,0) ортогонален векторам зависимостей (0,1,0), (0,0,1), вектор (1,1,0) ортогонален векторам зависимостей (0,0,1), (1,–1,0), вектор (1,0,1), ортогонален векторам зависимостей (0,1,0), (1,0,–1). Теоретически считается, что чем больше плоскость «включает в себя» векторов зависимостей, тем лучше: информационный разрез, порождаемый плоскостью, не приводит к передаче информации по соответствующему направлению.

Осуществим предварительное аффинное преобразование [math]\left( l,i,j \right) \rightarrow \left( i_1,i_2,i_3 \right)[/math] итерационного пространства, задаваемое равенствами [math]i_1=l, i_2=l+i, i_3=l+j[/math].

Для этого выразим исходные координаты через новые координаты: [math] l=i_1, i=i_2 - i_1, j= i_3 - i_1[/math].

Из системы неравенств [math]1 \le i_1 \le r_{it}, 1 \le i_2-i_1 \le N_x-1, 1 \le i_3-i_1 \le N_y - 1[/math] получим области изменения параметров преобразованного алгоритма: [math]1 \le i_1 \le r_{it}, i_1+1 \le i_2 \le i_1 + N_x-1, i_1 +1 \le i_3 \le i_1 + N_y - 1[/math].

Таким образом, в результате аффинного преобразования приходим к следующему гнезду циклов:

do [math]i_1 = 1, r_{it}[/math]
 do [math]i_2 =i_1 + 1, i_1 +N_x-1[/math]
   do [math]i_3 =i_1 + 1, i_1 + N_y-1[/math]
    [math]i=i_2-i_1[/math]
    [math]j=i_3-i_1[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
 enddo
enddo

Зависимости теперь задаются векторами (0,1,0), (0,0,1), (1,1,1), (1,1,0), (1,0,1) с неотрицательными координатами, поэтому тайлинг допустим.

Осуществим тайлинг – преобразуем каждый цикл в двумерную циклическую конструкцию. Каждый цикл разбивается на глобальный и локальный: глобальные циклы определяют порядок вычисления тайлов, локальные циклы определяют порядок вычисления итераций исходного алгоритма в границах одного тайла.

Пусть [math]r_1, r_2, r_3[/math] – параметры размеров (без учета границ области итераций) тайла, [math]Q_1, Q_2, Q_3[/math] – число тайлов по измерениям. Так как число гиперплоскостей вдоль координат [math]i_1, i_2, i_3[/math] равно соответственно [math]r_{it}, r_{it}+N_x-2, r_{it}+N_y-2[/math], то [math]Q_1 = \left \lceil \frac{r_{it}}{r_1} \right \rceil, Q_2 = \left \lceil \frac{r_{it}+N_x-2}{r_2} \right \rceil, Q_3 = \left \lceil \frac{r_{it}+N_y-2}{r_3} \right \rceil[/math]. Используется метод окаймления преобразованной области итераций: итерационная область окаймляется прямоугольным параллелепипедом, затем окаймляющая область разбивается на [math]Q_1 \times Q_2 \times Q_3[/math] тайлов (допускаются избыточные области изменения параметров глобальных циклов). После разбиения циклов и перестановки циклов получим:

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]i_2^{gl} = 0, Q_2-1[/math]
  do [math]i_3^{gl} = 0, Q_3-1[/math]
   do [math]i_1 = \left( 1+ i_1^{gl}r_1 \right), min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right)[/math]
    do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1 +1 \right), min \left( 1 + \left( i_2^{gl} +1 \right)r_2, i_1+N_x-1 \right)[/math]
     do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1 +1 \right), min \left( 1 + \left( i_3^{gl} +1 \right)r_3, i_1+N_y-1 \right)[/math]
      [math]i=i_2-i_1[/math]
      [math]j=i_3-i_1[/math]
      [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
     enddo
    enddo
   enddo
  enddo
 enddo
enddo

Таким образом, получен зернистый (т.е. блочный) алгоритм

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]i_2^{gl} = 0, Q_2-1[/math]
  do [math]i_3^{gl} = 0, Q_3-1[/math]
   [math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math]
  enddo
 enddo
enddo

где [math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math] задается следующим образом:

do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right)[/math]
 do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1 +1 \right), min \left( 1 + \left( i_2^{gl} +1 \right)r_2, i_1+N_x-1 \right)[/math]
  do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1 +1 \right), min \left( 1 + \left( i_3^{gl} +1 \right)r_3, i_1+N_y-1 \right)[/math]
   [math]i=i_2-i_1[/math]
   [math]j=i_3-i_1[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddo
 enddo
enddo

Получим еще блочный алгоритм, использующий тайлинг с перекрытиями.

Применим к алгоритму тайлинг с перекрытиями размера [math]m_{over}[/math]. Для этого применим обычный (без перекрытий) тайлинг по трем координатам и на каждой итерации [math]l[/math] припишем тайлам примыкающие к каждой из их границ необходимое число, определяемое зависимостями алгоритма, продублированных итераций [math]i[/math] и [math]j[/math].

Для осуществления обычного тайлинга приходилось производить такое предварительное аффинное преобразование, чтобы все координаты векторов зависимостей стали неотрицательными. Это приводило к скашиванию циклов. Тайлинг с перекрытиями осуществляется без скашивания циклов. Основным преимуществом получаемых зернистых алгоритмов считается возможность одновременно начинать выполнение операций многих тайлов, в то время как после скашивания требуется, как правило, разгон вычислений. Будем требовать, чтобы каждый трехмерный гало-тайл мог выполняться независимо от других гало-тайлов, включающих операции тех же итераций [math]l[/math] алгоритма . Операции одной итерации [math]l[/math] назовем ярусом вычислений.

Каждый гало-тайл выполняет вычисления в основных ячейках и на четырех границах (с левой, верхней, правой, нижней стороны). Наличие векторов зависимостей (1,1,0), (1,0,1), (1,–1,0), (1,0,–1) приводит к тому, что если используется перекрытие размера [math]m_{over}[/math], то перекрытие такого размера должно быть с каждой из четырех сторон и должно выполняться [math]r_1=m_{over}+1[/math].

Полученный алгоритм можно представить следующим образом:

do [math]l^{gl} = 0, Q_1-1[/math]
 do [math]i^{gl} = 0, Q_2-1[/math]
  do [math]j^{gl} = 0, Q_3-1[/math]
   [math]Tile^{halo} \left( l^{gl}, i^{gl}, j^{gl} \right)[/math]
  enddo
 enddo
enddo,

где [math]Tile^{halo} \left( l^{gl}, i^{gl}, j^{gl} \right)[/math] вычисляется по формуле

do [math]l = 1+ l^{gl}r_1 , min \left( \left( l^{gl} +1 \right)r_1, r_{it} \right)[/math]
 do [math]i = max \left( l- \left( l^{gl}+1 \right)r_1 + i^{gl}r_2 +1, 1 \right), min \left(-l+ \left( l^{gl} +1 \right) r_1 + \left( i^{gl} +1 \right)r_2, N_x-1 \right)[/math]
  do [math]j = max \left( l- \left( l^{gl}+1 \right)r_1 + j^{gl}r_3 +1, 1 \right), min \left(-l+ \left( l^{gl} +1 \right) r_1 + \left( j^{gl} +1 \right)r_3, N_y-1 \right)[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddo
 enddo
enddo

2.2 Локальность данных и вычислений

y В методе верхней релаксации на всех вхождениях имеется пространственная локальность (предполагается, что хранение в памяти элементов массивов осуществляется по строкам). В то же время, есть следующая несогласованность использования кэш-линеек, порождаемых вхождениями [math]u_{i-1,j},u_{i,j},u_{i+1,j}[/math].

Пусть [math]N[/math] достаточно большое. Тогда при фиксированных [math]i[/math] и [math]j[/math] множества элементов трех кэш-линеек, содержащих [math]u_{i-1,j},u_{i,j},u_{i+1,j}[/math], не пересекаются. Если увеличить [math]i[/math] на единицу, то в двух из трех линеек содержимое уже побывало в кэше, но к моменту нового использования из кэша исчезло и требует новой загрузки из оперативной памяти. Кроме того, на каждой новой итерации [math]l[/math] обновленные элементы массивов снова будут загружаться в кэш.

Универсальным способом улучшения локальности данных является тайлинг. Можно воспользоваться зернистым алгоритмом, использующим скошенные циклы, или зернистым алгоритмом, использующим тайлинг с перекрытиями. В этих блочных модификациях алгоритма данные, загружаемые в кэш, используются на разных вхождениях согласованно.

2.3 Возможные способы и особенности параллельной реализации алгоритма

Рассмотрим алгоритмы, которые можно использовать для OpenMP-реализаций на многоядерном CPU. Первый алгоритм, назовем его точечным параллельным алгоритмом, задает независимые вычисления в ячейках 2D расчетной сетки. Второй алгоритм, блочного типа, задает скошенный параллелизм уровня тайлов. Третий алгоритм также имеет блочный тип и использует блоки с перекрытием (блоки с избыточными вычислениями); каждый блок охватывает несколько ярусов и организован таким образом, что все вычисления блока можно производить без обращения к результатам вычислений других многоярусных блоков.

Точечный параллельный алгоритм. Наиболее простой параллельный алгоритм для реализации на многоядерных компьютерах с общей памятью можно получить, если считать, что на каждой итерации происходят независимые вычисления в ячейках 2D расчетной сетки:

do [math]l = 1, r_{it}[/math]
 dopar [math]i = 1, N_x-1[/math]
  dopar [math]j = 1, N_y-1[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddopar
 enddopar
enddopar

Для получения потоков (нитей) вычислений используются параллельные циклы алгоритмов. На каждой текущей итерации [math]l[/math] можно вычисления в ячейке [math](i,j)[/math] выполнять независимо от вычислений в других ячейках, если допустить использование как обновленных, так и полученных на предыдущей итерации элементов массива [math]u[/math].

В работе рассматриваются проблемы организации потоков вычислений, связанные с оценкой погрешности такого итерационного процесса.

Блочный параллельный алгоритм, использующий скошенный параллелизм уровня тайлов. Из анализа зависимостей (координаты векторов зависимостей являются неотрицательными) следует, что для каждого фиксированного [math]i_1^{gl}[/math] можно одновременно и независимо выполнять итерации [math]\left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right) [/math] циклов такие, что [math]i_2^{gl}+ i_3^{gl} =t[/math], где [math]t[/math] является фиксированным числом:

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]t = 0, Q_2 + Q_3-2[/math]
  dopar [math]i_2^{gl} = 0, Q_2-1[/math]
   dopar [math]i_3^{gl} = 0, Q_3-1[/math]
    if [math]i_2^{gl}+ i_3^{gl} =t[/math] then
     [math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math]
   enddopar
  enddopar
 enddopar
endodopar

[math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math] имеет вид .

Алгоритм с явно заданным параллелизмом можно представить еще в следующем виде:

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]t = 0, Q_2 + Q_3-2[/math]
  dopar [math]i_3^{gl}= max \left( 0,t-Q_2+1 \right), min \left( t, Q_3-1 \right)[/math]
   [math]i_2^{gl}=t-i_3^{gl}[/math]
   [math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math]
  enddopar
 enddo
enddo

Такая запись является следствием аффинного преобразования алгоритма : [math]\left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right) \rightarrow \left( i_1^{gl}, t, i_3^{gl} \right), t=i_2^{gl}+i_3^{gl}[/math].

Алгоритмы и имеют параллельные циклы, поэтому могут быть использованы для OpenMP-реализаций на многоядерных компьютерах. Если использовать алгоритм , получим

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]t = 0, Q_2 + Q_3-2[/math]
  dopar [math]i_3^{gl}= max \left( 0,t-Q_2+1 \right), min \left( t, Q_3-1 \right)[/math]
   [math]Thread \left( i_1^{gl}, t, i_3^{gl} \right)[/math]
  enddopar
 enddo
enddo

где [math]Thread \left( i_1^{gl}, t, i_3^{gl} \right)[/math] задается следующим образом:

[math][/math]
 do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right)[/math]
  do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1+1 \right), min \left(1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
   do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1+1 \right), min \left(1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
    [math]i=i_2-i_1[/math]
    [math]j=i_3-i_1[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
  enddo
 enddo

Блочный параллельный алгоритм, использующий тайлинг с перекрытиями. Алгоритм , реализующий модифицированный алгоритм , можно для каждого параметра [math]l^{gl}[/math] внешнего цикла представить независимо выполняемыми гало-тайлами:

do [math]l^{gl} = 0, Q_1-1[/math]
 dopar [math]i^{gl} = 0, Q_2-1[/math]
  dopar [math]j^{gl} = 0, Q_3-1[/math]
   [math]Tile^{halo} \left( l^{gl}, i^{gl}, j^{gl} \right)[/math]
  enddopar
 enddopar
enddo

где [math]Tile^{halo} \left( l^{gl}, i^{gl}, j^{gl} \right)[/math] имеет вид . Параллельные циклы могут быть использованы для организации параллельных потоков вычислений.

В частности, если в алгоритме потоки задает только цикл с параметром [math]i^{gl}[/math], то получим

do [math]l^{gl} = 0, Q_1-1[/math]
 dopar [math]i^{gl} = 0, Q_2-1[/math]
  [math]Thread \left( l^{gl}, i^{gl} \right)[/math]
 enddopar
enddo

Поток [math]Thread \left( l^{gl}, i^{gl} \right)[/math] включает в себя операции гало-тайлов [math]Tile^{halo} \left( l^{gl}, i^{gl}, j^{gl} \right), j^{gl}=0,1,...,Q_3-1[/math]:

do [math]j^{gl} = 0, Q_3-1[/math]
 do [math]l = 1+ l^{gl}r_1 , min \left( \left( l^{gl} +1 \right)r_1, r_{it} \right)[/math]
  do [math]i = max \left( l- \left( l^{gl}+1 \right)r_1 + i^{gl}r_2 +1, 1 \right), min \left(-l+ \left( l^{gl} +1 \right) r_1 + \left( i^{gl} +1 \right)r_2, N_x-1 \right)[/math]
   do [math]j = max \left( l- \left( l^{gl}+1 \right)r_1 + j^{gl}r_3 +1, 1 \right), min \left(-l+ \left( l^{gl} +1 \right) r_1 + \left( j^{gl} +1 \right)r_3, N_y-1 \right)[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
  enddo
 enddo
enddo

Зададим в алгоритме , вычисления, порождаемые оценкой погрешности итерационного процесса. Каждый поток формирует локальную оценку погрешности dthread. После завершения вычислений поток сравнивает свою оценку dthread с общей оценкой погрешности dmax. Итерации [math]i_1^{gl}[/math] внешнего цикла выполняются до тех пор, пока dmax не станет меньше заданной величины [math]\varepsilon[/math] или пока не будет достигнуто предельное число итераций.

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]t=0, Q_2+Q_3-2[/math]
  [math]dmax = 0[/math]
  dopar [math]i_3^{gl}=max \left( 0, t- Q_2+1 \right), min \left( t, Q_3-1 \right)[/math]
   [math]Thread \left( i_1^{gl}, t ,i_3^{gl} \right)[/math]
  enddopar
 enddo
 if [math]\left( dmax\lt  \varepsilon \right) i_1^{gl}=Q_1-1[/math]
enddo

Поток [math]Thread \left( i_1^{gl}, t ,i_3^{gl} \right)[/math] теперь не только включает в себя операции тайлов, но и формирует локальную оценку погрешности, используя две последние итерации тайлов [math]i=min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right) -1 [/math] и [math]i=min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right)[/math]:

[math]dthread=0[/math]
[math]i_2^{gl} = t- i_3^{gl} [/math]
 do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right) -1[/math]
  do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1+1 \right), min \left(1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
   do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1+1 \right), min \left(1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
    [math]i=i_2-i_1[/math]
    [math]j=i_3-i_1[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
  enddo
 enddo
 do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1+1 \right), min \left(1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
  do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1+1 \right), min \left(1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
   [math]i=i_2-i_1[/math]
   [math]j=i_3-i_1[/math]
   [math]u_{temp}=u(i,j)[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   [math]d=\left | u_{temp}-u(i,j) \right |[/math]
   if (dthread < d) dthread = d
  enddo
 enddo
enddo
if (dmax < dthread) dmax = dthread

Алгоритмы и можно использовать для получения реализаций на графических ускорителях. Для реализации алгоритма на графическом процессоре множество операций алгоритма должно быть разбито на блоки, а блоки – на потоки (нити) вычислений.

Применим технику двухуровневого тайлинга. Множество операций алгоритма разобьем на блоки вычислений путем обычного тайлинга (тайлинг первого уровня) и укажем блоки, которые можно выполнять независимо друг от друга. Разбиение блоков вычислений на потоки вычислений произведем путем повторного применения тайлинга (тайлинг второго уровня). Разбиения должны производиться таким образом, чтобы потоки одного блока могли выполняться параллельно (не обязательно независимо, возможно взаимодействие посредством разделяемой памяти и синхронизации).

Если использовать алгоритм , то блоки вычислений (обозначим их [math]Bl \left( i_3^{gl} \right)[/math] – это тайлы [math]Tile \left( i_1^{gl}, i_2^{gl}, i_3^{gl} \right)[/math] при [math]i_2^{gl}=t- i_3^{gl}[/math] и фиксированных [math]i_1^{gl}[/math] и [math]t[/math]. При фиксированных параметрах [math]i_1^{gl}[/math] и [math]t[/math] внешних циклов, независимо друг от друга можно выполнять блоки [math]Bl \left( i_3^{gl} \right)[/math] на итерациях параллельного цикла:

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]t=0, Q_2+Q_3-2[/math]
  запуск ядра
  dopar [math]i_3^{gl}=max \left( 0, t- Q_2+1 \right), min \left( t, Q_3-1 \right)[/math]
    [math]Bl \left( i_3^{gl} \right)[/math]
  enddopar
 enddo
enddo

где [math]Bl \left( i_3^{gl} \right)[/math]:

[math]i_2^{gl} = t- i_3^{gl} [/math]
do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_3^{gl} +1 \right)r_3, r_{it} \right)[/math]
 do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1+1 \right), min \left(1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
  do [math]i_3 = max \left( 2+ i_3^{gl}r_3, i_1+1 \right), min \left(1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
   [math]i=i_2-i_1[/math]
   [math]j=i_3-i_1[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddo
 enddo
enddo

Для организации потоков вычислений произведем повторное разбиение блоков вычислений [math]Bl \left( i_3^{gl} \right)[/math]. Обозначим через [math]r_{1,2}, r_{2,2}, r_{3,2}[/math] размеры тайлов второго уровня.

Рассмотрим тайлинг, для которого цикл [math]i_1[/math] блока вычислений является локальным не разбиваемым: [math]r_{1,2}=r_1[/math]. Циклы [math]i_2[/math] и [math]i_3[/math] разбиваются, числа [math]Q_{2,2} = \left \lceil \frac{r_2}{r_{2,2}} \right \rceil, Q_{3,2} = \left \lceil \frac{r_3}{r_{3,2}} \right \rceil[/math] задают количество итераций в новых циклах с параметрами [math]i_2^{gl2}[/math] и [math]i_3^{gl2}[/math] соответственно. Так как [math]r_{1,2}=r_1[/math], то [math]Q_{1,2} = \left( \lceil \frac{r_1}{r_{1,2}} \right) \rceil = 1 [/math], цикл do [math]i_1^{gl2} = 0, Q_{1,2}-1[/math] с параметром [math]i_1^{gl2}[/math] является вырожденным, [math]i_1^{gl2}=0[/math]. После разбиения и перестановки циклов получим следующее представление блока вычислений [math]Bl \left( i_3^{gl} \right)[/math]:

[math]i_2^{gl} = t- i_3^{gl} [/math]
do [math]i_2^{gl2} = 0, Q_{2,2}-1[/math]
 do [math]i_3^{gl2} = 0, Q_{3,2}-1[/math] 
  do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_3^{gl} +1 \right)r_3, r_{it} \right)[/math]
   do [math]i_2 = max \left( 2+ i_2^{gl}r_2 +  i_2^{gl2}r_{2,2}, i_1+1 \right), min \left(1 + i_2^{gl}r_2 + \left( i_2^{gl2} +1 \right) r_{2,2},1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
    do [math]i_3 = max \left( 2+ i_3^{gl}r_3 +  i_3^{gl2}r_{3,2}, i_1+1 \right), min \left(1 + i_3^{gl}r_3 + \left( i_3^{gl2} +1 \right) r_{3,2},1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
     [math]i=i_2-i_1[/math]
     [math]j=i_3-i_1[/math]
     [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
    enddo
   enddo
  enddo
 enddo'
enddo

Все потоки одного блока вычислений должны выполняться параллельно, поэтому организовать потоки таким же образом, как и блоки вычислений нельзя: при использовании скошенного параллелизма параллельно могут выполняться не все тайлы блока, а только тайлы с одинаковым значением параметра t. В то же время, параллельные потоки не обязательно должны выполняться независимо. Достаточно независимого выполнения только фрагментов потоков, затем, после обмена данными (посредством разделяемой памяти и синхронизации), следующих фрагментов.

Любые итерации циклов [math]i_2^{gl2}[/math], [math]i_3^{gl2}[/math] могут выполняться независимо при одном и том следующим образом. Поэтому параллельно выполняемые потоки можно задать при фиксированных значениях [math]i_2^{gl2}[/math], [math]i_3^{gl2}[/math] после каждой итерации [math]i_1[/math] требуется синхронизация потоков. Так как потоки не являются независимыми, то для указания одновременно выполняемых потоков блока [math]Bl \left( i_3^{gl} \right)[/math] оператор dopar использовать не будем.

do [math]i_2^{gl2} = 0, Q_{2,2}-1[/math]
 do [math]i_3^{gl2} = 0, Q_{3,2}-1[/math]
  [math]Thr \left ( i_2^{gl2}, i_3^{gl2} \right )[/math].

Поток вычислений [math]Thr \left ( i_2^{gl2}, i_3^{gl2} \right )[/math] имеет следующий вид:

[math]i_2^{gl} = t- i_3^{gl} [/math]
 do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_3^{gl} +1 \right)r_3, r_{it} \right)[/math]
 do [math]i_2 = max \left( 2+ i_2^{gl}r_2 +  i_2^{gl2}r_{2,2}, i_1+1 \right), min \left(1 + i_2^{gl}r_2 + \left( i_2^{gl2} +1 \right) r_{2,2},1+ \left( i_2^{gl} +1 \right) r_2 ,i_1+ N_x-1 \right)[/math]
  do [math]i_3 = max \left( 2+ i_3^{gl}r_3 +  i_3^{gl2}r_{3,2}, i_1+1 \right), min \left(1 + i_3^{gl}r_3 + \left( i_3^{gl2} +1 \right) r_{3,2},1+ \left( i_3^{gl} +1 \right) r_3 ,i_1+ N_y-1 \right)[/math]
   [math]i=i_2-i_1[/math]
   [math]j=i_3-i_1[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddo
 enddo
enddo

Для метода верхней релаксации также получим алгоритм с 3D тайлами, для реализации на суперкомпьютерах с распределенной памятью, следуя методике работы построения параллельных алгоритмов для выполнения шаблонных вычислений зейделевского типа. Эта методика позволяет выбрать предварительное преобразование алгоритма (скос по одной из координат итерационного пространства), размеры зерна вычислений (задающего макрооперации алгоритма), отображение макроопераций на параллельные вычислительные процессы, учитывающее специфику итерационных алгоритмов.

Осуществим предварительное аффинное преобразование [math]\left( l,i,j \right) \rightarrow \left( i_1,i_2,i_3 \right)[/math] итерационного пространства, задаваемое равенствами [math]i_1=l, i_2=l+i, i_3=j[/math].

В результате аффинного преобразования алгоритма приходим к следующему гнезду циклов:

do [math]i_1 = 1, r_{it}[/math]
 do [math]i_2 =i_1 + 1, i_1 +N_x-1[/math]
   do [math]i_3 =i_1 + 1, i_1 + N_y-1[/math]
    [math]i=i_2-i_1[/math]
    [math]j=i_3-i_1[/math]
    [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
   enddo
 enddo
enddo

Осуществим тайлинг – преобразуем каждый из двух внешних циклов в двумерную циклическую конструкцию. Каждый из этих циклов разбивается на глобальный и локальный: глобальные циклы определяют порядок вычисления тайлов, локальные циклы определяют порядок вычисления итераций исходного алгоритма в границах одного тайла. Самый внутренний цикл не разбивается (тайлинг по координате [math]i_3[/math] недопустим) и считается локальным. Пусть [math]r_1, r_2, r_3 \left ( r_3=N_y-1 \right )[/math] параметры размеров тайла (без учета границ области итераций), [math]Q_1, Q_2, Q_3[/math] – число тайлов по измерениям. Так как число гиперплоскостей вдоль координат [math]i_1, i_2, i_3[/math] равно соответственно [math]r_{it}, r_{it}+N_x-2, r_{it}+N_y-1[/math], то [math]Q_1 = \left \lceil \frac{r_{it}}{r_1} \right \rceil, Q_2 = \left \lceil \frac{r_{it}+N_x-2}{r_2} \right \rceil, Q_3 = \left \lceil \frac{r_{it}+N_y-1}{r_3} \right \rceil = 1[/math]. Используется метод окаймления преобразованной области итераций: итерационная область окаймляется прямоугольным параллелепипедом, затем окаймляющая область разбивается на [math]Q_1 \times Q_2 \times Q_3[/math] тайлов (допускаются избыточные области изменения параметров глобальных циклов). После разбиения циклов и перестановки циклов получим:

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]i_2^{gl} = 0, Q_2-1[/math]
  do [math]i_1 = \left( 1+ i_1^{gl}r_1 \right), min \left( \left( i_3^{gl} +1 \right)r_3, r_{it} \right)[/math]
   do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1 +1 \right), min \left( 1 + \left( i_2^{gl} +1 \right)r_2, i_1+N_x-1 \right)[/math]
    do [math]i_3 = 1, N_y-1[/math]
     [math]i=i_2-i_1[/math]
     [math]j=i_3[/math]
     [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
    enddo
   enddo
  enddo
 enddo
enddo

Таким образом, получен зернистый алгоритм

do [math]i_1^{gl} = 0, Q_1-1[/math]
 do [math]i_2^{gl} = 0, Q_2-1[/math]
  do [math]i_3^{gl} = 0, Q_3-1[/math]
   [math]Tile \left( i_1^{gl}, i_2^{gl}, 1 \right)[/math]
  enddo
 enddo
enddo

где [math]Tile \left( i_1^{gl}, i_2^{gl}, 1 \right)[/math] задается следующим образом:

do [math]i_1 = 1+ i_1^{gl}r_1 , min \left( \left( i_1^{gl} +1 \right)r_1, r_{it} \right)[/math]
 do [math]i_2 = max \left( 2+ i_2^{gl}r_2, i_1 +1 \right), min \left( 1 + \left( i_2^{gl} +1 \right)r_2, i_1+N_x-1 \right)[/math]
  do [math]i_3 = 1, N_y-1[/math]
   [math]i=i_2-i_1[/math]
   [math]j=i_3[/math]
   [math]u(i,j)=F \left(u_{i-1,j},u_{i,j-1},u_{i,j},u_{i+1,j},u_{i,j+1}\right)[/math]
  enddo
 enddo
enddo

Пусть P - число процессов, предназначенных для реализации трехмерного цикла. Единый для каждого из P процессов псевдокод параллельного алгоритма можно записать следующим образом (p - номер процесса):

Для каждого процесса [math]\Rho r _p, 0 \le p \le \Rho - 1[/math]:

do [math]i_1^{gl} = p, Q_1-1, \Rho [/math]
 do [math]i_2^{gl} = 0, Q_2-1[/math]
  [math]Tile \left( i_1^{gl}, i_2^{gl}, 1 \right)[/math]
 enddo
enddo

Рисунок 2- Распределение тайлов преобразованного алгоритма между параллельными процессами

Ввести вычисления для оценки погрешности итерационного процесса можно следующим образом. Каждый процесс для каждого фиксированного [math]i_1^{gl}[/math] формирует локальную оценку погрешности, используя две последние итерации тайла [math]l = \left ( i_1^{gl} +1 \right )r_1[/math] и [math]l = \left ( i_1^{gl} +1 \right )r_1 - 1[/math]. Итерирование ведется до тех пор, пока хотя бы для одного процесса локальная оценка не станет меньше заданной величины ε или пока не будет достигнуто предельное число итераций.

2.6 Выводы для классов архитектур

Эффективное выполнение алгоритма возможно на вычислительных устройствах с ускорителем GPU, суперкомпьютерах с распределенной памятью и многоядерных компьютерах с общей памятью.

2.7 Существующие реализации алгоритма

Алгоритм верхней релаксации реализован в языке Matlab.

3 Литература

Примечания