Участник:BDA/Ортогонализация Грама-Шмидта
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Frolov и ASA. |
| Ортогонализация Грама-Шмидта | |
| Последовательный алгоритм | |
| Последовательная сложность | O(nm^2) |
| Объём входных данных | nm |
| Объём выходных данных | nm |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | O(nm) |
| Ширина ярусно-параллельной формы | O(m) |
Основные авторы описания: Белов Н. А. (пункты 1.3, 1.4, 1.5, 1.6, 1.9, 1.10, 2.4, 2.7, 3), Богомолов Д. А. (пункты 1.1, 1.2, 1.6, 1.7, 1.8, 2.4, 3).
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Ортогонализация ― алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V.
Ортогонализация Грама–Шмидта[1] (процесс Грама–Шмидта) ― наиболее известный алгоритм ортогонализации. Назван в честь Йоргена Педерсена Грама[2] и Эрхарда Шмидта[3], однако ранее уже появлялся в работах Лапласа и Коши. Является частным случаем разложения Ивасавы, так как может быть представлен как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами.
Рассматриваемый алгоритм применяется для борьбы с помехами в адаптивной системе селекции движущихся целей[4], в протоколах безопасности[5], для повышения экономичности алгоритмов оценивания параметров моделей объектов управления[6] и в других областях.
1.2 Математическое описание алгоритма
Входные данные. m линейно независимых векторов \mathbf{a}_1,...,\mathbf{a}_m c размерностью пространства n, записанных в матрице A с элементами \alpha_{ij}.
Выходные данные. m ортогональных векторов \mathbf{b}_1,...,\mathbf{b}_m c размерностью пространства n, записанных в матрице B с элементами \beta_{ij}.
Определим оператор проекции (проецирует вектор \mathbf{a} коллинеарно вектору \mathbf{b}) \mathbf{proj_b a = \frac{\left \langle a,b \right \rangle}{\left \langle b,b \right \rangle }b}, где \mathbf{\left \langle a,b \right \rangle} ― скалярное произведение векторов \mathbf{a} и \mathbf{b}.
Тогда ортогональные векторы вычисляются следующим образом:
\mathbf{b}_1 = \mathbf{a}_1
\mathbf{b}_2 = \mathbf{a}_2 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_2
\mathbf{b}_3 = \mathbf{a}_3 - \mathbf{proj}_{\mathbf{b}_1} \mathbf{a}_3 - \mathbf{proj}_{\mathbf{b}_2} \mathbf{a}_3
\vdots
\mathbf{b}_m = \mathbf{a}_m - \sum_{j=1}^{m-1} \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_m
Или поэлементно:
\beta_{1j} = \alpha_{1j}
\beta_{ij} = \alpha_{ij} - (\sum_{k=1}^{i-1} \mathbf{proj}_{\mathbf{b}_k} \mathbf{a}_i)_j = \alpha_{ij} - \sum_{k=1}^{i-1}\frac{\sum_{s=1}^{n}\alpha_{is}\beta_{ks}}{\sum_{s=1}^{n}\beta_{ks}\beta_{ks}}\beta_{kj}
1.3 Вычислительное ядро алгоритма
Основное время работы алгоритма приходится на вычисление сумм \sum_{i=1}^{j-1} \mathbf{proj}_{\mathbf{b}_i} \mathbf{a}_k \forall j: j=\overline{1, m}.
1.4 Макроструктура алгоритма
Из математического описания алгоритма и описания ядра алгоритма в предыдущих разделах следует, что основную часть данного метода составляют операции вычисления проекций векторов, а также их сумм. Таким образом, в алгоритме можно выделить следующие макрооперации: скалярное произведение векторов в количестве (m-1)m, а также множественные (всего m-1) вычисления сумм \mathbf{a}_i - \sum_{j=1}^{i-1} \frac{\left \langle a_i,b_j \right \rangle}{\left \langle b_j,b_j \right \rangle }b_j.
Макроструктура может быть представлена в следующем виде:
- Вычисление проекций \mathbf{proj}_{\mathbf{b}_j} \mathbf{a}_i \forall j: j=\overline{1, i - 1} для текущего шага i.
- Вычисление суммы \mathbf{a}_i - \sum_{j=1}^{i-1} \frac{\left \langle a_i,b_j \right \rangle}{\left \langle b_j,b_j \right \rangle }b_j для текущего шага i.
- Переход на следующий шаг.
1.5 Схема реализации последовательного алгоритма
Рассмотрим алгоритм, написанный в виде функции для математической системы MATLAB.
Входные данные.
Матрица A с линейно-независимыми векторами в столбцах.
Выходные данные.
Матрица Q с ортонормированным базисом A.
Использование.
Q = gramschmidt( A );
Реализация.
function Q = gramschmidt( A )
% Число векторов.
n = size( A, 2 );
% Инициализируем выходную матрицу.
Q = zeros( n );
% Преобразуем каждый вектор в базисный:
% (1) j-ый базисный вектор будет ортогонален каждому из предыдущих 1..j-1 векторов;
% (2) будет единичной длины.
for j = 1 : n
% Выбираем j-ый вектор
u = A( :, j );
% Специальный случай для j = 1: просто нормируем этот вектор и помещаем
% первым в найденный базис, так как нет векторов, относительно которых
% нужно было бы делать его ортогональным.
% Удаляем из оригинального вектора "u" все компоненты натянутые на базис
% из векторов 1..j-1, их вклад будет удален.
% => j-ый вектор ортогонален остальным.
% Предыдущие базисные вектора были найдены на предыдуших шагах.
% => соблюдаем принцип ортогональности, но не ортонормированности.
for i = 1 : j - 1
u = u - proj( Q(:,i), A(:,j) );
end
% Нормируем вектор
Q(:,j) = u ./ norm( u );
end
end
% Проекция вектора "a" коллинеарно вектору "e".
function p = proj( e, a )
p = (e' * a) / (e' * e) .* e;
end
1.6 Последовательная сложность алгоритма
Рассмотрим m векторов длины n.
- Скалярное произведение векторов требует n-1 сложение и n произведений.
- Вычитание проекции вектора требует 2 скалярных произведения, 1 деление, n произведений и n сложений, то есть:
- 3n-2 (+);
- 3n (\times);
- 1 (\div).
- Вычисление i-го вектора требует i-1 вычитаний проекций, то есть:
- (3n-2)(i-1) (+);
- 3n(i-1) (\times);
- i-1 (\div).
- Мы вычисляем вектора от i=1 до m, поэтому множители (i-1) выражаются треугольным числом (m-1)\frac{m}{2}.
- (3n-2)(m-1)\frac{m}{2} (+);
- 3n(m-1)\frac{m}{2} (\times);
- (m-1)\frac{m}{2} (\div).
Таким образом, cложность алгоритма O(nm^2).
1.7 Информационный граф
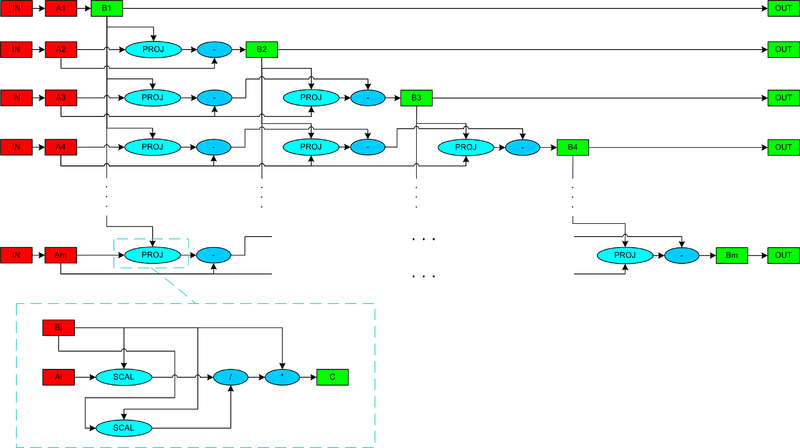
Граф состоит из элементов 2 видов: прямоугольников и овалов. Прямоугольниками обозначаются данные, причем красному цвету соответствуют входные данные, а зеленому ― выходные. Овалы означают операции над переданными данными. Голубым цветом обозначены более сложно организованные операции, а синим ― менее. Для нахождения \mathbf{b}_i вектора требуются значения всех векторов с номерами, меньшими i, однако, расчеты проекций можно начинать, не дожидаясь вычисления всех векторов, а производить сразу, как только соответствующий ортогональный вектор будет рассчитан. Эта зависимость и отражена на графе ниже.
1.8 Ресурс параллелизма алгоритма
Для построения базиса методом Грама–Шмидта в параллельном случае, имея в распоряжении m и более потоков, необходимо выполнить следующие ярусы:
- m-1 ярус вычисления проекций;
- m-1 ярус вычитания векторов.
Эти ярусы чередуются. Количество операций проекции и вычитания векторов уменьшается на единицу в каждом следующем ярусе. Вычисление проекции вектора требует 2 скалярных произведения, 1 деление и n произведений, то есть:
- 2n-2 (+);
- 3n (\times);
- 1 (\div).
Если считать, что вычисление проекции происходит последовательно, то сложность по высоте O(n), по ширине O(1) (то есть одна операция проекции в ярусе представляется набором ярусов с простыми последовательными операциями). В самом первом ярусе находится m-1 проекций и это наибольшее количество операций проекций, тогда сложность по высоте будет O(n), по ширине ― O(m).
Вычисление вычитания векторов требует n вычитаний, и если считать, что операция происходит последовательно, то сложность по высоте O(n), по ширине O(1). Во втором ярусе находится m-1 вычитаний и это наибольшее количество операций вычитаний, тогда сложность по высоте будет O(n), по ширине ― O(m).
Из вышеизложенного следует, что при классификации по ширине ЯПФ алгоритм имеет сложность O(m), а по высоте ― O(nm).
1.9 Входные и выходные данные алгоритма
Входные данные. Матрица A с элементами \alpha_{ij}, где i = \overline{1, m} (количество линейно независимых векторов) и j = \overline{1, n} (размерность пространства), при этом m \leqslant n.
Объем входных данных. mn
Выходные данные. Матрица B с элементами \beta_{ij}, где i = \overline{1, m} и j = \overline{1, n}, тогда b_{1}, \dots, b_{m} — система ортогональных векторов.
Объем выходных данных. mn
1.10 Свойства алгоритма
- Отношение последовательной и параллельной сложности в предположении доступности неограниченного числа необходимых ресурсов — m. При этом необходимо отметить, что отношение числа операций к суммарному объему входных и выходных данных (вычислительная мощность алгоритма) — линейное.
- Алгоритм почти полностью детерминирован, то есть гарантирована единственность результата выполнения. Это означает, что возможно накопление ошибок округления, то есть векторы выходной матрицы часто не точно ортогональны. Из-за потери ортогональности в процессе вычислений классический процесс Грама-Шмидта называют численно неустойчивым. Однако, процесс Грама-Шмидта может быть сделан более вычислительно устойчивым путём небольшой модификации. Такой алгоритм называется модифицированным процессом Грама-Шмидта. Рассмотрим его отличие подробнее.
\begin{array}{l} \mathbf{b}_j\\ \\ \mathbf{b}_j \end{array} \begin{array}{c} = \\ \\ = \end{array} \underbrace{ \underbrace{ \underbrace{ \begin{array}{c} \mathbf{a}_j \\ \\ \mathbf{a}_j \end{array} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_1}\,\mathbf{a}_j \end{array} }_{\mathbf{a}_j^{(1)}} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_2}\,\mathbf{a}_j^{(1)} \end{array} }_{\mathbf{a}_j^{(2)}} \begin{array}{c} - \\ \\ - \end{array} \begin{array}{c} \mathbf{proj}_{\mathbf{b}_3}\,\mathbf{a}_j \\ || \\ \mathbf{proj}_{\mathbf{b}_3}\,\mathbf{a}_j^{(2)} \end{array} }_{\mathbf{a}_j^{(3)}} \begin{array}{ccc} - & \ldots & - \\ \\ - & \ldots & - \end{array} \begin{array}{cc} \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j & (1) \\ || & \\ \mathbf{proj}_{\mathbf{b}_{j-1}}\,\mathbf{a}_j^{(j-2)} & (2) \end{array}
Формула (1) показывает вычисление \mathbf{b}_j в классическом процессе, а формула (2) — в модифицированном.
Разница между ними заключается в том, от каких векторов вычисляются компоненты: от \mathbf{a}_j в классическом процессе или от результата предыдущего вычитания, то есть от \mathbf{a}_j^{(k)} в модифицированном процессе. Таким образом, \mathbf{a}_j^{(k)} представляет собой \mathbf{a}_j, из которого удалены компоненты в направлениях \mathbf{b}_1,\,\;\ldots,\;\mathbf{b}_{k}. Компонента вектора \mathbf{a}_j в направлении \mathbf{b}_{k+1} при этом удалении не затрагивается и поэтому она в \mathbf{a}_j^{(k)} такая же, как в \mathbf{a}_j. - Процесс Грама-Шмидта может применяться к бесконечной последовательности линейно независимых векторов, а также к линейно зависимым векторам. В этом случае он выдаёт \mathbf{0} (нулевой вектор) на шаге j, если \mathbf{a}_j является линейной комбинацией векторов \mathbf{a}_1,\;\ldots,\;\mathbf{a}_{j-1}. Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые векторы и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (то есть количеству линейно независимых векторов, которые можно выделить среди исходных векторов).
- Процесс Грама-Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами — QR-разложение.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
В рамках статьи была написана своя параллельная реализация процесса ортогонализации Грама-Шмидта с использованием OpenMPI. Реализация вместе с данными и вспомогательными скриптами доступна в репозитории GramSchmidt.
Основная идея реализации: нулевой вычислительный узел является управляющим, остальные ― подчиненными. Подчиненные узлы запрашивают "задание" у управляющего узла ― номер вектора, который требуется расчитать. Когда подчиненный узел заканчивает расчет, то пересылает готовый вектор на управляющий узел и запрашивает следующее задание. Если заданий больше нет, то подчиненный узел заканчивает свою работу. Каждый узел имеет список уже готовых векторов. Если при расчете требуется вектор, которого нет в списке, то он запрашивается у управляющего узла.
Испытания реализованного алгоритма проводились на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета со следующими значениями параметров:
- размер матрицы по одному измерению: 100, 500 и далее с шагом 500 до 10000 элементов,
- число процессов: 1, 2, 4, 8 и далее с шагом 8 до 128. Тестирование с использованием 1, 2, 4 и 8 процессов не использовалось для данных, где размер превышал 5000.
Основная идея тестирования: для тестирования реализованного алгоритма были написаны генератор единичной матрицы и программа, проверяющая, что в поданном файле содержится корректная единичная матрица. Также для тестирования на "Ломоносове" был написан скрипт постановки задачи в очередь, поддерживающий в ней всегда три задачи с различными входными данными, то есть после завершения тестирования на одном наборе данных скрипт сразу же ставил в очередь очередной набор.
| развернутьИспользованные модули и компиляторы |
|---|
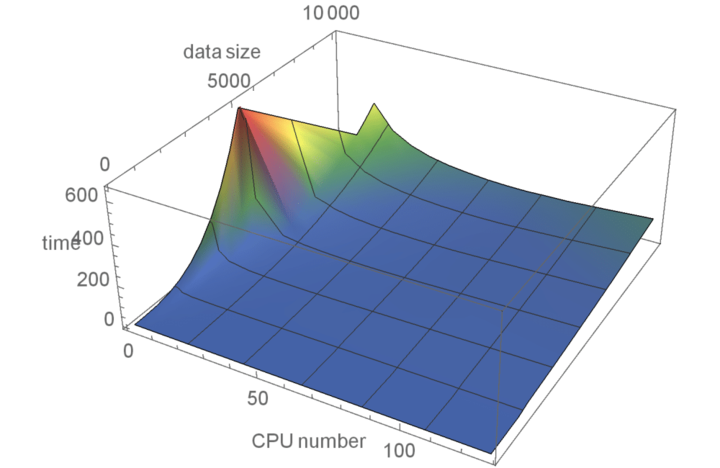
На следующем рисунке приведен график времени работы алгоритма в зависимости от числа процессов и размерности матриц.
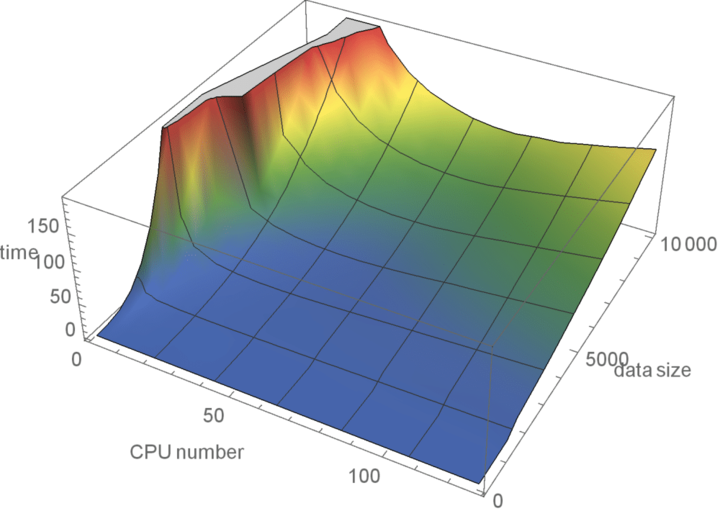
На следующем рисунке приведен график времени работы алгоритма в зависимости от числа процессов и размерности матриц, при этом часть данных с самым долгим временем работы отброшена, чтобы более наглядно продемонстрировать зависимость.
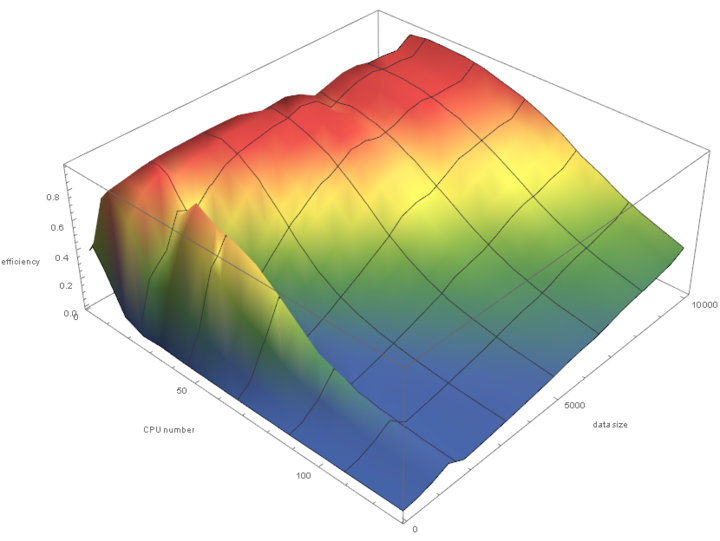
На следующем рисунке приведен график эффективности распараллеливания алгоритма в зависимости от числа процессов и размерности матриц.
Минимальная эффективность распараллеливания 0.12%. Максимальная ― 95%.
| Размер матрицы | 100 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 | 6500 | 7000 | 7500 | 8000 | 8500 | 9000 | 9500 | 10000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Число узлов, на которых время работы минимально | 1 | 32 | 48 | 56 | 24 | 32 | 32 | 40 | 40 | 40 | 48 | 56 | 56 | 56 | 64 | 64 | 72 | 72 | 72 | 80 | 80 |
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Данный алгоритм реализован во множестве библиотек и математических программных пакетах.
- Библиотека Epicycle (C#).
- Библиотека Spectral Python (SPy).
- Библиотека vect (Haskell).
2.7.1 Пакет Mathematica
Приведем пример скрипта, предназначенного для пакета Mathematica, который проводит процесс ортогонализации Грама-Шмидта над векторами, заданными в фигурных скобках последней строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты векторы \{-2,\;1,\;0\}, \{-2,\;0,\;1\}, \{-0{.}5,\;-1,\;1\}.
Projection[v1_, v2_] := (v1.v2*v2)/v2.v2
MultipleProjection[v1_, vecs_] := Plus @@ (Projection[v1, #1] &) /@ vecs
GramSchmidt[mat_] := Fold[Join[#1, {#2 - MultipleProjection[#2, #1]}] &, {}, mat]
GramSchmidt[{{-2, 1, 0}, {-2, 0, 1}, {-0.5, -1, 1}}]
2.7.2 Пакет Maxima
Приведем пример скрипта, предназначенного для пакета Maxima, который проводит процесс ортогонализации Грама-Шмидта над векторами, заданными в фигурных скобках последней строки. Количество векторов и их координат могут быть произвольными. В данном случае для примера взяты векторы \{-2,\;1,\;0\}, \{-2,\;0,\;1\}, \{-0{.}5,\;-1,\;1\}.
load(eigen);
x: matrix ([-2,1,0],[-2,0,1],[-0.5,-1,1]);
y: gramschmidt(x);2.7.3 Пакет MATLAB
Приведем пример скрипта, предназначенного для пакета MATLAB, который проводит процесс ортогонализации Грама-Шмидта над векторами, заданными в фигурных скобках последней строки. В данном пакете уже существует функция, которая осуществляет данный процесс. Столбцы входной матрицы предполагаются линейно-независимыми, количество векторов и их координат могут быть произвольными. Функция возращает матрицу X с ортонормированными столбцами и обратимую верхне-треугольную матрицу Y.
В данном случае для примера взяты векторы \{-2,\;1,\;0\}, \{-2,\;0,\;1\}, \{-0{.}5,\;-1,\;1\}.
[x y]=gschmidt([-2 1 0; -2 0 1; -0.5 -1 1])
3 Литература
- ↑ Канатников А.Н., Крищенко А.П. Линейная алгебра. ― 3-е изд., стер. ― М.: Изд-во МГТУ им. Н.Э. Баумана, 2002
- ↑ O'Connor, John J., Robertson, Edmund F. Jørgen Pedersen Gram ― MacTutor History of Mathematics archive, University of St Andrews.
- ↑ O'Connor, John J., Robertson, Edmund F. Erhard Schmidt ― MacTutor History of Mathematics archive, University of St Andrews.
- ↑ Орешкин Б.Н., Бакулев П.А. Быстрая процедура ортогонализации Грамма-Шмидта и ее применение для борьбы с помехами в адаптивной системе селекции движущихся целей ― Радиотехника / №12 за 2007 г.
- ↑ Пискова А.В., Менщиков А.А., Коробейников А.Г. Использование ортогонализации Грама-Шмидта в алгоритме приведения базиса решетки для протоколов безопасности ― Вопросы кибербезопасности №1(14) 2016
- ↑ Карелин А.Е., Светлаков А.А. Использование ортогонализации Грама-Шмидта для повышения экономичности многоточечных алгоритмов рекуррентного оценивания параметров моделей объектов управления ― Известия Томского политехнического университета [Известия ТПУ]. — 2006. — Т. 309, № 8. — [С. 15-19].