Адаптивное интегрирование: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Bvdmitri (обсуждение | вклад) |
|||
| Строка 11: | Строка 11: | ||
Формулы метода: | Формулы метода: | ||
| − | # | + | # Интеграл функции вычисляется по квадратурной [https://ru.wikipedia.org/wiki/Формула_Симпсона формуле Симпсона] с числом узловых точек равным 4 и 8 на отрезке [a, b]. |
| − | # | + | # Вычисляется разность найденных значений |
| − | ## Если разность | + | ## Если разность интегралов меньше либо равна желаемой точности интегрирования ε - заканчиваем процедуру. |
| − | ## Если разность больше, то | + | ## Если разность больше, то отрезок разбивается на два [a, (a + b) / 2] и [(a + b) / 2, b] и для каждого отрезка повторяется процедура 1, затем возвращается сумма полученных значений. |
Из описания видно, что алгоритм имеет рекурсивную природу. | Из описания видно, что алгоритм имеет рекурсивную природу. | ||
Версия 00:04, 14 ноября 2016
Незаконченный вариант статьи
Содержание
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Адаптивное интегрирование - метод быстрого вычисления интеграла функции, который использует адаптивное изменение плотности сетки интегрирования. На промежутках, где функция гладкая, сетка разреженная, на промежутках со значительными колебаниями значений сетка гуще для получения необходимой точности.
1.2 Математическое описание алгоритма
Формулы метода:
- Интеграл функции вычисляется по квадратурной формуле Симпсона с числом узловых точек равным 4 и 8 на отрезке [a, b].
- Вычисляется разность найденных значений
- Если разность интегралов меньше либо равна желаемой точности интегрирования ε - заканчиваем процедуру.
- Если разность больше, то отрезок разбивается на два [a, (a + b) / 2] и [(a + b) / 2, b] и для каждого отрезка повторяется процедура 1, затем возвращается сумма полученных значений.
Из описания видно, что алгоритм имеет рекурсивную природу.
1.3 Макростуктура алгоритма
Основную часть метода составляют рекурсивные вызовы интегралов отрезков меньшей длинны.
1.4 Входные данные
- Функция.
- Отрезок вида [a, b].
- Желаемая точность интегрирования ε.
1.5 Выходные данные
- Интеграл функции на отрезке [a, b] с точностью ε.
2 Программная реализация алгоритма
2.1 Исходный код реализованного алгоритма
Весь исходный код в статье можно найти в репозитории на GitHub.
2.2 Реализации на одном процессоре
Простейшую рекурсивную реализацию данного алгоритма , которая не использует ресурсы параллелизма можно посмотреть здесь.
#include "SequentialMethod.h"
SequentialMethod::SequentialMethod(double eps, const std::function<double(double)> &f) : IntegrationMethod(eps, f) {}
double SequentialMethod::integrate(double a, double b) {
double x = simpson(a, b, 4);
double y = simpson(a, b, 8);
if (fabs(x - y) < eps) {
return y;
} else {
return integrate(a, (a + b) / 2.0) + integrate((a + b) / 2.0, b);
}
}
SequentialMethod::~SequentialMethod() {}
Реализация с помощью библиотеки Intel TBB для более эффективного использования многоядерных процессоров можно посмотреть здесь.
#include "TBBMethod.h"
TBBMethod::TBBMethod(double eps, const std::function<double(double)> &f) : IntegrationMethod(eps, f) {}
double TBBMethod::integrate(double a, double b) {
double x = simpson(a, b, 4);
double y = simpson(a, b, 8);
if (fabs(x - y) < eps) {
return y;
} else {
tbb::task_group group;
group.run([&] {
x = integrate(a, (a + b) / 2.0);
});
group.run_and_wait([&] {
y = integrate((a + b) / 2.0, b);
});
return x + y;
}
}
TBBMethod::~TBBMethod() {}
2.3 Параллельная реализации
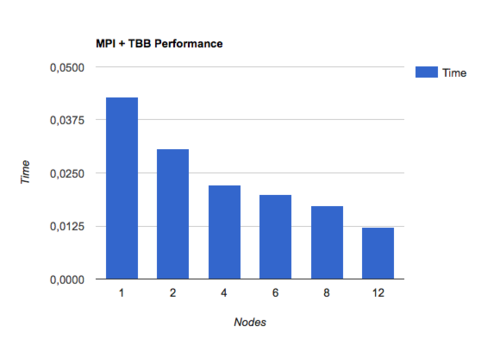
2.3.1 Реализация с помощью MPI для межпроцессорного взаимодействия и Intel TBB для внутрипроцессорного взаимодействия
В данной реализации отрезок [a, b] делится на число доступных процессоров, каждый отрезок считается на своем процессоре, рекурсия заменяется на систему задач библиотеки Intel MPI для более эффективного использования многоядерных процессоров.
2.3.2 Реализация только с помощью MPI
В данной реализации рекурсия заменяется на систему задач, каждая задача представляет собой подсчет интеграла на отрезке, в случае если необходимая точность не достигнута (см. Математическое описание алгоритма), создаются две новые задачи с меньшими отрезками и распределяются между другими процессорами. Данная реализация в теории решает проблему неравномерности гладких и не гладких участков функции, в случае когда большая часть участков гладкая и лишь небольшой участок функции сильно осциллирует.