Уровень алгоритма

Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
[непроверенная версия][непроверенная версия]
 
(не показано 35 промежуточных версий 1 участника)
Строка 1: Строка 1:
−
Авторы: Абдулпотиев А.А.
+
Автор: Абдулпотиев А.А.
  
−
== Свойства и структура алгоритма ==
+
{{algorithm
−
===Общее описание алгоритма===
+
| name              = Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией
−
Алгоритм Лáнцоша является мощным инструментом для решения некоторого класса больших разреженных симметричных спектральных задач <math> A x = λ x</math>. Однако любая практическая реализация этого алгоритма страдает от ошибок округления, т.к. векторы Ланцоша теряют взаимную ортогональность. Для того чтобы поддерживать некоторый уровень ортогональности, появились методы полной переортогонализации и выборочной ортогонализации. В этой работе мы рассмотрим последний метод в качестве способа для поддержания ортогональности среди векторов Ланцоша. Он обладает почти столь же высокой точностью, как алгоритм с полной переортогонализацией, и почти столь же низкой стоимостью, как алгоритм без ортогонализации <ref>"The Lanczos Algorithm With Partial Reorthogonalization", Horst D. Simon, Mathematics of computation, volume 42, number 165, pages 115-142  (1984)</ref>.
+
| serial_complexity = <math>O(kn^2 + k^2n)</math>
 +
| pf_height        = <math>O(kn + k^2)</math>
 +
| pf_width          = <math>O(n)</math>
 +
| input_data        = <math>{n (n + 1) \over 2} + n + 1</math>
 +
| output_data      = <math>k + nk</math>
 +
}}
  
 +
= Свойства и структура алгоритма =
 +
== Общее описание алгоритма ==
  
−
Дается вещественная симметричная матрица  <math>A = A^T</math>,
+
Алгоритм Ланцоша это итерационный метод нахождения небольшого количества собственных значений столь больших разреженных симметричных матриц, что к ним нельзя применить прямые методы. Иными словами алгоритм сильно оптимизирует использование памяти и вычислительной мощности, что является критически важным для больших вычислений.  
−
{{Шаблон:ASymmetric}} <math> \, \;  (1), </math>
 
−
случайный вектор <math>b </math>, являющийся первым приближением собственного вектора матрицы, <math>k </math> - количество собственных значений и собственных векторов, которые мы хотим найти, т.е. количество итераций.
 
  
 +
Сам алгоритм объединяет метод Ланцоша для построения крыловского подпространства с процедурой Рэлея-Ритца интерпретации собственных значений некоторой вычисляемой матрицы как приближений к собственным значениям исходной матрицы.
  
−
На каждой итерации строится матрица <math>Q_j = [q_1, q_2, \dots, q_j]</math> размерности <math>n \times j</math>, состоящая из ортонормированных векторов Ланцоша <math>z</math>. В качестве приближенных собственных значений берутся числа Ритца <math>\theta_i </math>, т.е. собственные значения симметричной трехдиагональной матрицы <math>T_j = Q^T_j A Q_j</math> размерности <math>j \times j</math>.
+
Пусть <math>Q = [Q_k,Q_u]</math> - ортогональная матрица порядка <math>n</math>, причем <math>Q_k</math> и <math>Q_u</math> имеют соответственно размеры <math>n \times k</math> и <math>n \times (n-k)</math>. Столбцы матрицы <math>Q_k</math> вычисляются методом Ланцоша..
 +
 
 +
Запишем следующие соотношения:
 +
 
 +
<math>T = Q^T A Q = [Q_k, Q_u]^T A [Q_k, Q_u] =
 +
\left[ \begin{array}{cc}
 +
Q_k^T A Q_k & Q_k^T A Q_u\\
 +
Q_u^T A Q_k & Q_u^T A Q_u
 +
\end{array} \right]
 +
= \left[ \begin{array}{cc}
 +
T_{k} & T_{ku}^T\\
 +
T_{ku} & T_{u}
 +
\end{array} \right]</math>
 +
 
 +
Метод Рэлея-Ритца заключается в интерпретации собственных значений матрицы <math>T_k = Q_k^T A Q_k</math> как приближенных к собственным значениям матрицы <math>A</math>. Эти приближения называются числами Ритца. Если <math>A = V \Lambda V^T</math> есть спектральное разложение матрицы <math>T_k</math>, то столбцы матрицы <math>Q_k V</math> являются приближениями соответствующих собственных векторов и называются векторами Ритца.
 +
 
 +
Числа и векторы Ритца являются ''оптимальными'' приближениями к собственным значениям и собственным векторам матрицы <math>A</math>.
 +
 
 +
При применении метода Ланцоша в арифметике с плавающей точкой ортогональность в вычисленных векторах Ланцоша <math>q_k</math> пропадает из-за ошибок округления. Потеря ортогональности не заставляет алгоритм вести себя совершенно не предсказуемым образом. В самом деле, мы увидим, что цена, которую мы платим за потерю, это приобретение повторных копий сошедшихся чисел Ритца. Для того чтобы поддержать взаимную ортогональность векторов Ланцоша, существуют две модификации алгоритма.
 +
# '''Алгоритм Ланцоша с полной переортогонализацией'''. На каждой итерации запускается повторный процесс ортогонализации Грамма-Шмидта <math>z = z - \textstyle \sum_{i=1}^{j-1} (z^T q_i)q_i \displaystyle</math>  
 +
# '''Алгоритм Ланцоша с выборочной ортогонализацией'''. Согласно теореме Пейджа векторы <math>q_k</math> теряют ортогональность весьма систематическим образом, а именно, приобретая большие компоненты в направлениях уже сошедшихся векторов Ритца (Именно это приводит к появлению повторных копий сошедшихся чисел Ритца). Поэтому можно выборочно ортогонализировать векторы <math>q_k</math> вместо того, чтобы на каждом шаге ортогонализировать вектор ко всем ранее сошедшимся векторам, как это делается при полной ортогонализации. Таким образом достигается (почти) ортогональности векторов Ланцоша, затрачивая очень небольшая дополнительную работу.
 +
 
 +
== Математическое описание алгоритма ==
 +
 
 +
Пусть <math>A</math> - заданная симметричная матрица, <math>b</math> - вектор начального приближения метода Ланцоша.
 +
Тогда алгоритм Ланцоша вычисления собственных векторов и собственных значений матрицы <math>A</math> с выборочной ортогонализацией имеет следующий вид:
 +
 
 +
<math>
 +
\begin{align}
 +
q_1 = & b / \Vert b \Vert_2, \; \beta_0 = 0,\; q_0 = 0\\
 +
for \; & j = 1 \; to \; k \\
 +
& z = A\,q_j\\
 +
& \alpha_j = q_j^T z\\
 +
& z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}\\
 +
& for \; i=1 \; to \; k \\
 +
& \; \; \; if \; \beta_k \|v_i (k)\| \le \sqrt{\epsilon} \Vert T_k \Vert_2 \; then\\
 +
& \; \; \; \; \; \; z = z - (y_{i,k} ^ T z) y_{i,k} \;/*\; y_{i,k} = Q_k v_i \;*/ \\
 +
& end \; for\\
 +
& \beta_j = \Vert z \Vert_2\\
 +
& if \; \beta_j = 0 \; then\\
 +
& \; \; \; Stop\; the\; algorithm\\
 +
& q_{j+1} = z / \beta_j\\
 +
& /*Calculate\; eigenvalues\; and\; eigenvektors\; of\; T_j\; */\\
 +
end \; & for
 +
\end{align}
 +
</math>
 +
 
 +
Где <math>v_i</math> - это столбцы ортогональной матрицы <math>V</math> из спектрального разложения <math>T_k = V \Lambda V^T</math>, а <math>y_{k,i} = Q_k v_i</math> - столбцы матрицы <math>Q_k V</math> - векторы Ритца.
 +
 
 +
Матрица <math>T_j</math>
  
 
:<math>
 
:<math>
Строка 20: Строка 75:
 
& & \ddots & \ddots & \beta_{j-1} \\
 
& & \ddots & \ddots & \beta_{j-1} \\
 
& & & \beta_{j-1} & \alpha_j
 
& & & \beta_{j-1} & \alpha_j
−
\end{pmatrix}\; (2).
+
\end{pmatrix}\;
 
</math>
 
</math>
−
 
−
Однако, векторы <math>q_j </math> теряют ортогональность вследствие приобретения больших компонент в направлениях векторов Ритца <math>y_{i,j} = Q_j v_i </math>, отвечающих сошедшимся числам Ритца <math> \theta_i </math>. Поэтому чтобы построить <math>q_j </math>, предлагается на каждом шаге следить за оценками погрешностей  <math>\beta_{t}|v_i(t)|, i = 1 \dots t, t = j - 1 </math>, где <math>v_i(t) </math> - <math>t</math>-я компонента собственного вектора <math>v_i </math>. И когда какая-то оценка становится слишком малой, проводить ортогонализацию вектора Ланцоша <math>z </math>. Величина <math>\beta_{t}|v_i(t)| </math> считается малой, если она меньше, чем <math>\sqrt{\varepsilon}||T_{t}|| </math>, где <math>\varepsilon</math> - доступная машинная точность чисел.
 
  
  
−
После следует вычисление собственных значений  <math> \theta_j </math> и собственных векторов <math>v_j </math> полученной трехдиагональной матрицы <math>T_j</math>, для чего существует, например, метод "разделяй и властвуй"<ref>Дж. Деммель «Вычислительная линейная алгебра», c. 232, алгоритм 5.2</ref>
+
Согласно теореме Пейджа, <math>y_{k,i}^T q_{k+1} = O(\epsilon \Vert A \Vert_2) / \beta_k \Vert v_i(k) \Vert</math>, то есть компонента <math>y_{k,i}^T q_{k+1}</math> вычисленного вектора Ланцоша <math>q_{k+1}</math> в направлении вектора Ритца <math>y_{k,i} = Q_k v_i</math> обратно пропорциональна величине <math>\beta_k \Vert v_i(k) \Vert</math>, являющейся оценкой погрешности для соответствующего числа Ритца. Поэтому, когда число Ритца сходится, а его оценка погрешности приближается к нулю, вектор Ланцоша приобретает большую компоненту в направлении вектора Ритца <math>q_{k,i}</math>, и следует произвести процедуру переортогонализации.
  
−
=== Математическое описание алгоритма ===
+
Величина погрешности <math>\beta_k \Vert v_i(k) \Vert</math> считается малой, если она меньше, чем <math>\sqrt{\epsilon} \Vert A \Vert_2</math>, так как в этом случае, согласно теореме Пейджа, компонента <math>\Vert y_{i,k}^T q_{k+1} \Vert = \Vert y_{i,k}^T z \Vert / \Vert z \Vert_2</math> скорее всего превосходит уровень <math>\sqrt{\epsilon}</math> (на практике используется <math>\Vert T_k \Vert_2</math> вместо <math>\Vert A \Vert_2</math>, так как первое известно, а второе не всегда).
−
<math> \beta_0=0,q_0=0</math>
 
−
<math> q_{1} = \frac{b_{j}}{\|b\|_2}</math>, где <math> \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2}</math>
 
−
<math> for\, j=1\,\, to\, \, k\, \, do:</math>
 
−
    <math>z=Aq_j, </math>
 
−
    <math>\alpha_j=q_j^Tz, </math>
 
−
    <math>z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  </math>
 
−
    <math>t = j - 1,  </math>
 
−
    <math>for\, i=1\,\, to\, \, t\, \, do: </math>
 
−
        <math>if\,  \beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \,  then:</math>
 
−
            <math>z = z-(y^T_{i,t},z)y_{i,t} </math>, где <math>y_{i,t} = Q_{t}v_i</math>  
 
−
    <math>\beta_{j}=\|z\|_2 </math>
 
−
    <math>q_{j+1}=z/\beta_{j}, </math>
 
−
    Строим матрицу  <math> T_j</math> (2), вычисляем собственные значения  <math> \theta_j </math> и собственные векторы <math>v_j </math> полученной матрицы <math>T_j</math>.
 
  
−
=== Вычислительное ядро алгоритма ===
+
== Вычислительное ядро алгоритма ==
−
Выделены следующие вычислительные ядра:
 
  
−
* Умножение матрицы на вектор, <math>z=Aq_j,  </math>.
+
У описанного алгоритма два ядра, на которые приходится основное время работы алгоритма:
  
 +
* Вычисление вектора <math>z = A q_j</math>
 +
* Выборочная переортогонализация <math>z = z - (y_{i,k} ^ T z) y_{i,k}</math>
 +
При больших <math>k</math>, сопоставимых с <math>n</math> , к вычислительному ядру можно отнести вычисление собственных значений и собственных векторов трёхдиагональной матрицы. Однако на практике <math>k</math> много меньше <math>n</math>.
  
−
* Ортогонализация по отношению к сошедшимся векторам  <math>z = z-(y^T_{i,t},z)y_{i,t} </math> для <math>i  = 1 \dots t</math>
+
== Макроструктура алгоритма ==
  
 +
Макроструктура алгоритма Ланцоша с выборочной переортогонализацией представляется в виде совокупности метода Ланцоша с выборочной переортогонализацией построения крыловского подпространства и процедуры Рэлея-Ритца.
  
−
===Макроструктура алгоритма===
+
Каждая итерация первого этапа может быть разложена на следующие макроединицы:
−
Были выделены следующие макрооперации:
 
  
−
1. Умножение матрицы на вектор,  
+
1 Умножение матрицы на вектор, <math>z=Aq_j</math>.
−
 
 
−
<math>z=Aq_j,  </math>.  
 
  
 
2. Вычисление вектора <math>q_{j+1} </math> с помощью линейной комбинации других векторов:
 
2. Вычисление вектора <math>q_{j+1} </math> с помощью линейной комбинации других векторов:
Строка 69: Строка 109:
 
3. Ортогонализация вектора Ланцоша с помощью скалярного произведения:   
 
3. Ортогонализация вектора Ланцоша с помощью скалярного произведения:   
  
−
<math>z = z-(y^T_{i,t},z)y_{i,t} </math>
+
<math>z = z-(y^T_{i,k},z)y_{i,k} </math>
 +
 
 +
4. Нахождении собственных значений и собственных векторов матрицы и интерпретации их как приближенных значений собственных чисел и собственных векторов исходной матрицы, он может быть выполнен любым способом, например, разделяй и властвуй или же QR-итерацией.
 +
 
 +
== Схема реализации последовательного алгоритма ==
  
−
4. Для вычисления собственных значений матрицы будет использоваться алгоритм "разделяй и властвуй".
+
На вход алгоритму подаются исходная матрица <math>A</math>, вектор начального приближения <math>b</math> и число <math>k</math>.
 +
Далее последовательно выполняются итерационно для всех <math>j: 1 \le j \le k</math> следующие шаги:
  
−
===Схема реализации последовательного алгоритма===
+
# Умножается матрица на вектор для нахождения вектора <math>z</math>
 +
# Вычисляется коэффициент <math>\alpha_j</math> посредством скалярного перемножения векторов
 +
# Вычисляется новое значение вектора <math>z</math>
 +
# Производятся оценка погрешностей <math>\beta_k \Vert v_i(k) \Vert</math> и выборочная переортогонализация
 +
# Вычисление очередного значения <math>\beta_j</math> - норма вектора <math>z</math>
 +
# Вычисление и добавление к матрице <math>Q</math> нового столбца
 +
# Вычисление собственных значений и собственных векторов матрицы <math>T_j</math>
  
−
<math>1)</math> Инициализируются векторы <math> \beta_0=0,q_0=0,</math>
+
== Последовательная сложность алгоритма ==
−
<math>2)</math> Считается норма вектора <math> b: \; \;  \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2},</math>
 
−
<math>3)</math> Находится первый вектор матрицы <math> Q: \; \; q_{1} = \frac{b_{j}}{\|b\|_2},</math>
 
−
<math>4)</math> Начинается цикл, повторяющийся <math> k </math> раз по переменной <math> j: </math>
 
−
    <math>4.1)</math> Считается произведение матрицы на вектор: <math> z_d = \sum\limits_{y=1}^{n} a_{dy} q_{j_y}, \; d = 1,\,\dots\,, n, </math> где
 
−
    <math>z_d - </math> компоненты вектора Ланцоша <math>z, </math>
 
−
    <math>4.2)</math> Скалярно умножается <math>q_j^T</math>  и <math> z: \; \; \alpha_j = \sum\limits_{d=1}^{n}q_{j_d} z_d,</math>
 
−
    <math>4.3)</math> Вычисляется линейная комбинация векторов <math>z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  </math>
 
−
    <math>4.4)</math> <math>t</math> Присваивается <math>j - 1.  </math> В цикле по <math> i </math> от первого до посчитанного <math> t</math>-го собственного вектора проводится
 
−
    выборочная ортогонализация к сошедшимся векторам Ритца. То есть:
 
−
      <math>4.4.1)</math> Считается норма матрицы <math>\|T_{t}\|_2, </math> <math> \| T \|_2 =  \sup\limits_{\| x \|_2 = 1} \| T x \|_2 = \sup\limits_{(x, x) = 1} \sqrt{(Tx, Tx)}</math>, подчиненная векторной норме <math> \| x \|_2 = \sqrt{\sum_{i = 1}^n |x_i|^2} </math>. Т.е.
 
−
      <math> \|    T_{t} \|_2 =  \max\limits_{i=1 \dots t} \theta_i</math>, где <math> \theta_i</math> - собственные значения матрицы <math> T,</math>
 
−
      <math>4.4.2)</math> Берется <math>t</math>-ю координата вектора <math> v_i</math>  и проверяется, выполняется ли равенство:<math>\beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \, ,</math>
 
−
      Если выполняется, то
 
−
          <math>4.4.2.1)</math> Ищется вектор Ритца <math>y_{i,t_d} = \sum\limits_{x=1}^{t} q_{x_d} v_{i_x}, \; d = 1,\,\dots\,, n,</math>, где  <math>y_{i,t_d}</math> -  <math>d</math>-я компонента вектора Ритца <math>y,</math>
 
−
          <math>4.4.2.2)</math> Скалярно умножается <math>y_{i,t}^T</math>  и <math> z: \; \; \gamma = \sum\limits_{d=1}^{n}y_{i,t_d} z_d,</math>
 
−
          <math>4.4.2.3)</math> Вычисляется линейная комбинация векторов <math>z = z-\gamma\,  y_{i,t}, </math>
 
−
          <math>4.4.2.4)</math> Увеличивается <math>i </math>. Производится возврат к пункту <math>4.4.2,</math>
 
−
    <math>4.5)</math> Ищется норма вектора <math> z: \; \; \beta_{j}=\|z\|_2, </math>
 
−
    <math>4.6)</math> Ищется вектор Ланцоша <math>q_{j+1}=z/\beta_{j}, </math>
 
−
    <math>4.7)</math> Вычисляется новое собственное значение <math> \theta_j </math> и собственный вектор <math> v_j </math> для полученной матрицы <math> T_j,</math>
 
−
    <math>4.8)</math> Увеличивается <math> j </math>, производится возврат к шагу <math>4.1.</math>
 
  
−
===Последовательная сложность алгоритма===
+
* Вычисление вектора <math>z</math> - <math>n^2</math> операций умножения и <math>n(n-1)</math> операций сложения
−
Рассмотрим последовательную сложность алгоритма.
+
* Вычисление скалярного произведения векторов - <math>n</math> операций умножения и <math>(n-1)</math> сложений
−
<math>1)</math> Инициализируются векторы,
+
* Вычисление вектора <math>z</math> - <math>2n</math> умножений и <math>2n</math> сложений
−
<math>2)</math> Считается норма вектора: <math> n </math> сложений и умножений, одно вычисление корня,
+
* Оценка погрешностей - <math>kn</math> операций умножения
−
<math>3)</math> Находится первый вектор матрицы: <math> n </math> делений,
+
* Выборочная переортогонализация - <math>O(2nj)</math> умножений и <math>O(2j(n-1) + n)</math> сложений
−
<math>4)</math> Начинается цикл, повторяющийся <math> k </math> раз по переменной : <math>  j </math>:
+
* Вычисление нормы вектора - <math>n</math> операций умножения и <math>(n-1)</math> сложений
−
    <math>4.1)</math> Считается произведение матрицы на вектор: <math>  n </math> сложений и умножений,
+
* Вычисление нового столбца матрицы <math>Q</math> - <math>n</math> операций умножения
−
    <math>4.2)</math> Скалярно умножается два вектора : <math>  n </math> сложений и умножений,
 
−
    <math>4.3)</math> Вычисляется линейная комбинация векторов : <math>  2n </math> вычитаний и умножений,
 
−
    <math>4.4)</math> Повторяется цикл : <math>  j-1 </math> раз. На каждом из этапов:
 
−
      <math>4.4.1)</math> Считается норма матрицы: : <math>  j-1 </math> сравнений,
 
−
      <math>4.4.2)</math> Проверяется равенство::  2 умножения, одно сравнение
 
−
          <math>4.4.2.1)</math> Ищется вектор Ритца : <math>  n*(j-1) </math> сложений и умножений,
 
−
          <math>4.4.2.2)</math> Скалярно умножаются два вектора:  <math>   n </math> сложений и умножений,
 
−
          <math>4.4.2.3)</math> Вычисляется линейная комбинация векторов : <math>  n </math> умножений и вычитаний,
 
−
          <math>4.4.2.4)</math> Увеличивается <math>i </math>. Одно сложение.
 
−
      Таким образом, т.к. внутренний цикл повторяется <math>  j-1 </math> раз, а <math>  j </math> в свою очередь пробегает от <math>1 \dots k </math>, значит, полное количество операций в пункте <math>4.4)</math>, которое будет занимать весь внутренний цикл будет: сравнений <math> \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} </math>, умножений: <math> 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} </math>, сложений <math>\frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}</math> и вычитаний <math> \frac{(n)k(k-1)}{2}</math>
 
−
    <math>4.5)</math> Ищется норма вектора: <math> n </math> сложений и умножений
 
−
    <math>4.6)</math> Ищется вектор Ланцоша <math> n </math> делений
 
−
    <math>4.7)</math> Увеличивается <math> j </math>, одно сложение.
 
−
   
 
−
    Так, пункты  <math>4.1 - 4.3, 4.5 - 4.7</math> занимают <math> k*(n+n+n+1)</math> сложений, <math>k(n+n+2n+n)</math> умножений, <math>2nk</math> вычитаний и <math>n</math> делений.
 
−
 
−
 
−
 
−
Подводя итог, общее количество операций умножения и деления <math>n + n + 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} +  k(n+n+2n+n) + n</math>, т.е. <math>O( k^3+nk^2+k^2+kn+n )</math>
 
−
общее количество сложений и вычитаний: <math> n + \frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}+ \frac{(n)k(k-1)}{2} + k*(n+n+n+1) + 2nk</math>, т.е.  <math>O( k^3+nk^2+kn+n )</math>
 
−
И <math> \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} </math> сравнений ( <math>O( k^3+k^2)</math>).
 
  
 +
Итого на каждой итерации:
  
 +
* Умножений: <math>n^2 + n + 2n + kn + O(2nj) + n + n = n^2 + 5n + kn + O(2nj)</math>
 +
* Сложений: <math>n(n-1) + n-1 + 2n + O(2j(n-1) + n) + n-1 = n^2 + 3n + O(2j(n-1) + n) -2</math>
  
−
[[File:Graph.jpg|200px|right| frame |рис. 1: Информационный граф]]
+
Итого за все время выполнения алгоритма:
  
−
=== Информационный граф===
+
* Умножений: <math>kn^2 + 5kn + k^2n + O(k^2n + kn)</math>
−
На рисунке (рис. 1) изображен информационный граф. Ниже приведено его описание:
+
* Сложений: <math>kn^2 + 3kn + O((k^2+k)(n-1)+kn) = kn^2 + 3kn + O(k^2(n-1)+2kn-k)</math>
  
−
* Вершины 1 соответствуют операции  <math>Aq_j,</math>.
+
Суммарная последовательная сложность алгоритма - <math>O(kn^2 + k^2n)</math>.
−
* Вершины 2 соответствуют операции скалярного произведения <math>q_j^Tz</math>.
 
−
* Вершины 3 соответствуют операции <math>z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i</math>.
 
−
* Вершины 4 соответствуют операции <math>z-\alpha_jq_j-\beta_{j-1}q_{j-1}</math>.
 
−
* Вершины 5 соответствуют операции <math>||z||</math>.
 
−
* Вершины 6 соответствуют операции <math>z/\beta_j</math>.
 
  
−
=== Ресурс параллелизма алгоритма===
+
== Информационный граф ==
 +
[[Файл:Lancos_SO_ingrpah.png|center|frame |рис. 1: Информационный граф]]
  
−
Хотя алгоритм является итерационным, возможно распараллелить внутри каждой итерации умножение матрицы на вектор и процесс переортогонализации Грамма-Шмидта.
+
== Ресурс параллелизма алгоритма ==
  
−
Процесс умножения матриц matvec можно распараллелить несколькими способами[https://eprint.iacr.org/2011/416.pdf].
+
Поскольку алгоритм является итерационным, то выполнять параллельные операции возможно только внутри каждой итерации алгоритма. Сами итерации выполняются в строгой последовательности и не могут быть параллелизованны:
  
−
Как видно из графа, для выполнения j-й операции, необходимо выполнить следующие ярусы:
+
* Вычисление вектора <math>z</math> - умножение матрицы размера <math>n \times n</math> на вектор длины <math>n</math> - <math>n</math> ярусов сложений, <math>n</math> операций умножений в каждом
−
# <math>n</math> ярусов сложений с <math>n</math> операциями умножения в каждом (вычисление <math>z</math>);
+
* Вычисление коэффициента <math>\alpha_j</math> - скалярное произведение векторов - <math>n</math> ярусов сложений, 1 операция умножения в каждом
−
# <math>n</math> ярусов сложений с <math>1</math> операцией умножения в каждом (вычисление <math>\alpha_j</math>);
+
* Вычисление нового значения вектора <math>z</math>: 2 яруса умножений длины <math>n</math> (умножение вектора на число), 2 яруса вычитаний длины <math>n</math>
−
# <math>j</math> ярусов сложений с <math>n</math> операциями умножения в каждом, <math>n</math> ярусов сложений с <math>j</math> операциями умножения в каждом, <math>1</math> ярус вычитаний размера <math>n</math> (первая переортогонализация);
+
* Выборочная переортогонализация: последовательно для всех <math>i \le k</math> выполняется <math>j</math> ярусов сложений, <math>n</math> операций умножений в каждом, <math>n</math> ярусов сложений, <math>j</math> операций умножений в каждом, один ярус вычитаний размера <math>n</math>
−
# <math>j</math> ярусов сложений с <math>n</math> операциями умножения в каждом, <math>n</math> ярусов сложений с <math>j</math> операциями умножения в каждом, <math>1</math> ярус вычитаний размера <math>n</math> (вторая переортогонализация);
+
* Вычисление <math>\beta_j</math> - скалярное произведение векторов - <math>n</math> ярусов сложений, 1 операция умножения в каждом
−
# <math>n</math> ярусов сложений с <math>1</math> операцией умножения в каждом (вычисление <math>\beta_j</math>);
+
* Вычисление <math>q_j</math> - деление вектора на число - один ярус делений размера <math>n</math>
−
# <math>1</math> ярус делений размера <math>n</math> (вычисление <math>q_{j + 1}</math>).
 
  
−
Если учесть весь ресурс параллелизма, можно получить мультипликативную вычислительную сложность всего алгоритма: <math>O(n^2k+nk^2)/p)</math>.
+
Сложность алгоритма по ширине ярусно параллельной формы  - <math>O(n)</math>.
  
−
Вычислительная мощность данного алгоритма, как отношение числа операций к суммарному объему входных и выходных, данных равняется  <math>O(k)</math>.
+
== Входные и выходные данные алгоритма ==
  
−
=== Входные и выходные данные алгоритма===
 
 
'''Входные данные'''
 
'''Входные данные'''
  
−
Матрица  <math> A </math>, начальный вектор <math> b </math> и число собственных значений, которые мы хотим найти  <math> k </math>.
+
Вещественная матрица <math>A</math> размера <math>n \times n</math>, вектор <math>b</math> длины <math>n</math>, число <math>k</math>, но учитывая что матрица у нас симметричная количество входных данных можно уменьшить в два раза.
  
−
Ввиду симметричности из матрицы <math> A </math> достаточно хранить только ее диагональ и элементы, лежащие выше ее. Таким образом, объем входных данных:  
+
Объем входных данных: <math>{n (n + 1) \over 2} + n + 1</math>
−
 
 
−
<math>\frac{n (n + 1)}{2} + n + 1 = \frac{n^2+3n+2}{2}.</math>
 
  
 
'''Выходные данные'''
 
'''Выходные данные'''
Строка 174: Строка 178:
 
Так, объем выходных данных:  <math> k + kn </math>
 
Так, объем выходных данных:  <math> k + kn </math>
  
−
=== Свойства алгоритма ===
+
== Свойства алгоритма ==
−
Если <math>A</math> эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам Ритца[http://ta.twi.tudelft.nl/nw/users/vuik/papers/DUT-TWI-96-44.pdf].
 
  
−
При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким.  Вариант с частичной переортогонализацией является промежуточным.
+
* Преимуществом алгоритма является то, что он начинает поиск собственных значений матрицы начиная с максимального в абсолютном смысле значения. Это выгодно отличает данный алгоритм с точки зрения поиска собственных значений матрицы, находящихся по краям её спектра.
 +
* Вычислительная мощность алгоритма - отношение числа операций к суммарному объему входных и выходных данных - примерно равно <math>2k</math> при <math>k << n</math>
 +
* Алгоритм устойчив, так как операция переортогонализации как раз направлена на исключение проблемы округления вычисляемых значений
 +
* Алгоритм не является детерминированным, так как, во-первых, используется для разряженных матриц, и, во-вторых, является итерационным с выходом по точности - число операций заранее не определено
  
−
Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым.
+
= Программная реализация алгоритма =
  
−
== Программная реализация алгоритма==
+
== Особенности реализации последовательного алгоритма ==
−
=== Особенности реализации последовательного алгоритма===
 
−
=== Локальность данных и вычислений===
 
−
=== Возможные способы и особенности параллельной реализации алгоритма===
 
  
−
=== Масштабируемость алгоритма и его реализации ===
+
== Локальность данных и вычислений ==
−
Исследование масштабируемости реализации алгоритма проводилось с использованием стандарта MPI на суперкомпьютере "Ломоносов".
 
  
−
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:
+
== Возможные способы и особенности параллельной реализации алгоритма ==
−
*Число процессоров 4, 8, 16, 32, 64, 128.
 
−
*Размерность матрицы от 1000 до 50000
 
−
Сборка осуществлялась с параметрами:
 
−
*openmpi/1.5.5-icc
 
−
*intel/13.1.0
 
  
−
[[File:time_dependance.jpg| center|border |800px]]
+
== Масштабируемость алгоритма и его реализации ==
−
[http://pastebin.com/SbNrh7nz  Используемая параллельная реализация алгоритма на языке C++]
 
  
−
На данном графике отчетливо видно, что время выполнения алгоритма сильно уменьшается с увеличением количества процессов при расчете матрицы любой размерности. При этом наблюдается некоторое снижение производительности в случае наибольших размеров матриц. Данный факт является следствием большого количества данных, необходимого для обмена между процессами. Отсюда опытным путем можно установить, что наибольшая производительность алгоритма будет достигнута, если размерность матрицы не будет превышать 30000-35000.
+
Исследование масштабируемости алгоритма проводилось на суперкомпьютере [//hpc.cmc.msu.ru/ IBM Blue Gene/P ВМК МГУ.]
  
−
=== Динамические характеристики и эффективность реализации алгоритма===
+
Для компиляции программы использовались компиляторы intel/15.0.090 и  Openmpi/1.8.4-icc.
−
=== Выводы для классов архитектур===
+
 
−
=== Существующие реализации алгоритма===
+
Для проведения расчетов и получения полноценной картины поведения алгоритма в зависимости от входных данных и числа процессоров, программа была запущена на следующих параметрах:
 +
* в качестве размера входной матрицы подавались значения в диапазоне [2000:30000] c шагом 2000.
 +
* Число процессоров варьировалось от 1 до 256.
 +
Ниже на рисунке изображен трехмерный график, показывающий зависимость времени выполнения программы от входных данных/
 +
[[Файл:Lancos_SO.png|центр|мини|1000x1000пкс|График зависимости времени выполнения программы от входных данных]]
 +
[http://pastebin.com/SbNrh7nz ссылка код]
 +
 
 +
== Динамические характеристики и эффективность реализации алгоритма ==
 +
 
 +
== Выводы для классов архитектур ==
 +
 
 +
 
 +
== Существующие реализации алгоритма==
 
Алгоритм Ланцоша реализован в различных пакетах, библиотеках и проектах
 
Алгоритм Ланцоша реализован в различных пакетах, библиотеках и проектах
  
Строка 220: Строка 228:
 
Julia Math  https://github.com/JuliaMath/IterativeSolvers.jl Julia
 
Julia Math  https://github.com/JuliaMath/IterativeSolvers.jl Julia
  
−
==Литература ==
+
= Литература =
 +
 
 +
* Дж. Деммель, Вычислительная линейная алгебра. Теория и приложения. Пер. с англ. - М.: Мир, 2001.

Текущая версия на 16:07, 3 февраля 2017

Автор: Абдулпотиев А.А.



Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией
Последовательный алгоритм
Последовательная сложность [math]O(kn^2 + k^2n)[/math]
Объём входных данных [math]{n (n + 1) \over 2} + n + 1[/math]
Объём выходных данных [math]k + nk[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(kn + k^2)[/math]
Ширина ярусно-параллельной формы [math]O(n)[/math]


1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша это итерационный метод нахождения небольшого количества собственных значений столь больших разреженных симметричных матриц, что к ним нельзя применить прямые методы. Иными словами алгоритм сильно оптимизирует использование памяти и вычислительной мощности, что является критически важным для больших вычислений.

Сам алгоритм объединяет метод Ланцоша для построения крыловского подпространства с процедурой Рэлея-Ритца интерпретации собственных значений некоторой вычисляемой матрицы как приближений к собственным значениям исходной матрицы.

Пусть [math]Q = [Q_k,Q_u][/math] - ортогональная матрица порядка [math]n[/math], причем [math]Q_k[/math] и [math]Q_u[/math] имеют соответственно размеры [math]n \times k[/math] и [math]n \times (n-k)[/math]. Столбцы матрицы [math]Q_k[/math] вычисляются методом Ланцоша..

Запишем следующие соотношения:

[math]T = Q^T A Q = [Q_k, Q_u]^T A [Q_k, Q_u] = \left[ \begin{array}{cc} Q_k^T A Q_k & Q_k^T A Q_u\\ Q_u^T A Q_k & Q_u^T A Q_u \end{array} \right] = \left[ \begin{array}{cc} T_{k} & T_{ku}^T\\ T_{ku} & T_{u} \end{array} \right][/math]

Метод Рэлея-Ритца заключается в интерпретации собственных значений матрицы [math]T_k = Q_k^T A Q_k[/math] как приближенных к собственным значениям матрицы [math]A[/math]. Эти приближения называются числами Ритца. Если [math]A = V \Lambda V^T[/math] есть спектральное разложение матрицы [math]T_k[/math], то столбцы матрицы [math]Q_k V[/math] являются приближениями соответствующих собственных векторов и называются векторами Ритца.

Числа и векторы Ритца являются оптимальными приближениями к собственным значениям и собственным векторам матрицы [math]A[/math].

При применении метода Ланцоша в арифметике с плавающей точкой ортогональность в вычисленных векторах Ланцоша [math]q_k[/math] пропадает из-за ошибок округления. Потеря ортогональности не заставляет алгоритм вести себя совершенно не предсказуемым образом. В самом деле, мы увидим, что цена, которую мы платим за потерю, это приобретение повторных копий сошедшихся чисел Ритца. Для того чтобы поддержать взаимную ортогональность векторов Ланцоша, существуют две модификации алгоритма.

  1. Алгоритм Ланцоша с полной переортогонализацией. На каждой итерации запускается повторный процесс ортогонализации Грамма-Шмидта [math]z = z - \textstyle \sum_{i=1}^{j-1} (z^T q_i)q_i \displaystyle[/math]
  2. Алгоритм Ланцоша с выборочной ортогонализацией. Согласно теореме Пейджа векторы [math]q_k[/math] теряют ортогональность весьма систематическим образом, а именно, приобретая большие компоненты в направлениях уже сошедшихся векторов Ритца (Именно это приводит к появлению повторных копий сошедшихся чисел Ритца). Поэтому можно выборочно ортогонализировать векторы [math]q_k[/math] вместо того, чтобы на каждом шаге ортогонализировать вектор ко всем ранее сошедшимся векторам, как это делается при полной ортогонализации. Таким образом достигается (почти) ортогональности векторов Ланцоша, затрачивая очень небольшая дополнительную работу.

1.2 Математическое описание алгоритма

Пусть [math]A[/math] - заданная симметричная матрица, [math]b[/math] - вектор начального приближения метода Ланцоша. Тогда алгоритм Ланцоша вычисления собственных векторов и собственных значений матрицы [math]A[/math] с выборочной ортогонализацией имеет следующий вид:

[math] \begin{align} q_1 = & b / \Vert b \Vert_2, \; \beta_0 = 0,\; q_0 = 0\\ for \; & j = 1 \; to \; k \\ & z = A\,q_j\\ & \alpha_j = q_j^T z\\ & z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}\\ & for \; i=1 \; to \; k \\ & \; \; \; if \; \beta_k \|v_i (k)\| \le \sqrt{\epsilon} \Vert T_k \Vert_2 \; then\\ & \; \; \; \; \; \; z = z - (y_{i,k} ^ T z) y_{i,k} \;/*\; y_{i,k} = Q_k v_i \;*/ \\ & end \; for\\ & \beta_j = \Vert z \Vert_2\\ & if \; \beta_j = 0 \; then\\ & \; \; \; Stop\; the\; algorithm\\ & q_{j+1} = z / \beta_j\\ & /*Calculate\; eigenvalues\; and\; eigenvektors\; of\; T_j\; */\\ end \; & for \end{align} [/math]

Где [math]v_i[/math] - это столбцы ортогональной матрицы [math]V[/math] из спектрального разложения [math]T_k = V \Lambda V^T[/math], а [math]y_{k,i} = Q_k v_i[/math] - столбцы матрицы [math]Q_k V[/math] - векторы Ритца.

Матрица [math]T_j[/math]

[math] T_j = \begin{pmatrix} \alpha_1 & \beta_1 \\ \beta_1 & \alpha_2 & \beta_2 \\ & \beta_2 & \ddots & \ddots \\ & & \ddots & \ddots & \beta_{j-1} \\ & & & \beta_{j-1} & \alpha_j \end{pmatrix}\; [/math]


Согласно теореме Пейджа, [math]y_{k,i}^T q_{k+1} = O(\epsilon \Vert A \Vert_2) / \beta_k \Vert v_i(k) \Vert[/math], то есть компонента [math]y_{k,i}^T q_{k+1}[/math] вычисленного вектора Ланцоша [math]q_{k+1}[/math] в направлении вектора Ритца [math]y_{k,i} = Q_k v_i[/math] обратно пропорциональна величине [math]\beta_k \Vert v_i(k) \Vert[/math], являющейся оценкой погрешности для соответствующего числа Ритца. Поэтому, когда число Ритца сходится, а его оценка погрешности приближается к нулю, вектор Ланцоша приобретает большую компоненту в направлении вектора Ритца [math]q_{k,i}[/math], и следует произвести процедуру переортогонализации.

Величина погрешности [math]\beta_k \Vert v_i(k) \Vert[/math] считается малой, если она меньше, чем [math]\sqrt{\epsilon} \Vert A \Vert_2[/math], так как в этом случае, согласно теореме Пейджа, компонента [math]\Vert y_{i,k}^T q_{k+1} \Vert = \Vert y_{i,k}^T z \Vert / \Vert z \Vert_2[/math] скорее всего превосходит уровень [math]\sqrt{\epsilon}[/math] (на практике используется [math]\Vert T_k \Vert_2[/math] вместо [math]\Vert A \Vert_2[/math], так как первое известно, а второе не всегда).

1.3 Вычислительное ядро алгоритма

У описанного алгоритма два ядра, на которые приходится основное время работы алгоритма:

  • Вычисление вектора [math]z = A q_j[/math]
  • Выборочная переортогонализация [math]z = z - (y_{i,k} ^ T z) y_{i,k}[/math]

При больших [math]k[/math], сопоставимых с [math]n[/math] , к вычислительному ядру можно отнести вычисление собственных значений и собственных векторов трёхдиагональной матрицы. Однако на практике [math]k[/math] много меньше [math]n[/math].

1.4 Макроструктура алгоритма

Макроструктура алгоритма Ланцоша с выборочной переортогонализацией представляется в виде совокупности метода Ланцоша с выборочной переортогонализацией построения крыловского подпространства и процедуры Рэлея-Ритца.

Каждая итерация первого этапа может быть разложена на следующие макроединицы:

1 Умножение матрицы на вектор, [math]z=Aq_j[/math].

2. Вычисление вектора [math]q_{j+1} [/math] с помощью линейной комбинации других векторов:

[math]\alpha_j=q_j^Tz, [/math]

[math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, [/math]

[math]q_{j+1}=z/\|z\|_2[/math]

3. Ортогонализация вектора Ланцоша с помощью скалярного произведения:

[math]z = z-(y^T_{i,k},z)y_{i,k} [/math]

4. Нахождении собственных значений и собственных векторов матрицы и интерпретации их как приближенных значений собственных чисел и собственных векторов исходной матрицы, он может быть выполнен любым способом, например, разделяй и властвуй или же QR-итерацией.

1.5 Схема реализации последовательного алгоритма

На вход алгоритму подаются исходная матрица [math]A[/math], вектор начального приближения [math]b[/math] и число [math]k[/math]. Далее последовательно выполняются итерационно для всех [math]j: 1 \le j \le k[/math] следующие шаги:

  1. Умножается матрица на вектор для нахождения вектора [math]z[/math]
  2. Вычисляется коэффициент [math]\alpha_j[/math] посредством скалярного перемножения векторов
  3. Вычисляется новое значение вектора [math]z[/math]
  4. Производятся оценка погрешностей [math]\beta_k \Vert v_i(k) \Vert[/math] и выборочная переортогонализация
  5. Вычисление очередного значения [math]\beta_j[/math] - норма вектора [math]z[/math]
  6. Вычисление и добавление к матрице [math]Q[/math] нового столбца
  7. Вычисление собственных значений и собственных векторов матрицы [math]T_j[/math]

1.6 Последовательная сложность алгоритма

  • Вычисление вектора [math]z[/math] - [math]n^2[/math] операций умножения и [math]n(n-1)[/math] операций сложения
  • Вычисление скалярного произведения векторов - [math]n[/math] операций умножения и [math](n-1)[/math] сложений
  • Вычисление вектора [math]z[/math] - [math]2n[/math] умножений и [math]2n[/math] сложений
  • Оценка погрешностей - [math]kn[/math] операций умножения
  • Выборочная переортогонализация - [math]O(2nj)[/math] умножений и [math]O(2j(n-1) + n)[/math] сложений
  • Вычисление нормы вектора - [math]n[/math] операций умножения и [math](n-1)[/math] сложений
  • Вычисление нового столбца матрицы [math]Q[/math] - [math]n[/math] операций умножения

Итого на каждой итерации:

  • Умножений: [math]n^2 + n + 2n + kn + O(2nj) + n + n = n^2 + 5n + kn + O(2nj)[/math]
  • Сложений: [math]n(n-1) + n-1 + 2n + O(2j(n-1) + n) + n-1 = n^2 + 3n + O(2j(n-1) + n) -2[/math]

Итого за все время выполнения алгоритма:

  • Умножений: [math]kn^2 + 5kn + k^2n + O(k^2n + kn)[/math]
  • Сложений: [math]kn^2 + 3kn + O((k^2+k)(n-1)+kn) = kn^2 + 3kn + O(k^2(n-1)+2kn-k)[/math]

Суммарная последовательная сложность алгоритма - [math]O(kn^2 + k^2n)[/math].

1.7 Информационный граф

рис. 1: Информационный граф

1.8 Ресурс параллелизма алгоритма

Поскольку алгоритм является итерационным, то выполнять параллельные операции возможно только внутри каждой итерации алгоритма. Сами итерации выполняются в строгой последовательности и не могут быть параллелизованны:

  • Вычисление вектора [math]z[/math] - умножение матрицы размера [math]n \times n[/math] на вектор длины [math]n[/math] - [math]n[/math] ярусов сложений, [math]n[/math] операций умножений в каждом
  • Вычисление коэффициента [math]\alpha_j[/math] - скалярное произведение векторов - [math]n[/math] ярусов сложений, 1 операция умножения в каждом
  • Вычисление нового значения вектора [math]z[/math]: 2 яруса умножений длины [math]n[/math] (умножение вектора на число), 2 яруса вычитаний длины [math]n[/math]
  • Выборочная переортогонализация: последовательно для всех [math]i \le k[/math] выполняется [math]j[/math] ярусов сложений, [math]n[/math] операций умножений в каждом, [math]n[/math] ярусов сложений, [math]j[/math] операций умножений в каждом, один ярус вычитаний размера [math]n[/math]
  • Вычисление [math]\beta_j[/math] - скалярное произведение векторов - [math]n[/math] ярусов сложений, 1 операция умножения в каждом
  • Вычисление [math]q_j[/math] - деление вектора на число - один ярус делений размера [math]n[/math]

Сложность алгоритма по ширине ярусно параллельной формы - [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные

Вещественная матрица [math]A[/math] размера [math]n \times n[/math], вектор [math]b[/math] длины [math]n[/math], число [math]k[/math], но учитывая что матрица у нас симметричная количество входных данных можно уменьшить в два раза.

Объем входных данных: [math]{n (n + 1) \over 2} + n + 1[/math]

Выходные данные

Матрица собственных значений [math] \Lambda = diag(\theta_1 \dots \theta_k) [/math], матрица собственных векторов [math] V = [v_1 \dots v_k] [/math] размера [math] n \times k [/math]

Так, объем выходных данных: [math] k + kn [/math]

1.10 Свойства алгоритма

  • Преимуществом алгоритма является то, что он начинает поиск собственных значений матрицы начиная с максимального в абсолютном смысле значения. Это выгодно отличает данный алгоритм с точки зрения поиска собственных значений матрицы, находящихся по краям её спектра.
  • Вычислительная мощность алгоритма - отношение числа операций к суммарному объему входных и выходных данных - примерно равно [math]2k[/math] при [math]k \lt \lt n[/math]
  • Алгоритм устойчив, так как операция переортогонализации как раз направлена на исключение проблемы округления вычисляемых значений
  • Алгоритм не является детерминированным, так как, во-первых, используется для разряженных матриц, и, во-вторых, является итерационным с выходом по точности - число операций заранее не определено

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости алгоритма проводилось на суперкомпьютере IBM Blue Gene/P ВМК МГУ.

Для компиляции программы использовались компиляторы intel/15.0.090 и Openmpi/1.8.4-icc.

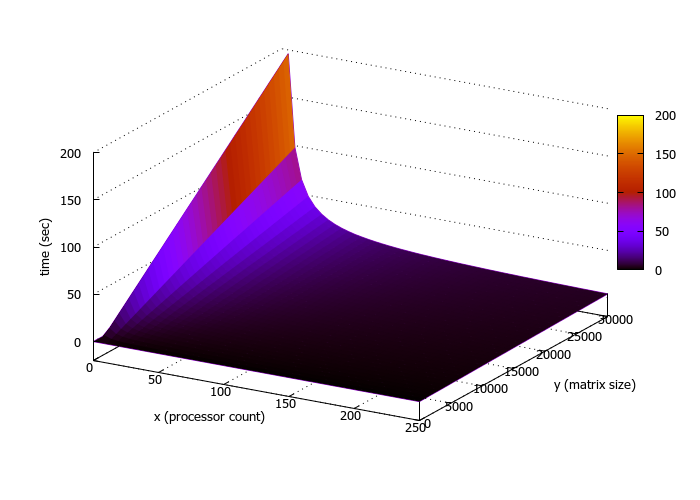
Для проведения расчетов и получения полноценной картины поведения алгоритма в зависимости от входных данных и числа процессоров, программа была запущена на следующих параметрах:

  • в качестве размера входной матрицы подавались значения в диапазоне [2000:30000] c шагом 2000.
  • Число процессоров варьировалось от 1 до 256.

Ниже на рисунке изображен трехмерный график, показывающий зависимость времени выполнения программы от входных данных/

График зависимости времени выполнения программы от входных данных

ссылка код

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Алгоритм Ланцоша реализован в различных пакетах, библиотеках и проектах

NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R

ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB

GrapLab https://turi.com/products/create/open_source.html C++

Gaussian Belief Propagation Matlab Package http://www.cs.cmu.edu/~bickson/gabp/ MATLAB

The IETL Project http://www.comp-phys.org/software/ietl/ C++

LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran

Julia Math https://github.com/JuliaMath/IterativeSolvers.jl Julia

3 Литература

  • Дж. Деммель, Вычислительная линейная алгебра. Теория и приложения. Пер. с англ. - М.: Мир, 2001.
Источник — https://algowiki-project.org/w/ru/index.php?title=Алгоритм_Ланцоша_для_арифметики_с_плавающей_точкой_с_выборочной_ортогонализацией&oldid=22070