Алгоритм Ланцоша с выборочной ортогонализацией

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Лáнцоша представляет собой мощный метод для нахождения нескольких собственных значений и собственных векторов симметричной матрицы А и для решения систем линейных уравнений. Алгоритм особенно эффективен, если матрица А разреженная и большого размера. Однако любая практическая реализация этого алгоритма страдает от ошибок округления, т.к. векторы Ланцоша теряют взаимную ортогональность. Для того чтобы поддерживать некоторый уровень ортогональности, появились методы полной переортогонализации и выборочной ортогонализации. В этой работе мы рассмотрим последний метод в качестве способа для поддержания ортогональности среди векторов Ланцоша. Он обладает почти столь же высокой точностью, как алгоритм с полной переортогонализацией, и почти столь же низкой стоимостью, как алгоритм без ортогонализации .

Дается вещественная симметричная матрица [math]A = A^T[/math],

[math] A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1\ n-1} & a_{1\ n} \\ a_{12} & a_{22} & a_{23} & \cdots & a_{2\ n-1} & a_{2\ n} \\ a_{13} & a_{23} & a_{33} & \cdots & a_{3\ n-1} & a_{3\ n} \\ \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ a_{1\ n-1} & \cdots & \cdots & a_{n-2\ n-1} & a_{n-1\ n-1} & a_{n-1\ n} \\ a_{1\ n} & \cdots & \cdots & a_{n-2\ n} & a_{n-1\ n} & a_{n\ n} \\ \end{pmatrix} [/math] [math] \, \; (1), [/math]

случайный вектор [math]b [/math], являющийся первым приближением собственного вектора матрицы, [math]k [/math] - количество собственных значений и собственных векторов, которые мы хотим найти, т.е. количество итераций.

На каждой итерации строится матрица [math]Q_j = [q_1, q_2, \dots, q_j][/math] размерности [math]n \times j[/math], состоящая из ортонормированных векторов Ланцоша [math]z[/math]. В качестве приближенных собственных значений берутся числа Ритца [math]\theta_i [/math], т.е. собственные значения симметричной трехдиагональной матрицы [math]T_j = Q^T_j A Q_j[/math] размерности [math]j \times j[/math].

[math] T_j = \begin{pmatrix} \alpha_1 & \beta_1 \\ \beta_1 & \alpha_2 & \beta_2 \\ & \beta_2 & \ddots & \ddots \\ & & \ddots & \ddots & \beta_{j-1} \\ & & & \beta_{j-1} & \alpha_j \end{pmatrix}\; (2). [/math]

Однако, векторы [math]q_j [/math] теряют ортогональность вследствие приобретения больших компонент в направлениях векторов Ритца [math]y_{i,j} = Q_j v_i [/math], отвечающих сошедшимся числам Ритца [math] \theta_i [/math]. Поэтому чтобы построить [math]q_j [/math], предлагается на каждом шаге следить за оценками погрешностей [math]\beta_{t}|v_i(t)|, i = 1 \dots t, t = j - 1 [/math], где [math]v_i(t) [/math] - [math]t[/math]-я компонента собственного вектора [math]v_i [/math]. И когда какая-то оценка становится слишком малой, проводить ортогонализацию вектора Ланцоша [math]z [/math]. Величина [math]\beta_{t}|v_i(t)| [/math] считается малой, если она меньше, чем [math]\sqrt{\varepsilon}||T_{t}|| [/math], где [math]\varepsilon[/math] - доступная машинная точность чисел.

После следует вычисление собственных значений [math] \theta_j [/math] и собственных векторов [math]v_j [/math] полученной трехдиагональной матрицы [math]T_j[/math], для чего существует, например, метод "разделяй и властвуй"

1.2 Математическое описание алгоритма

[math] \beta_0=0,q_0=0[/math]
[math] q_{1} = \frac{b_{j}}{\|b\|_2}[/math], где [math] \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2}[/math]
[math] for\, j=1\,\, to\, \, k\, \, do:[/math]
    [math]z=Aq_j,  [/math]
    [math]\alpha_j=q_j^Tz, [/math]
    [math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  [/math]
    [math]t = j - 1,  [/math]
    [math]for\, i=1\,\, to\, \, t\, \, do: [/math]
        [math]if\,  \beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \,  then:[/math]
            [math]z = z-(y^T_{i,t},z)y_{i,t} [/math], где [math]y_{i,t} = Q_{t}v_i[/math] 
    [math]\beta_{j}=\|z\|_2 [/math]
    [math]q_{j+1}=z/\beta_{j}, [/math]
    Строим матрицу  [math] T_j[/math] (2), вычисляем собственные значения  [math] \theta_j [/math] и собственные векторы [math]v_j [/math] полученной матрицы [math]T_j[/math].

1.3 Вычислительное ядро алгоритма

Выделены следующие вычислительные ядра:

• Умножение матрицы на вектор, [math]z=Aq_j, [/math].

• Ортогонализация по отношению к сошедшимся векторам [math]z = z-(y^T_{i,t},z)y_{i,t} [/math] для [math]i = 1 \dots t[/math]

1.4 Макроструктура алгоритма

Были выделены следующие макрооперации:

1. Умножение матрицы на вектор,

[math]z=Aq_j, [/math].

2. Вычисление вектора [math]q_{j+1} [/math] с помощью линейной комбинации других векторов:

[math]\alpha_j=q_j^Tz, [/math]

[math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1}, [/math]

[math]q_{j+1}=z/\|z\|_2[/math]

3. Ортогонализация вектора Ланцоша с помощью скалярного произведения:

[math]z = z-(y^T_{i,t},z)y_{i,t} [/math]

4. Для вычисления собственных значений матрицы будет использоваться алгоритм "разделяй и властвуй".

1.5 Схема реализации последовательного алгоритма

[math]1)[/math] Инициализируются векторы [math] \beta_0=0,q_0=0,[/math]
[math]2)[/math] Считается норма вектора [math] b: \; \;  \|b\|_2 = \sqrt{\sum\limits_{j=1}^{n} b_j^2},[/math]
[math]3)[/math] Находится первый вектор матрицы [math] Q: \; \; q_{1} = \frac{b_{j}}{\|b\|_2},[/math]
[math]4)[/math] Начинается цикл, повторяющийся [math] k [/math] раз по переменной [math] j: [/math]
   [math]4.1)[/math] Считается произведение матрицы на вектор: [math] z_d = \sum\limits_{y=1}^{n} a_{dy} q_{j_y}, \; d = 1,\,\dots\,, n, [/math] где 
   [math]z_d - [/math] компоненты вектора Ланцоша [math]z, [/math]
   [math]4.2)[/math] Скалярно умножается [math]q_j^T[/math]  и [math] z: \; \; \alpha_j = \sum\limits_{d=1}^{n}q_{j_d} z_d,[/math]
   [math]4.3)[/math] Вычисляется линейная комбинация векторов [math]z=z-\alpha_jq_j-\beta_{j-1}q_{j-1},  [/math]
   [math]4.4)[/math] [math]t[/math] Присваивается [math]j - 1.  [/math] В цикле по [math] i [/math] от первого до посчитанного [math] t[/math]-го собственного вектора проводится
   выборочная ортогонализация к сошедшимся векторам Ритца. То есть:
      [math]4.4.1)[/math] Считается норма матрицы [math]\|T_{t}\|_2, [/math] [math] \| T \|_2 =  \sup\limits_{\| x \|_2 = 1} \| T x \|_2 = \sup\limits_{(x, x) = 1} \sqrt{(Tx, Tx)}[/math], подчиненная векторной норме [math] \| x \|_2 = \sqrt{\sum_{i = 1}^n |x_i|^2} [/math]. Т.е. 
      [math] \|    T_{t} \|_2 =  \max\limits_{i=1 \dots t} \theta_i[/math], где [math] \theta_i[/math] - собственные значения матрицы [math] T,[/math]
      [math]4.4.2)[/math] Берется [math]t[/math]-ю координата вектора [math] v_i[/math]  и проверяется, выполняется ли равенство:[math]\beta_{t}|v_i(t)| \leqslant \sqrt{\varepsilon}\|T_{t}\| \, \, ,[/math]
      Если выполняется, то
          [math]4.4.2.1)[/math] Ищется вектор Ритца [math]y_{i,t_d} = \sum\limits_{x=1}^{t} q_{x_d} v_{i_x}, \; d = 1,\,\dots\,, n,[/math], где  [math]y_{i,t_d}[/math] -  [math]d[/math]-я компонента вектора Ритца [math]y,[/math]
          [math]4.4.2.2)[/math] Скалярно умножается [math]y_{i,t}^T[/math]  и [math] z: \; \; \gamma = \sum\limits_{d=1}^{n}y_{i,t_d} z_d,[/math]
          [math]4.4.2.3)[/math] Вычисляется линейная комбинация векторов [math]z = z-\gamma\,  y_{i,t}, [/math]
          [math]4.4.2.4)[/math] Увеличивается [math]i [/math]. Производится возврат к пункту [math]4.4.2,[/math]
   [math]4.5)[/math] Ищется норма вектора [math] z: \; \; \beta_{j}=\|z\|_2, [/math]
   [math]4.6)[/math] Ищется вектор Ланцоша [math]q_{j+1}=z/\beta_{j}, [/math]
   [math]4.7)[/math] Вычисляется новое собственное значение [math] \theta_j [/math] и собственный вектор [math] v_j [/math] для полученной матрицы [math] T_j,[/math]
   [math]4.8)[/math] Увеличивается [math] j [/math], производится возврат к шагу [math]4.1.[/math]

1.6 Последовательная сложность алгоритма

Рассмотрим последовательную сложность алгоритма.

[math]1)[/math] Инициализируются векторы,
[math]2)[/math] Считается норма вектора: [math] n [/math] сложений и умножений, одно вычисление корня,
[math]3)[/math] Находится первый вектор матрицы: [math] n [/math] делений,
[math]4)[/math] Начинается цикл, повторяющийся [math] k [/math] раз по переменной : [math]   j [/math]:
   [math]4.1)[/math] Считается произведение матрицы на вектор: [math]   n [/math] сложений и умножений,
   [math]4.2)[/math] Скалярно умножается два вектора : [math]   n [/math] сложений и умножений,
   [math]4.3)[/math] Вычисляется линейная комбинация векторов : [math]   2n [/math] вычитаний и умножений,
   [math]4.4)[/math] Повторяется цикл : [math]   j-1 [/math] раз. На каждом из этапов:
      [math]4.4.1)[/math] Считается норма матрицы: : [math]   j-1 [/math] сравнений,
      [math]4.4.2)[/math] Проверяется равенство::  2 умножения, одно сравнение
          [math]4.4.2.1)[/math] Ищется вектор Ритца : [math]   n*(j-1) [/math] сложений и умножений,
          [math]4.4.2.2)[/math] Скалярно умножаются два вектора:  [math]   n [/math] сложений и умножений,
          [math]4.4.2.3)[/math] Вычисляется линейная комбинация векторов : [math]   n [/math] умножений и вычитаний,
          [math]4.4.2.4)[/math] Увеличивается [math]i [/math]. Одно сложение.
     Таким образом, т.к. внутренний цикл повторяется [math]   j-1 [/math] раз, а [math]   j [/math] в свою очередь пробегает от [math]1 \dots k [/math], значит, полное количество операций в пункте [math]4.4)[/math], которое будет занимать весь внутренний цикл будет: сравнений [math] \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} [/math], умножений: [math] 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} [/math], сложений [math]\frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}[/math] и вычитаний [math] \frac{(n)k(k-1)}{2}[/math]
   [math]4.5)[/math] Ищется норма вектора: [math] n [/math] сложений и умножений
   [math]4.6)[/math] Ищется вектор Ланцоша [math] n [/math] делений
   [math]4.7)[/math] Увеличивается [math] j [/math], одно сложение. 
   
   Так, пункты  [math]4.1 - 4.3, 4.5 - 4.7[/math] занимают [math] k*(n+n+n+1)[/math] сложений, [math]k(n+n+2n+n)[/math] умножений, [math]2nk[/math] вычитаний и [math]n[/math] делений.



Подводя итог, общее количество операций умножения и деления [math]n + n + 2\frac{k(k-1)}{2}  + \frac{(k-1)k(k+1)}{3} + \frac{(2n)k(k-1)}{2} +  k(n+n+2n+n) + n[/math], т.е. [math]O( k^3+nk^2+k^2+kn+n )[/math]
общее количество сложений и вычитаний: [math] n + \frac{(k-1)k(k+1)}{3} + \frac{(n+1)k(k-1)}{2}+ \frac{(n)k(k-1)}{2} + k*(n+n+n+1) + 2nk[/math], т.е.  [math]O( k^3+nk^2+kn+n )[/math]
И [math] \frac{(k-1)k(k+1)}{3} + \frac{k(k-1)}{2} [/math] сравнений ( [math]O( k^3+k^2)[/math]).

1.7 Информационный граф

рис. 1: Информационный граф

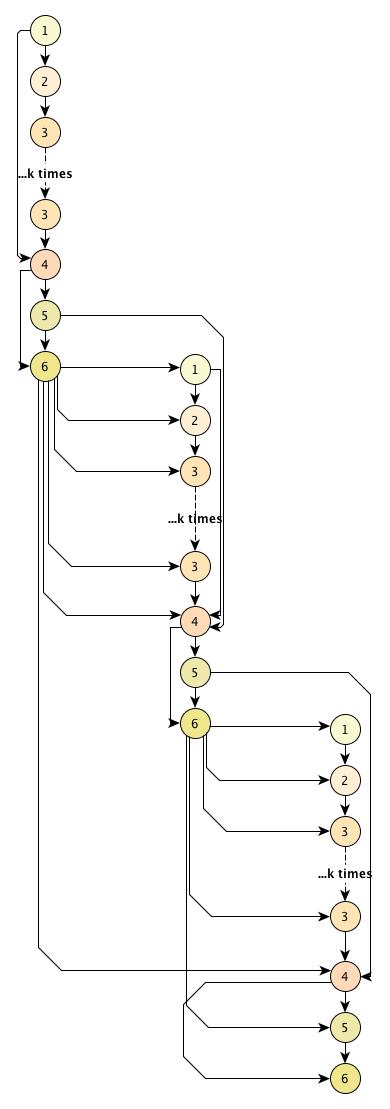
На рисунке (рис. 1) изображен информационный граф. Ниже приведено его описание:

• Вершины 1 соответствуют операции [math]Aq_j,[/math].
• Вершины 2 соответствуют операции скалярного произведения [math]q_j^Tz[/math].
• Вершины 3 соответствуют операции [math]z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i[/math].
• Вершины 4 соответствуют операции [math]z-\alpha_jq_j-\beta_{j-1}q_{j-1}[/math].
• Вершины 5 соответствуют операции [math]||z||[/math].
• Вершины 6 соответствуют операции [math]z/\beta_j[/math].

1.8 Ресурс параллелизма алгоритма

Хотя алгоритм является итерационным, возможно распараллелить внутри каждой итерации умножение матрицы на вектор и процесс переортогонализации Грамма-Шмидта.

Процесс умножения матриц matvec можно распараллелить несколькими способами[1].

Как видно из графа, для выполнения j-й операции, необходимо выполнить следующие ярусы:

1. [math]n[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом (вычисление [math]z[/math]);
2. [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\alpha_j[/math]);
3. [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (первая переортогонализация);
4. [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (вторая переортогонализация);
5. [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\beta_j[/math]);
6. [math]1[/math] ярус делений размера [math]n[/math] (вычисление [math]q_{j + 1}[/math]).

Если учесть весь ресурс параллелизма, можно получить мультипликативную вычислительную сложность всего алгоритма: [math]O(n^2k+nk^2)/p)[/math].

Вычислительная мощность данного алгоритма, как отношение числа операций к суммарному объему входных и выходных, данных равняется [math]O(k)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные

Матрица [math] A [/math], начальный вектор [math] b [/math] и число собственных значений, которые мы хотим найти [math] k [/math].

Ввиду симметричности из матрицы [math] A [/math] достаточно хранить только ее диагональ и элементы, лежащие выше ее. Таким образом, объем входных данных:

[math]\frac{n (n + 1)}{2} + n + 1 = \frac{n^2+3n+2}{2}.[/math]

Выходные данные

Матрица собственных значений [math] \Lambda = diag(\theta_1 \dots \theta_k) [/math], матрица собственных векторов [math] V = [v_1 \dots v_k] [/math] размера [math] n \times k [/math]

Так, объем выходных данных: [math] k + kn [/math]

1.10 Свойства алгоритма

Если [math]A[/math] эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам Ритца[2].

При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким. Вариант с частичной переортогонализацией является промежуточным.

Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

ЭТО

2.7 Существующие реализации алгоритма

Алгоритм Ланцоша реализован в различных пакетах, библиотеках и проектах

NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R

ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB

GrapLab https://turi.com/products/create/open_source.html C++

Gaussian Belief Propagation Matlab Package http://www.cs.cmu.edu/~bickson/gabp/ MATLAB

The IETL Project http://www.comp-phys.org/software/ietl/ C++

LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran

Julia Math https://github.com/JuliaMath/IterativeSolvers.jl Julia